小学6年生で解ける「面積の問題」、あなたは何分で解ける？

解説

それでは解説です。

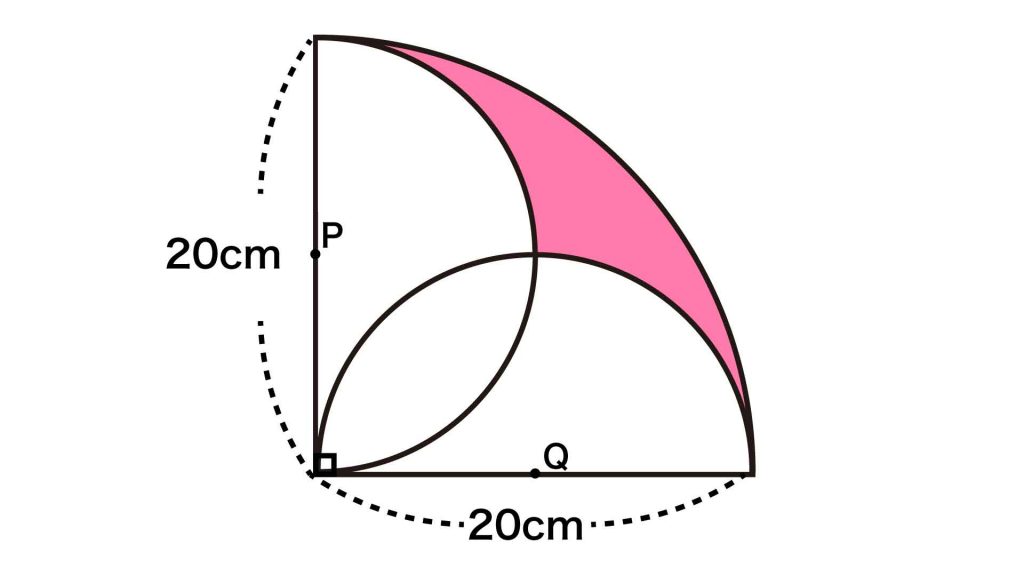
前ページ：【解答フォーム】自力で解きたい方はこちらへ！　以下は問題の答えです。

今回の問題の解き方をまとめた図がこちらです。ポイントは大きな扇形から面積を求めやすい図形を除くことです。

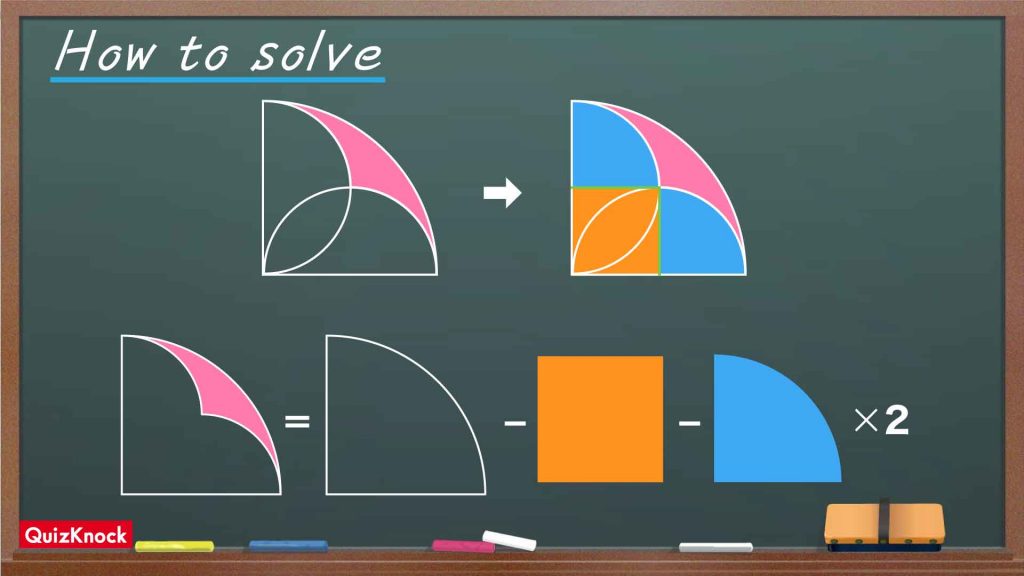
この図の流れに沿って、解いていきましょう！

補助線を引き、大きな扇形を分割する

まず、以下の図のように、点P、Qのそれぞれから2つの半円の交点に向けて補助線を引きます。

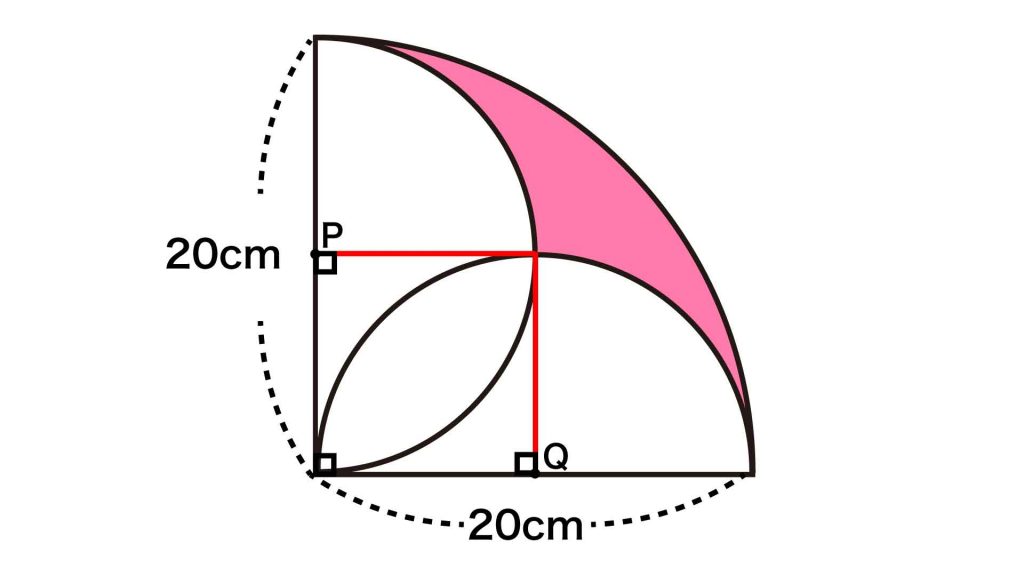
半径20cmの四分円（中心角が90度の扇形）は、以下の図のように、面積を求めたい赤い部分、1辺10cmの正方形、半径10cmの四分円2つに分割できます。

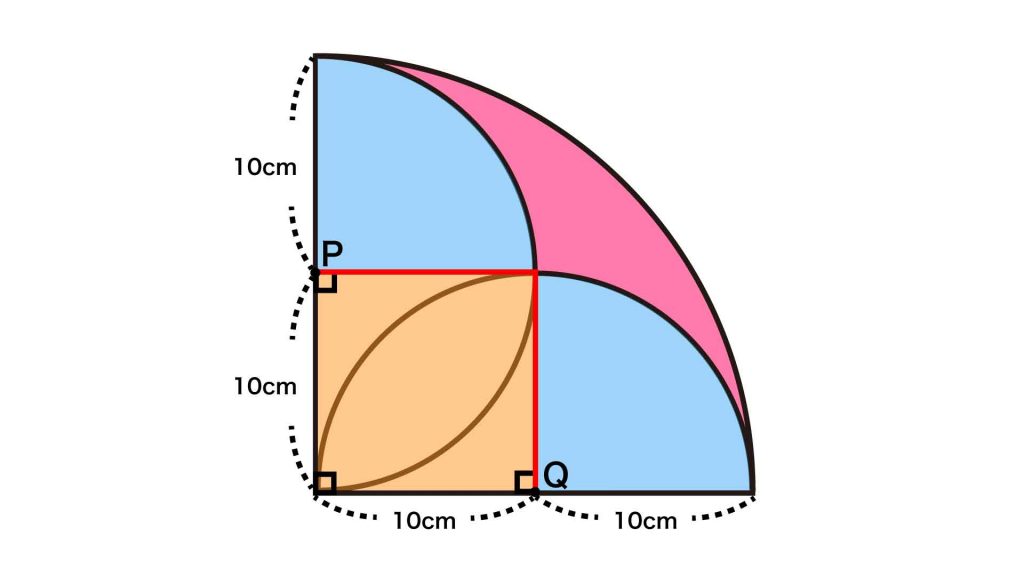
したがって、赤い部分の面積は、半径20cmの四分円の面積から、1辺10cmの正方形の面積と2つの半径10cmの四分円の面積を引くことで求めることができます。

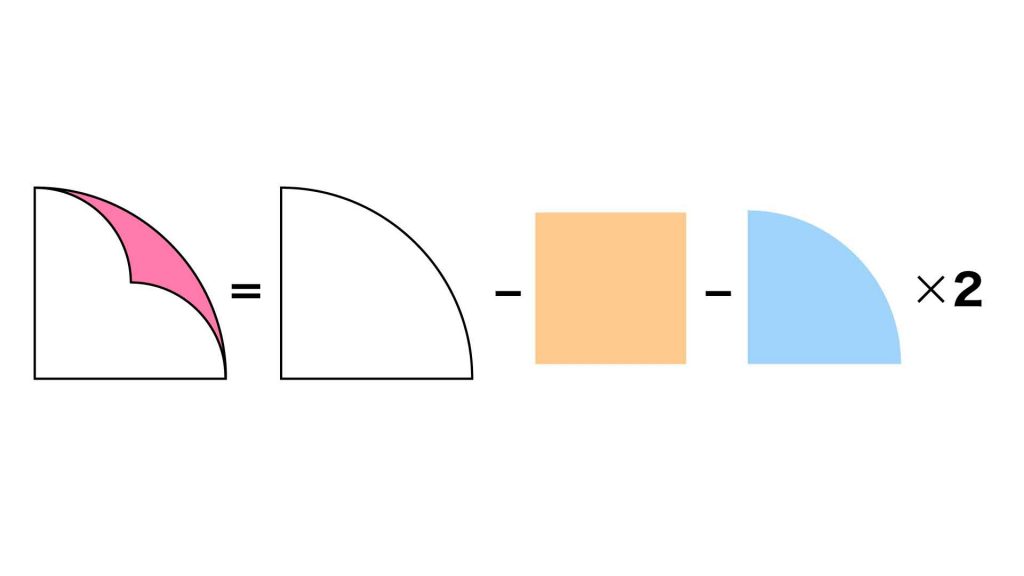
それぞれの面積を求める

赤い部分の面積を求めるために、半径20cmの四分円、1辺10cmの正方形、半径10cmの四分円の面積を求めましょう。

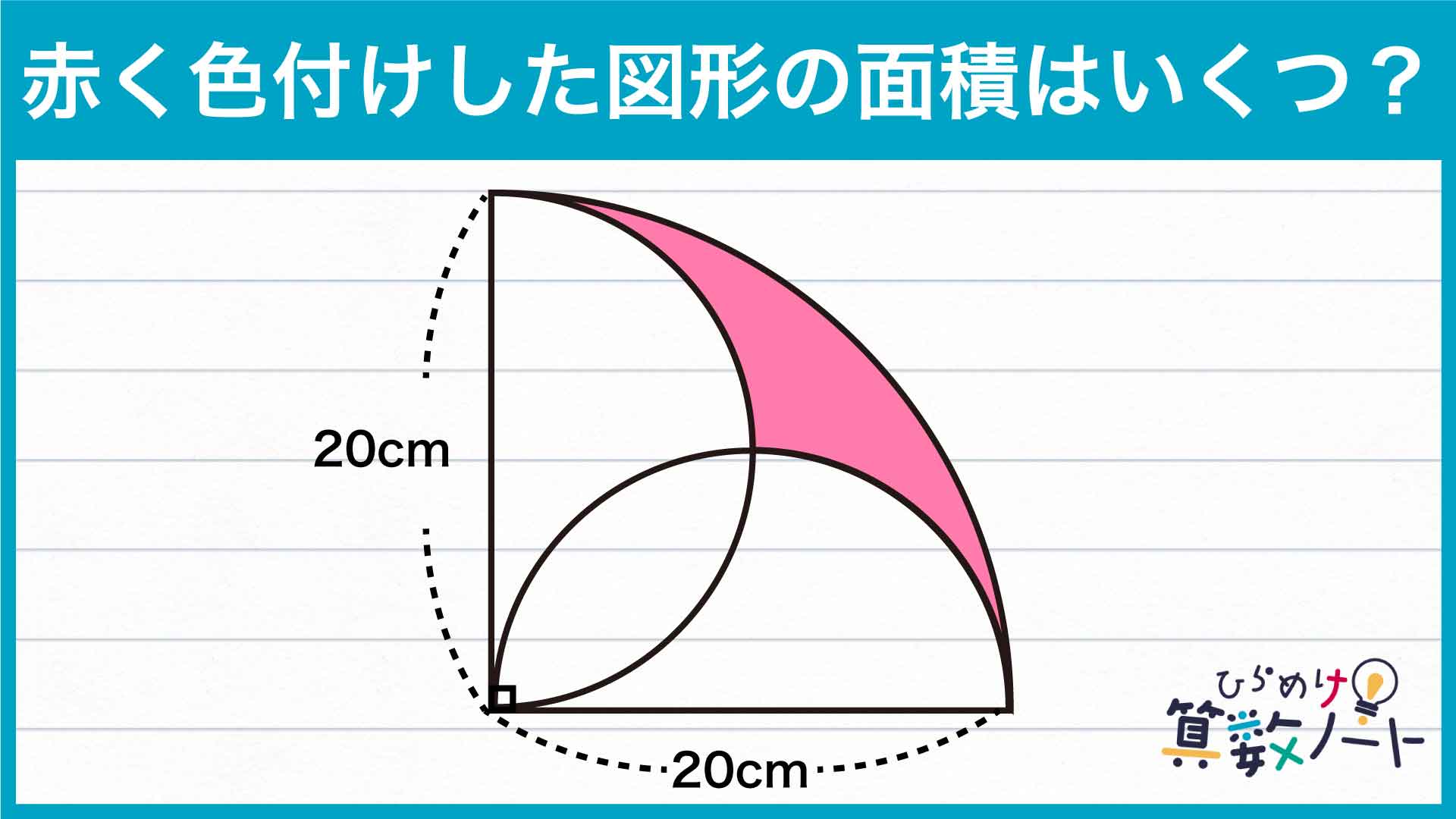
半径20cmの四分円の面積は、20×20×3.14÷4=314cm²となります。

1辺10cmの正方形の面積は10×10=100cm²、半径10cmの四分円の面積は10×10×3.14÷4=78.5cm²です。

あと一歩！

面積を求めたい赤い部分は、半径20cmの四分円から、1辺10cmの正方形と2つの半径10cmの四分円を除いた図形です。

したがって、求める面積は、314-100-78.5×2=57cm²となります。

答え：57cm²

「ひらめけ！算数ノート」のバックナンバーはこちら！

【前回の算数ノートはこちら】

【あわせて読みたい】