コジマです。
NISA制度の普及もあり、投資が数年前と比べて格段に身近になりました。最近積立を始めた、という方も多いのではないでしょうか。
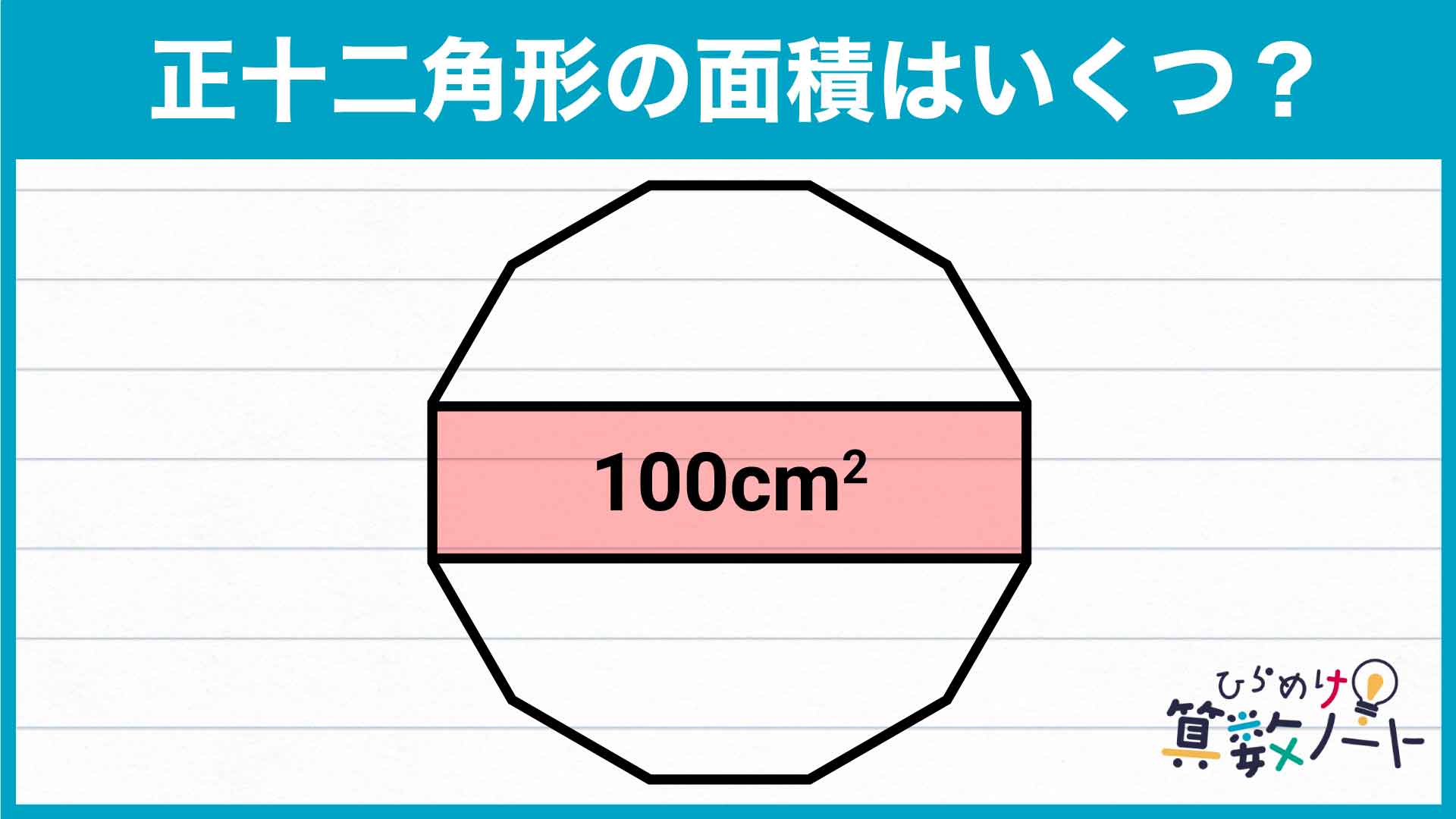
投資の勉強をしていると「72の法則」というものを聞いたことがあるかもしれません。72の法則とは「72を年利で割ると、元本が2倍になるまでのおおよその年数になる」という法則です。
例えば、年利4%の金融商品を100万円買ったとして、これが200万円になるまでどのくらい運用すればいいでしょうか? これを知りたいときに、72を年利の4で割ることで、おおよそ18年で2倍になることがわかるという訳ですね。
この法則、過去の投資家が経験則によって編み出したもの……という訳ではなく、きちんと数学的な根拠があります。高校数学レベルの知識があれば十分理解できる内容ですので、あのとき習ったことを思い出しながら導出の過程を追ってみましょう。
(※前提として、この記事で扱う利率はすべて複利法で考えることとします)
目次
* * *

正攻法の説明
まず「年利」について改めて確認しておきます。年利がr(パーセント表記で100r%)の金融商品を買ったとき、1年後には元本のr倍の利息がつきます。このとき、利息は翌年の元本へ繰り越され、元本は1年後に(1+r)倍になります。
複利法では、2年後には(1+r)倍になった元本がさらに(1+r)倍になるので、元本は2年で(1+r)2倍になります。同様に3年後は(1+r)3倍、4年後は(1+r)4倍ですね。
元本が2倍になるまでの年数を考える訳なので、年数をnと置いて立式してみましょう。n年後に元本が2倍になるとき、nとrの間に次のような関係が成立します。

この式の左辺は指数関数になっていてこのままだと扱いづらいですが、こういうときは対数の出番です。両辺の自然対数をとって(この記事では自然対数の底eは省略します)、対数関数内の指数を外に出して変形することで、nについての式を得ることができます。

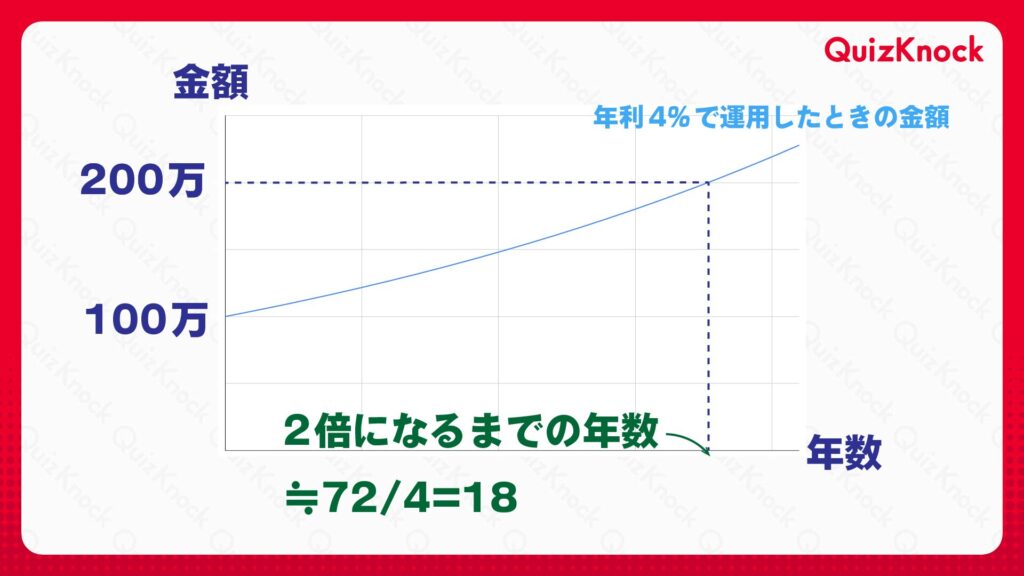
この右辺は分母に対数関数が入っていてあまり簡単に計算できそうにないですが、大学レベルの数学で学ぶマクローリン展開という方法を使うと、実は分母はrが0に近い場合はrで近似できるということがわかります。

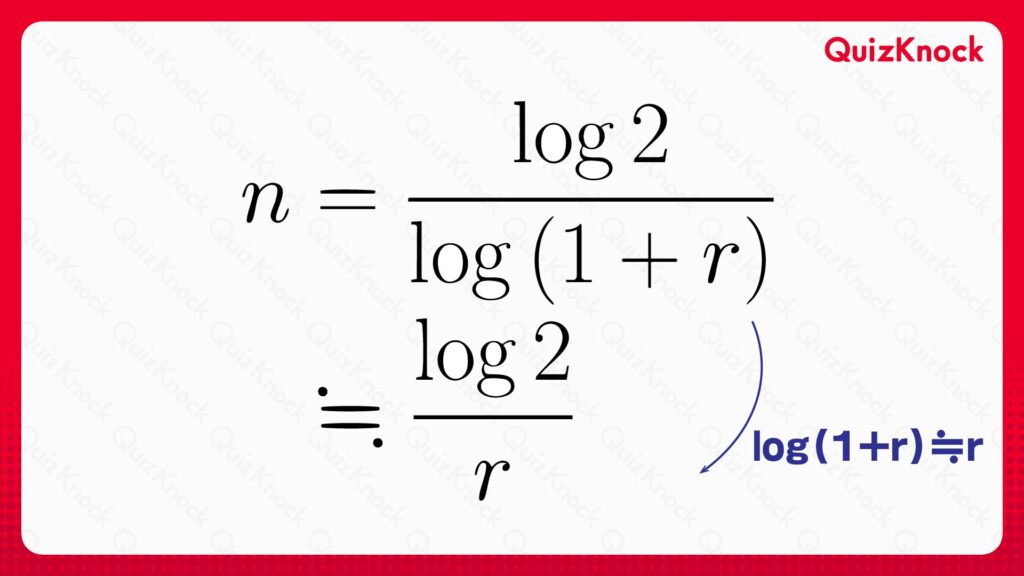
これで、n≒log2/rであることがわかりました。年利rは割合であること(パーセント表記の場合は100をかける必要があること)、2の自然対数は0.693...であることに注意すると、以下のように69を年利で割ると2倍になるまでの年数が求められることがわかります。

……え、69やんけ。72はどこに行った?
実は、72よりも69を使ったほうが実際の年数に近い値を求めることができます。しかしこの法則の意義は「元本が2倍になるまでのおおまかな年数が簡単な計算でわかること」です。年利は1%から10%までの整数であることが多いため、そのうち5と7以外で割り切れる72が69の代わりに用いられています。利便性優先ということですね。
高校生でもわかるように説明できないか?
72の法則を確かめる目的であればここまでの説明で十分です。ただ、マクローリン展開を利用した近似が登場するため、大学数学を通っていないと納得感が薄いかもしれません。
そこで、今回は高校数学の範囲で72の法則が成り立つことを確かめてみましょう。

先程の説明では最初に対数をとりましたが、この方針だとマクローリン展開を使わないと結論に辿り着けません。今度は、累乗の式を展開するときに便利な二項定理を使ってみましょう。
二項定理は次のような式で表されます。式にするとややこしいですが、要は(x+1)2=x2+2x+1や(x+1)3=x3+3x2+3x+1の指数に関する一般化です。

これを用いると、最初の式が次のように展開できます。

・・・で省略されている部分はrの3次以上の(=rを3以上で累乗している)項です。rは年利で大抵は0.1以下ですから、3乗すると非常に小さくなるので無視してしまっていいでしょう。
これをnについて整理します。

だいぶ見通しが良くなってきました。rnをxと置くとさらに簡単な式に変形できそうですが、(2-r)の部分がややネックですね。
先程、rは年利だから大抵は0.1以下と書きました。つまり、2-rのrが無かったとしても1.9が2になるくらいの違いしかありません。今回はこのrを無視することにします。
(※「1.9が2になるくらいの違い」は無条件で無視していい大きさではないのですが、今回は計算の精度がそれほど重要でないケースなので無視しています)

何ということでしょう。複雑な数式が100万回解いてきた簡単な二次方程式に様変わり。
もう勝ったも同然です。解の公式を使って解くとx=-1±√3となりますが、x (=rn) は「年利と年数の積」なので正の値になるはずです。よってこのプラスマイナスはプラスしかあり得ず、

めでたくnが綺麗な形で求められました。ルート3の値は覚えている人も多いでしょう。「人並みに奢れや」で1.73……ですね。
マクローリン展開で導出したときと同様に、パーセント表記の年利で割りたいので分母と分子に100をかける必要があります。以下のように計算することで、年利で73を割ると2倍になるまでの年数が求められるという結論を得ることができました。

近似の影響で誤差は大きくなりますが、72辺りの整数を分子にすると2倍になるまでの年数が求められることが確かめられました。ルート3の小数部分が72に繋がるのが面白いですね。
まとめ
投資の世界でよく知られる「72の法則」を数学的に確かめる方法を2パターン紹介しました。
大学入試にも生かせるテクニックがいくつか含まれているので、受験勉強の合間に頭の体操でやってみるのもいいかもしれません。また、元本が2倍になるまでの年数ではなく、1.5倍など他の倍率でも(結果が綺麗になるかはともかく)同様に求められます。興味がある方はお試しあれ。










.jpg)