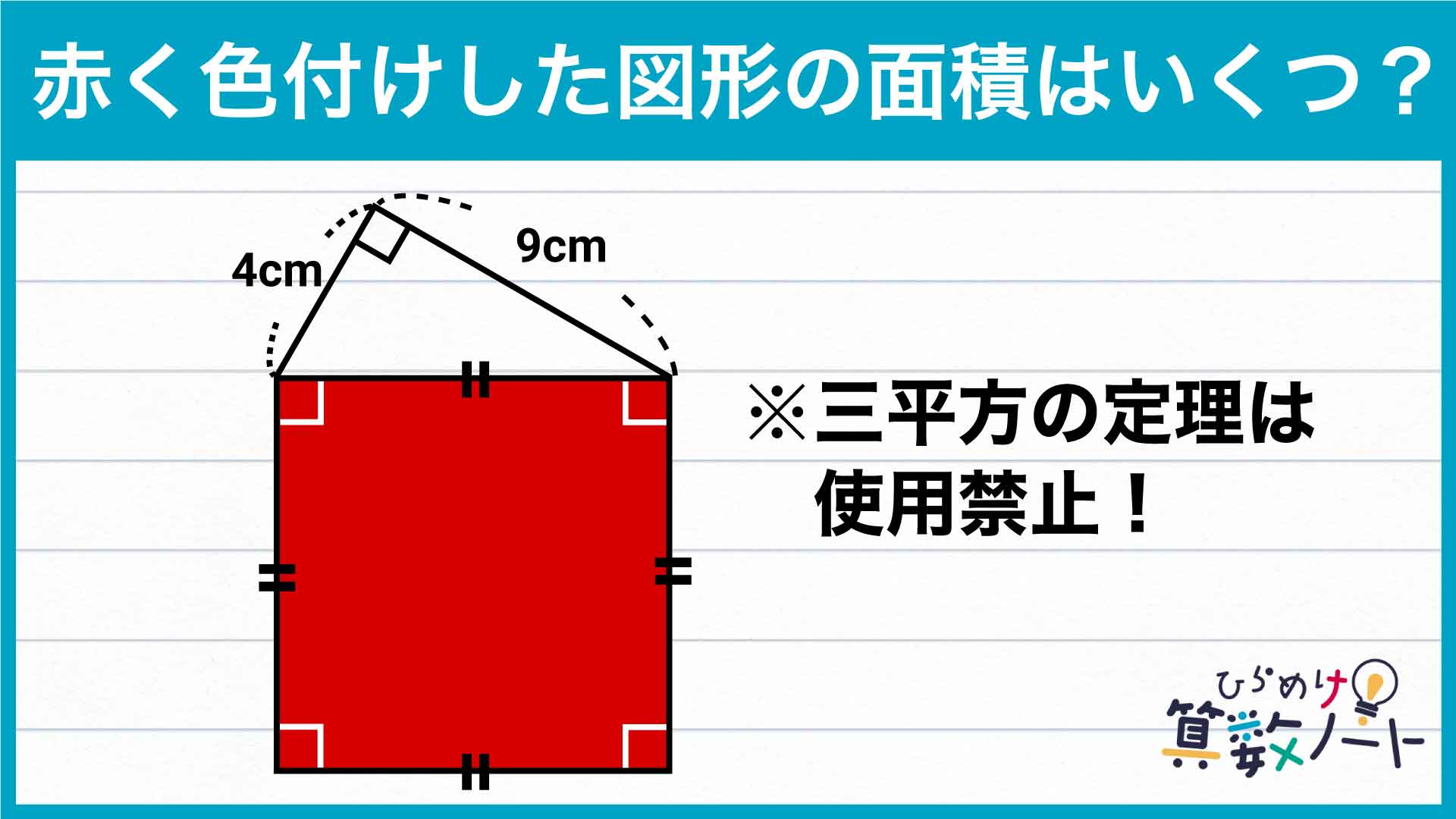
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
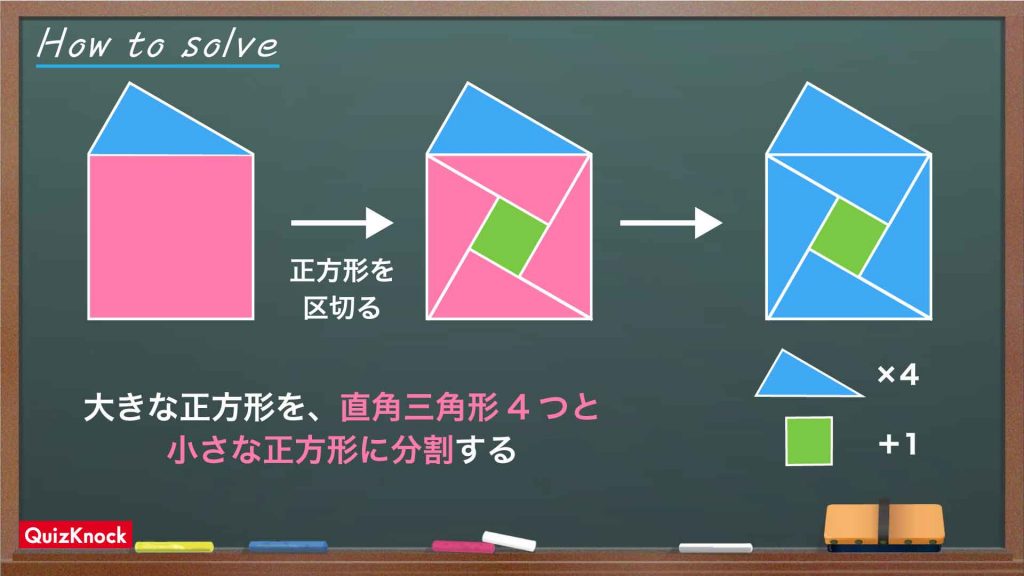
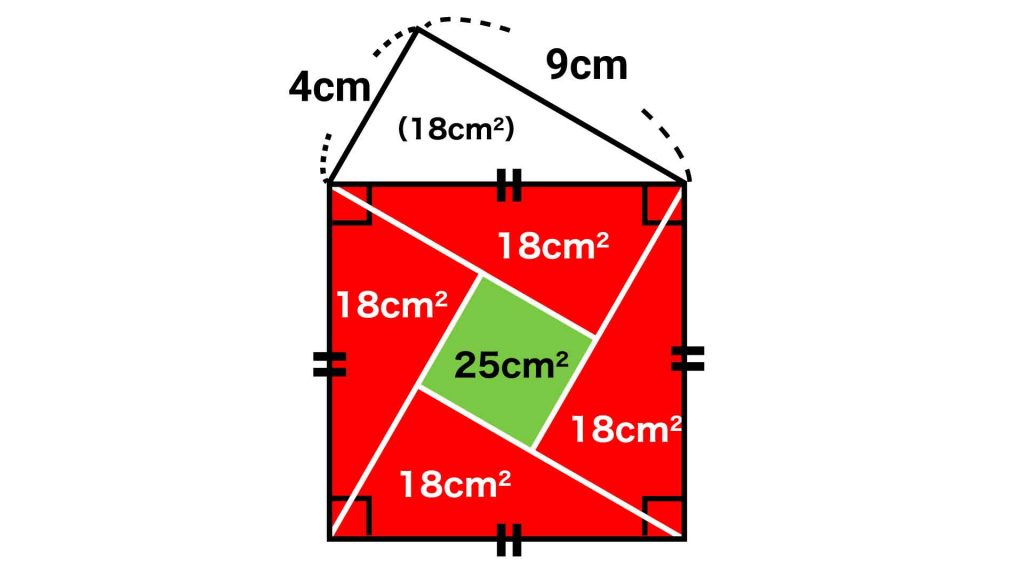
ポイントは、正方形を直角三角形4つと小さな正方形に区切って考えることです。
では、この流れに沿って解いていきましょう!
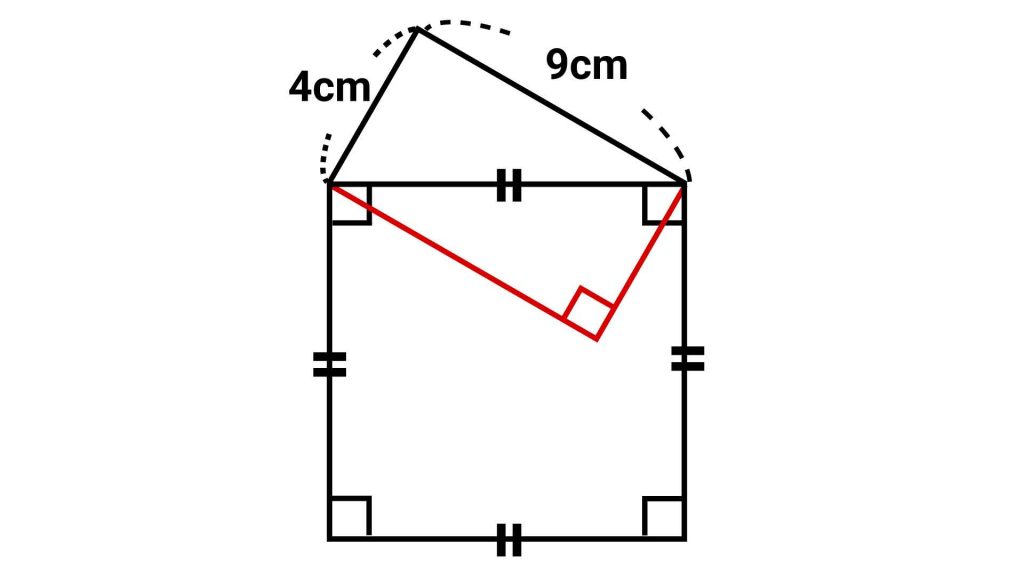
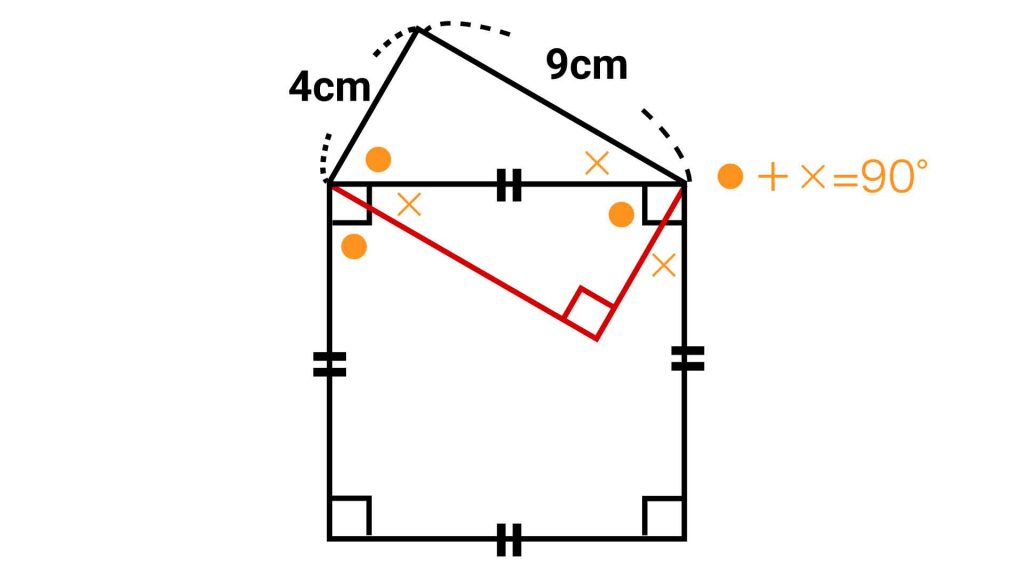
外にあった直角三角形を……
正方形の上に乗っていたのと同じ直角三角形を、正方形の中に入れてみます。
三角形の内角の和は180度なので、〇と×で表された角の大きさの合計は180-90=90度です。正方形の内角もそれぞれ90度なので、図のように新しく〇や×で表せる角度ができました。
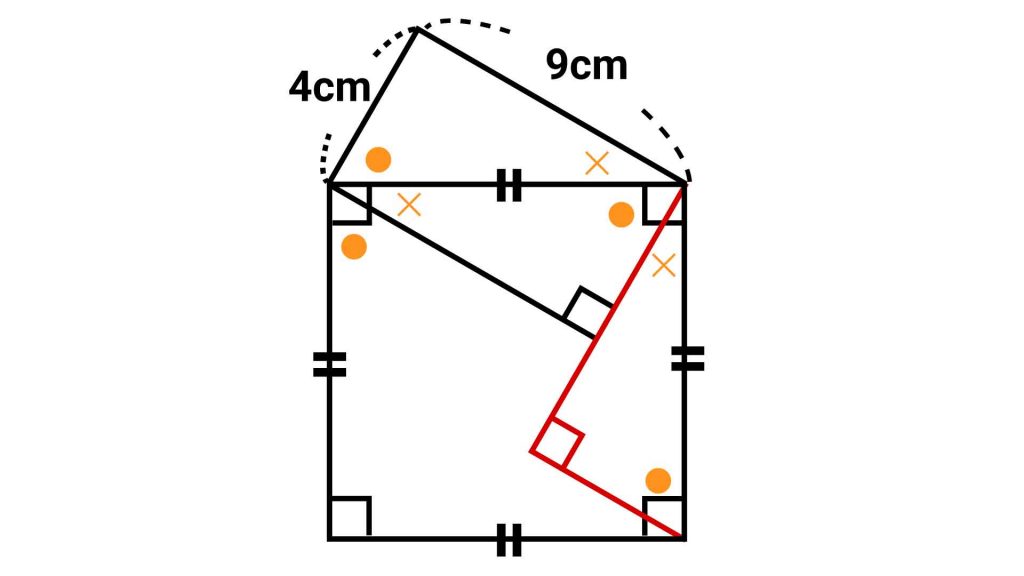
もっと敷き詰めてみる
同じ直角三角形をもう1つ追加してみましょう。正方形の一辺と斜辺の長さが同じなので、ちょうど×の角の部分にすっぽり当てはめることができます。
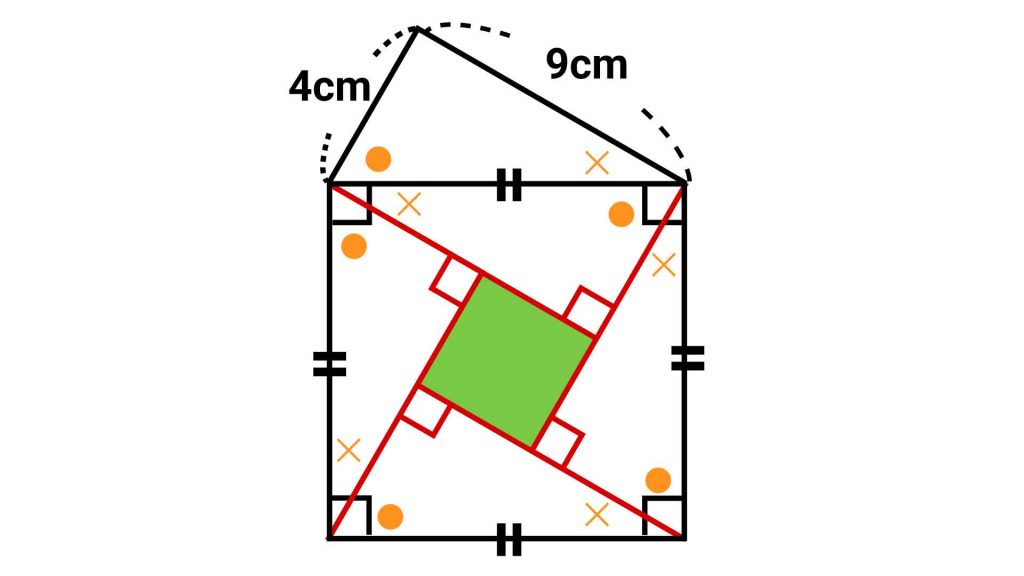
同じようにして、正方形の中に4個の直角三角形を描くことができます。真ん中には小さな正方形ができました。
面積の合計を求める
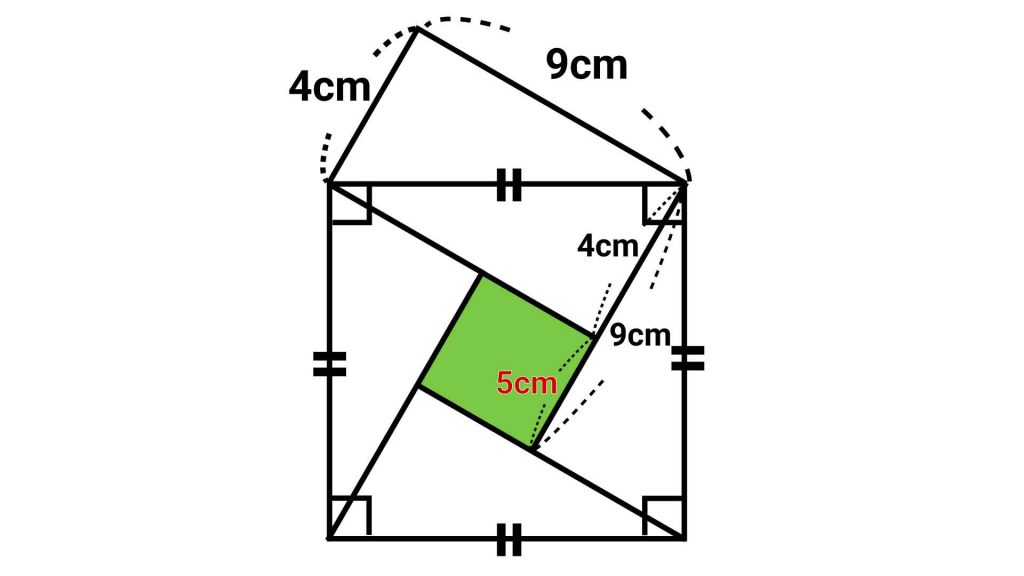
小さな正方形の一辺は、直角三角形の辺の差から9-4=5cmと求めることができます。
最後に、それぞれの図形の面積を求めます。
大きな正方形の一部を構成する4つの直角三角形の面積は、すべて4×9÷2=18cm²、中央にできた正方形の面積は、5×5=25cm²です。
したがって求める面積は、4つの直角三角形と1つの正方形の面積を合計して18×4+25=97cm²とわかります。
答え:97cm²
三平方の定理を使うと瞬殺できる!
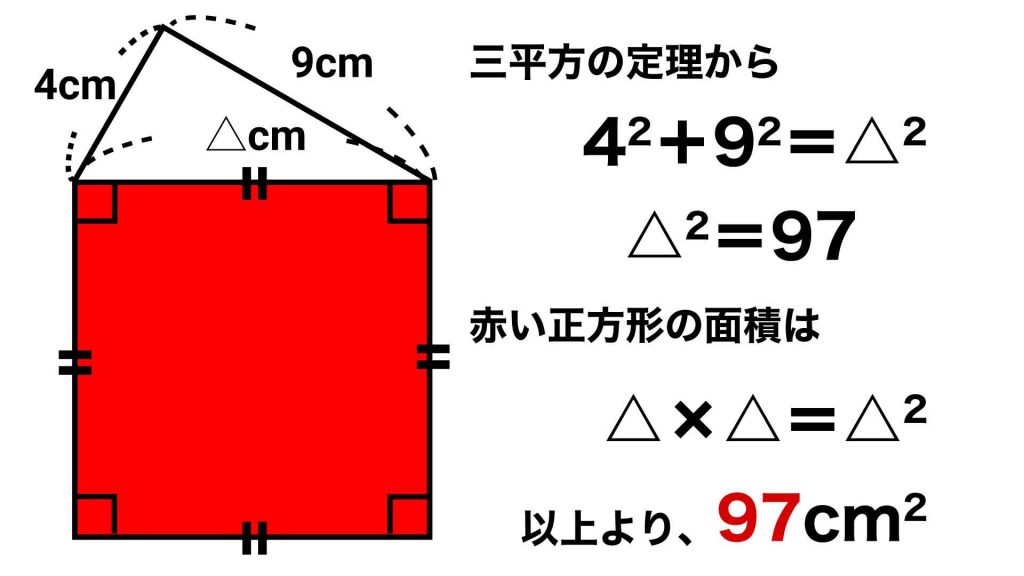
ちなみに、中学校で習う「三平方の定理」を使うと、
求める正方形の面積=(直角三角形の斜辺の長さ)²=(斜辺を除く各辺の長さ)²の合計
ということから、正方形の面積は4²+9²=97cm²であると簡単にわかります。
これに比べれば、直角三角形を敷き詰めて解く方法はずいぶんややこしく見えますが、実はひらめき次第で中学校の学習内容を使わなくても解ける問題だったのです。
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)

















