Happy birthday to you! ナイスガイの須貝です。
今日も誰かの誕生日ですね……ということで誕生日にまつわるお話!
クラスに誕生日同じヤツ絶対いる説
君たちは聞いたことがあるだろうか……。「1つのクラスに必ず同じ誕生日の人が1組以上いる」という噂を……。
うるう年の2月29日生まれの人もいるとして、一年は366日、クラスは40人。本当に同じ誕生日のヤツがいるのか……?
自分のクラスを思い出してみると、確かにいたなぁ、という感想。みなさんのクラスはどうですか?いますか?
余事象の確率
じゃあこの問題を考えてみましょう。もちろん確率の問題です。求めたいのは「40人のクラスに誕生日が同じ人がいる確率」。日付が366日でクラスが40人だから40/366、とはならないのがこの問題。
この問題を解くためのポイントは問題の言い換え!求める確率を「40人のクラスで誕生日が同じ人がいない確率を1から引いたもの」と考えるのです。
同じ誕生日になる確率とだけ言うと、同じ日に3人が被っている場合や誕生日が同じペアが2組ある場合などとても多くの場合を考えなければなりません。しかし、余事象(知りたい出来事の反対の出来事のこと)の確率の考え方を使えば、全員が別の誕生日である確率を求めるだけでよいのです。
計算
それでは実際に「40人のクラスに誕生日が同じ人がいない確率」を計算してみましょう。うるう年生まれの学年のクラスで確率を計算することにします。
まず1人目は366日のうちどの日付でもよいので、366/366 = 1 。つまり、1人のクラスだと誕生日が同じ人がいない確率は1(全員の誕生日が違う)ということです。当たり前。
2人目は1人目と違う日付です。すなわち、2人目の誕生日は366通りのうち、1人目の日付を除いた365通りしかありません。今、1人目と2人目の誕生日の選び方に同じ日付を選ばない以上の関係はないので、確率は掛け算することができます。したがって、2人の誕生日が違う確率は、366/366 × 365/366 = 0.997 。99.7%の確率で2人の誕生日は違います。そうだろうね。
3人目も同じく、1人目、2人目と違う日付を選んで、2人の誕生日が違う確率に掛け算します。よって、366/366 × 365/366 × 364/366 = 0.992 。99.2%の確率で3人の誕生日は違うというわけです。
この調子で40人まで進んでいきましょう。計算は電卓で順番にやればよし!ただ、こういうときのためのExcelって感じもするのでExcelを使いますか。同じ計算を繰り返すときはドラッグしてビーッと引っ張ると勝手にやってくれて便利です。計算結果は以下の通り。
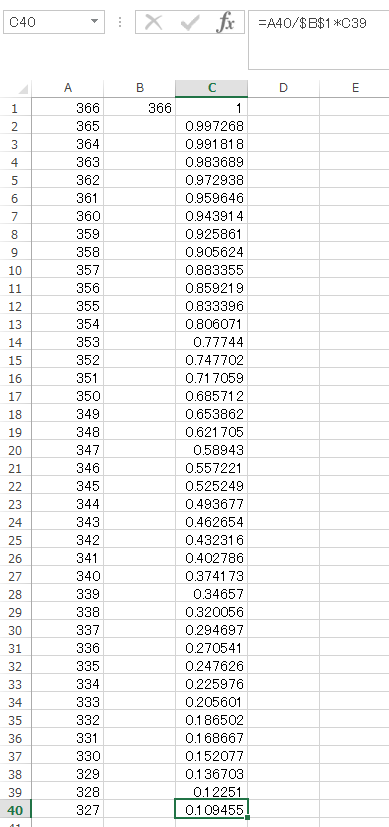
一番左の数字がクラスの人数です。A列はみんな誕生日が被っていないとして残っている日付の個数です。B列は分母の366。いっぱい書くと大変なので1個だけにしちゃいました。C列が計算結果です。n人目の誕生日を選ぶ確率(A列/B列)を一つ上の計算結果に掛け算したものを表示しています。(画像右上の式参照)
40人クラスになると誕生日が同じ人がいない確率は10.9%まで落ちるのです!
したがって、40人クラスに誕生日が同じ人がいる確率は、1 - 0.109 = 0.891 。ということで、89.1%でした。
ちなみに、1年が365日だとして同じ計算をしても、誕生日が同じ人がいない確率は 10.9%になります。(小数第2位を四捨五入)
まとめ
9割近い確率でクラスの中に同じ誕生日の人がいるんですね。説はほぼ正しい!
追記
この記事に色々な反応を頂きました!その中に「私と同じ誕生日の人がいたことはないですね。」のようなコメントもありました。
確かに、自分と同じ誕生日の人がいた、という人は少ないのかもしれません。90%の確率で誕生日が同じ人同士がいるはずなのに、自分と同じ誕生日がいた記憶はない……。それも不思議ですね。
というわけで、自分と同じ誕生日の人がいる確率も調べてみましょう!
これも同じく、自分(特定の1人)と同じ誕生日の人がいない確率を計算します。1人目の誕生日の選び方は366日。次の人からは「1人目と同じ誕生日を選ばない確率」なので、ずっと 365/366 を掛け続けるだけ!計算結果は以下の通り。
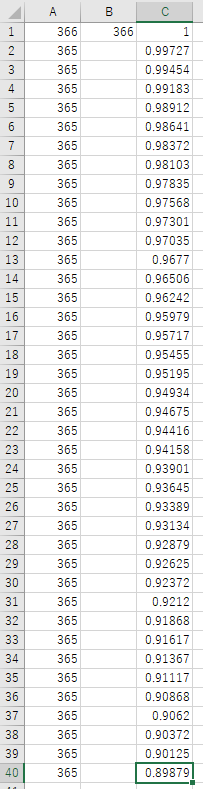
40人クラスで自分(特定の1人)と同じ誕生日の人がいない確率は89.9%なんですね。ちなみに1年を365日で計算しても89.9%です。
すなわち、自分と同じ誕生日の人がいる確率は 1 - 0.899 = 0.101で、10.1 %でした。これは自分と同じ誕生日の人がいないと感じるのも納得の数字ですね。









.jpg)