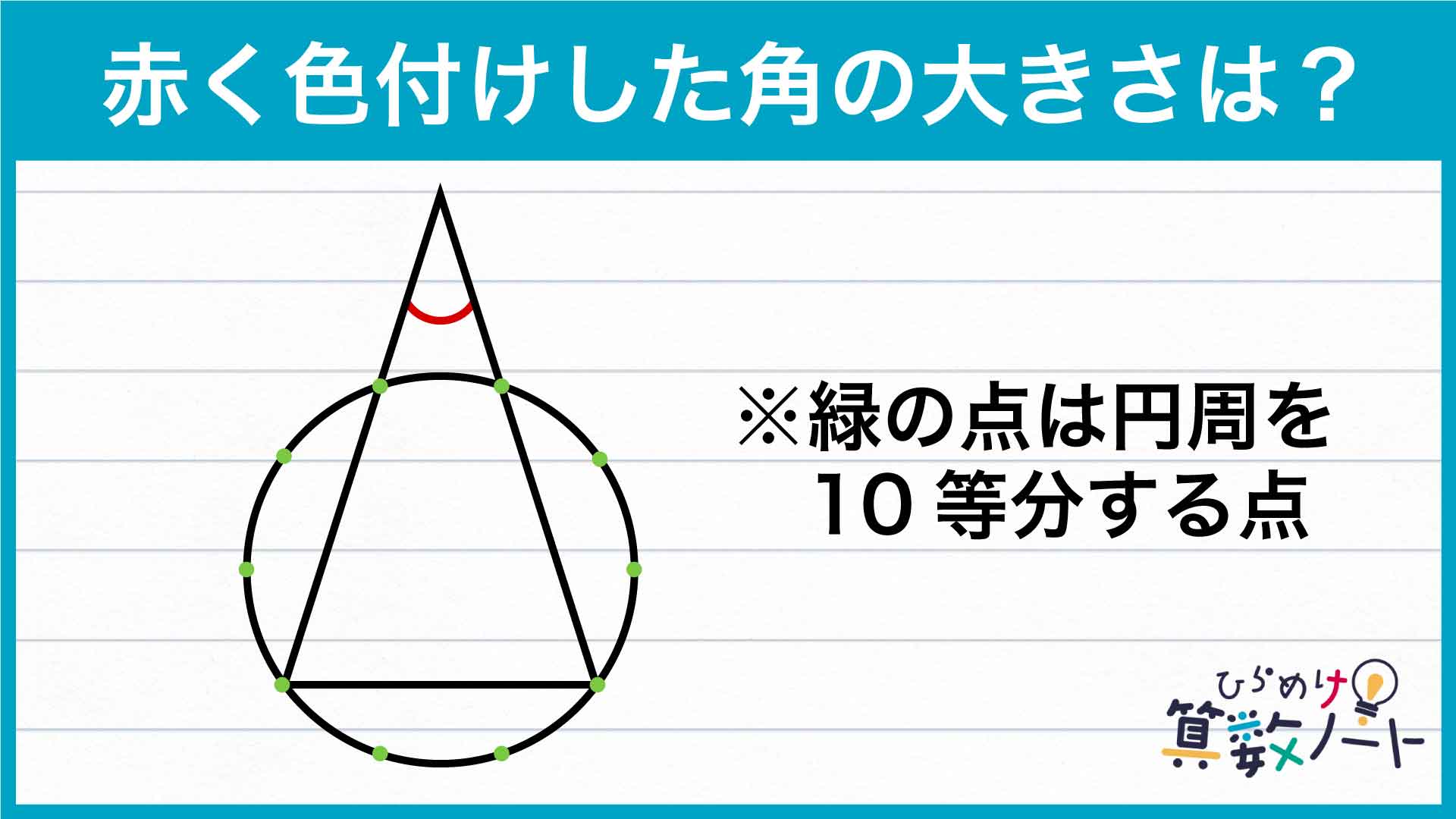
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
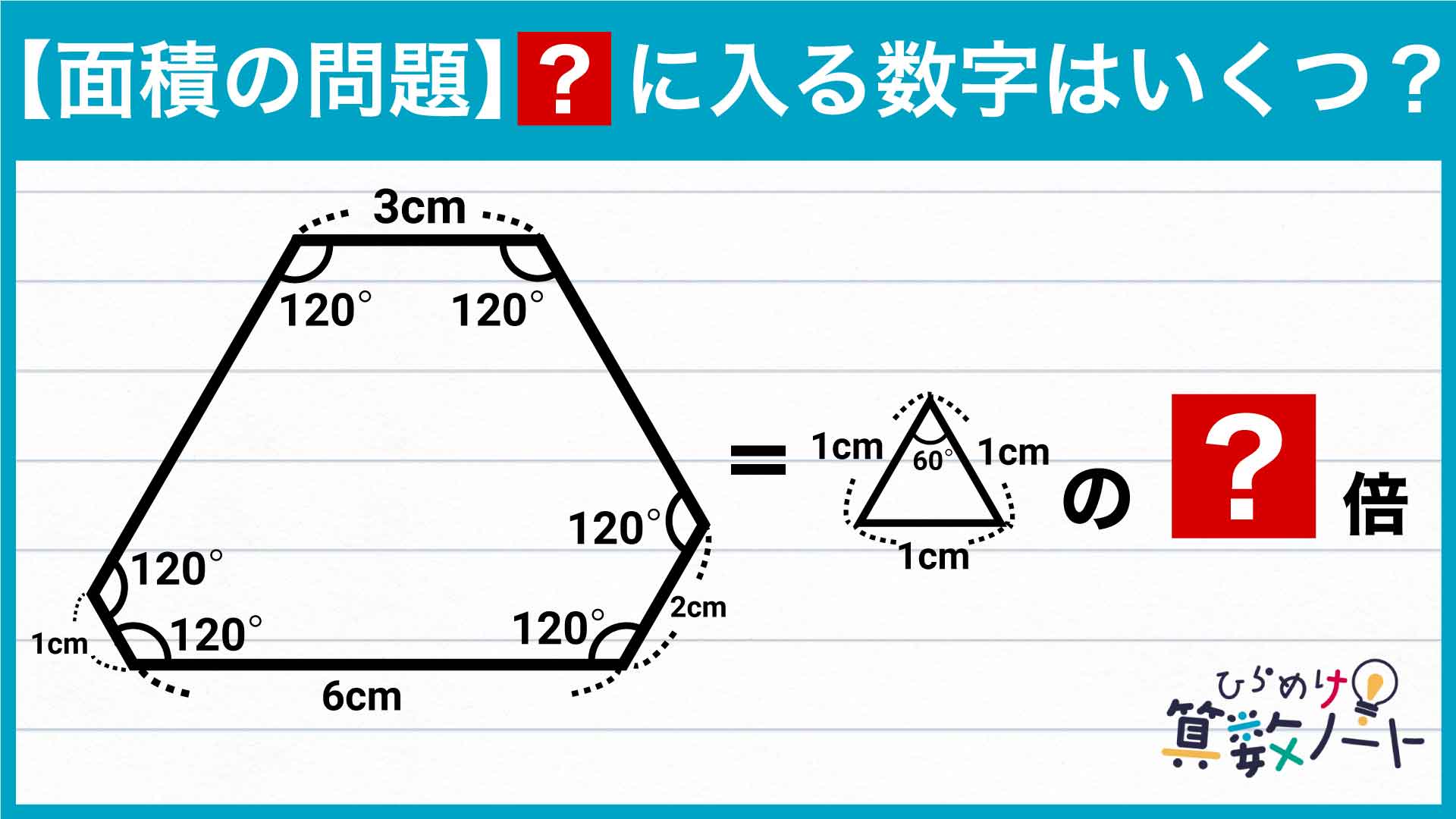
今回のポイントをまとめた図がこちらです。
求めるのは「六角形の面積が、一辺の長さが1cmの正三角形の面積の何倍か」なので、設問の六角形のままでは答えを導くのが難しそうです。
そこでポイントになるのは、補助線を引いて六角形を大きな正三角形に変えること。そうすると、大きな正三角形だけでなく、いろいろな大きさの正三角形ができます。そしてそれぞれの正三角形が、一辺の長さが1cmの正三角形何個分であるかを求めることができれば、足し引きによって答えを導くことができます。
それではこの流れに沿って解いていきましょう!
辺と面積の関係を理解する
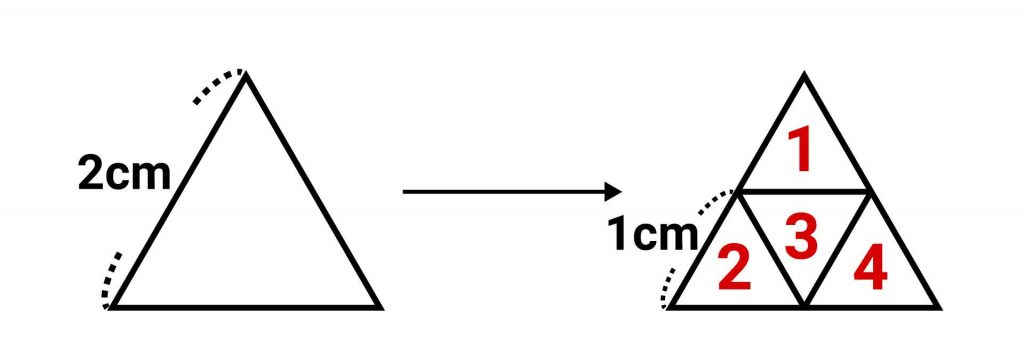
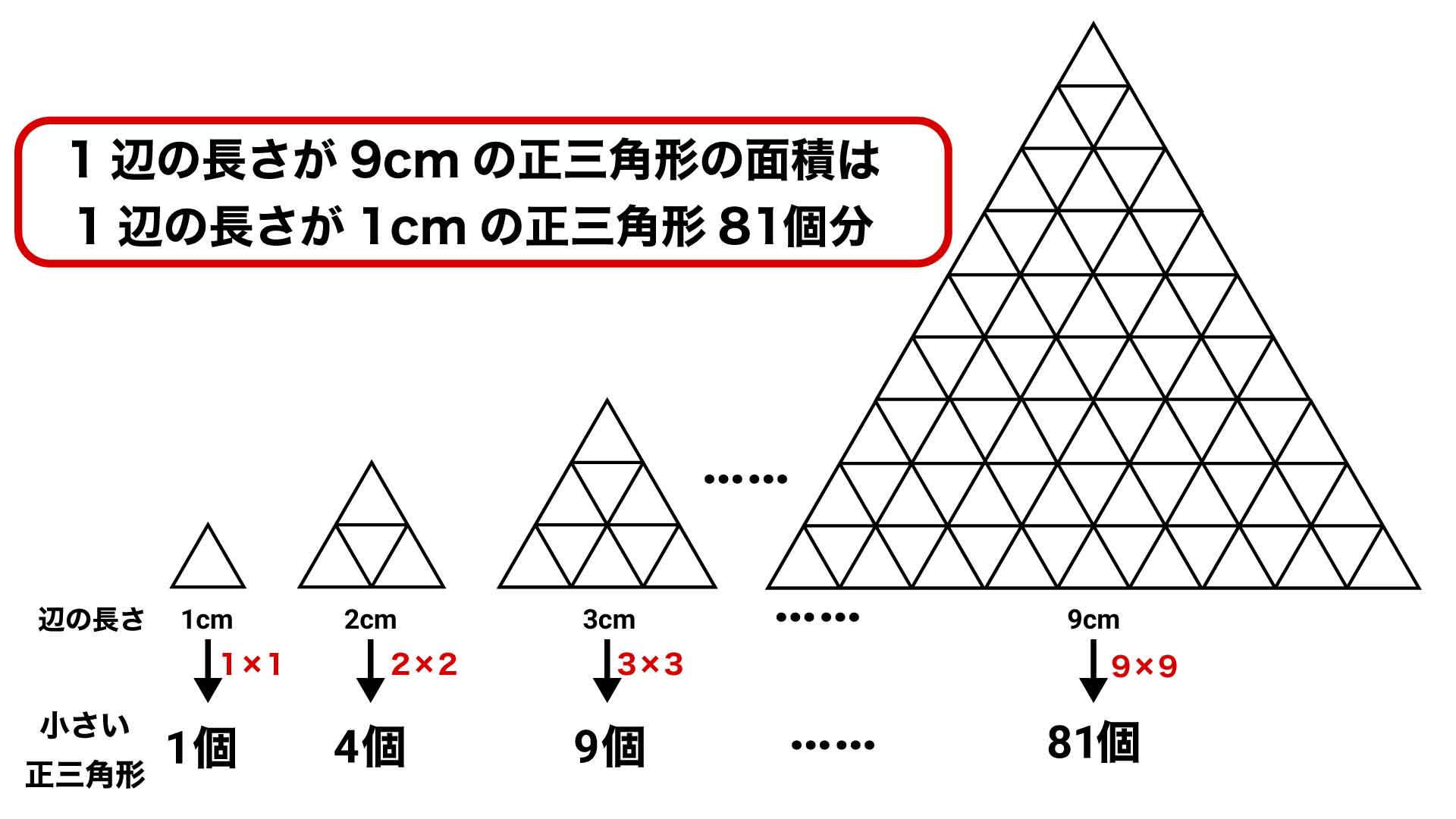
はじめに、一辺が2cmの正三角形に、一辺が1cmの正三角形(以降、この三角形を「小さな三角形」と呼びます)がいくつ入るかを考えてみます。
図のように分解すると、一辺が2cmの正三角形には、小さな三角形が4つ入ることがわかります。
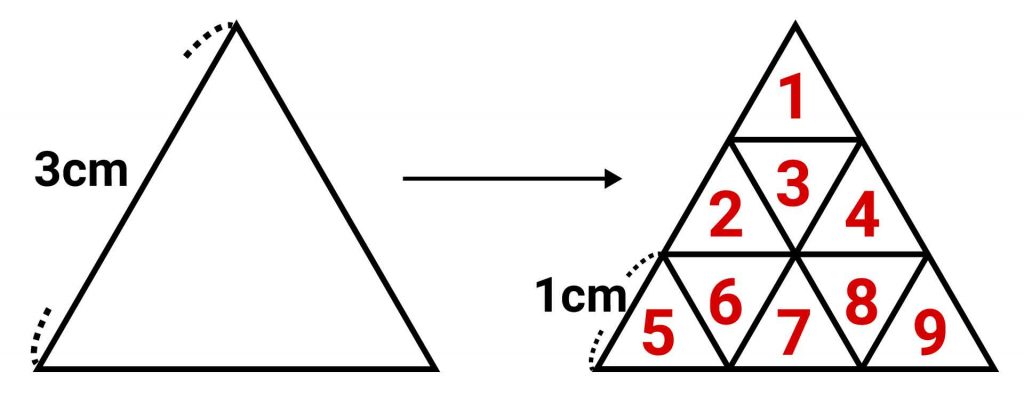
同じように、一辺が3cmの正三角形に小さな三角形がいくつ入るかを考えてみると、下の図のように小さな三角形が9つ入ることがわかります。
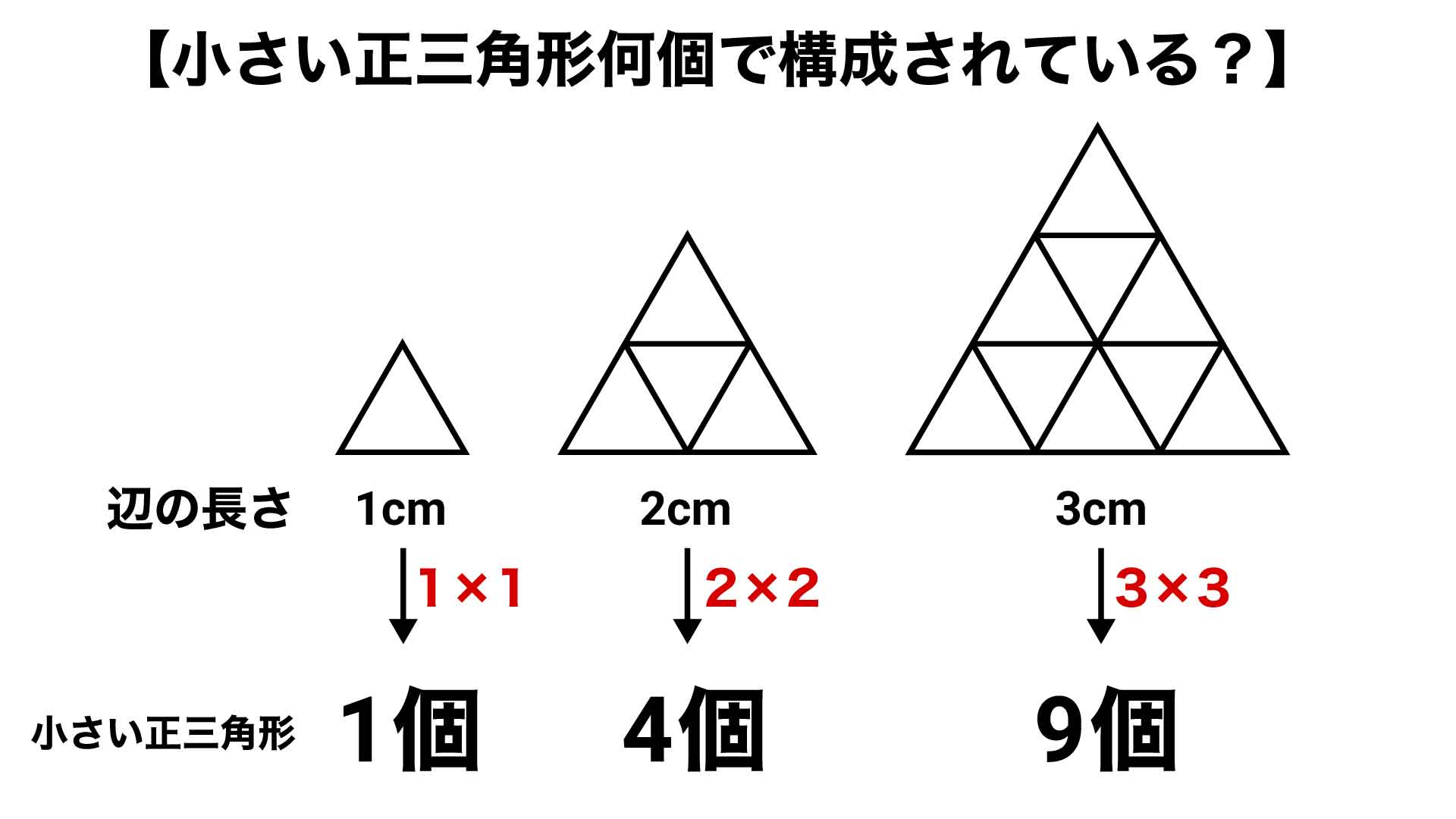
ここで、2と4、3と9という数字に着目すると、4は2×2、9は3×3と表すことができます。つまり、ある正三角形Aは、小さな正三角形が「(Aの1辺の長さ)×(Aの1辺の長さ)」個集まって構成されていることがわかります。
いろんな正三角形を作る
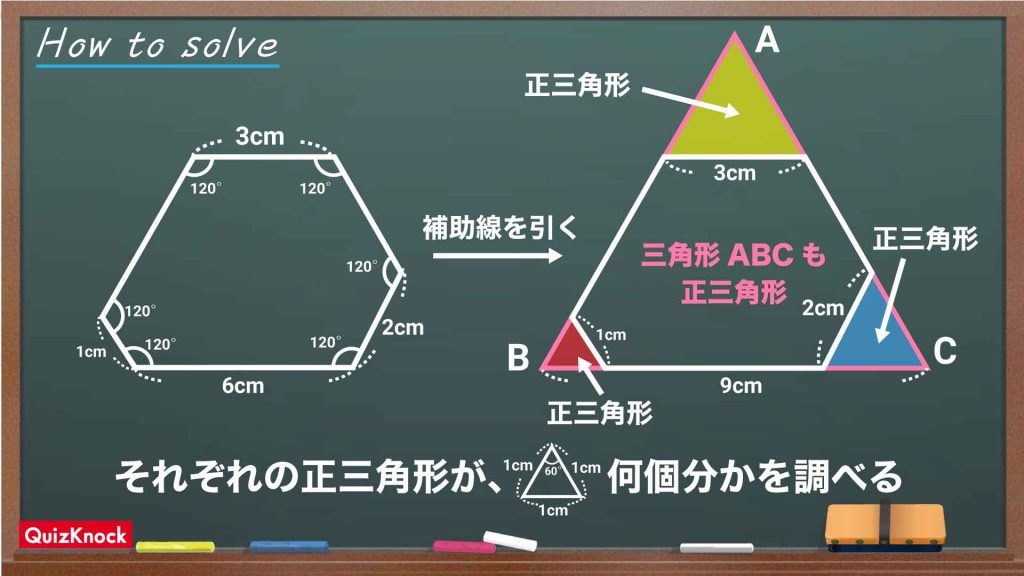
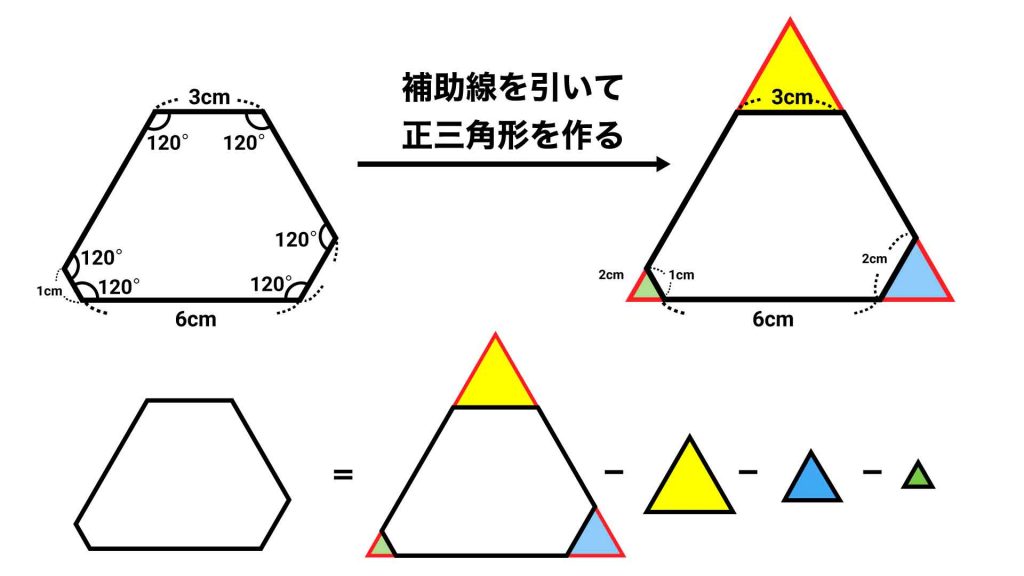
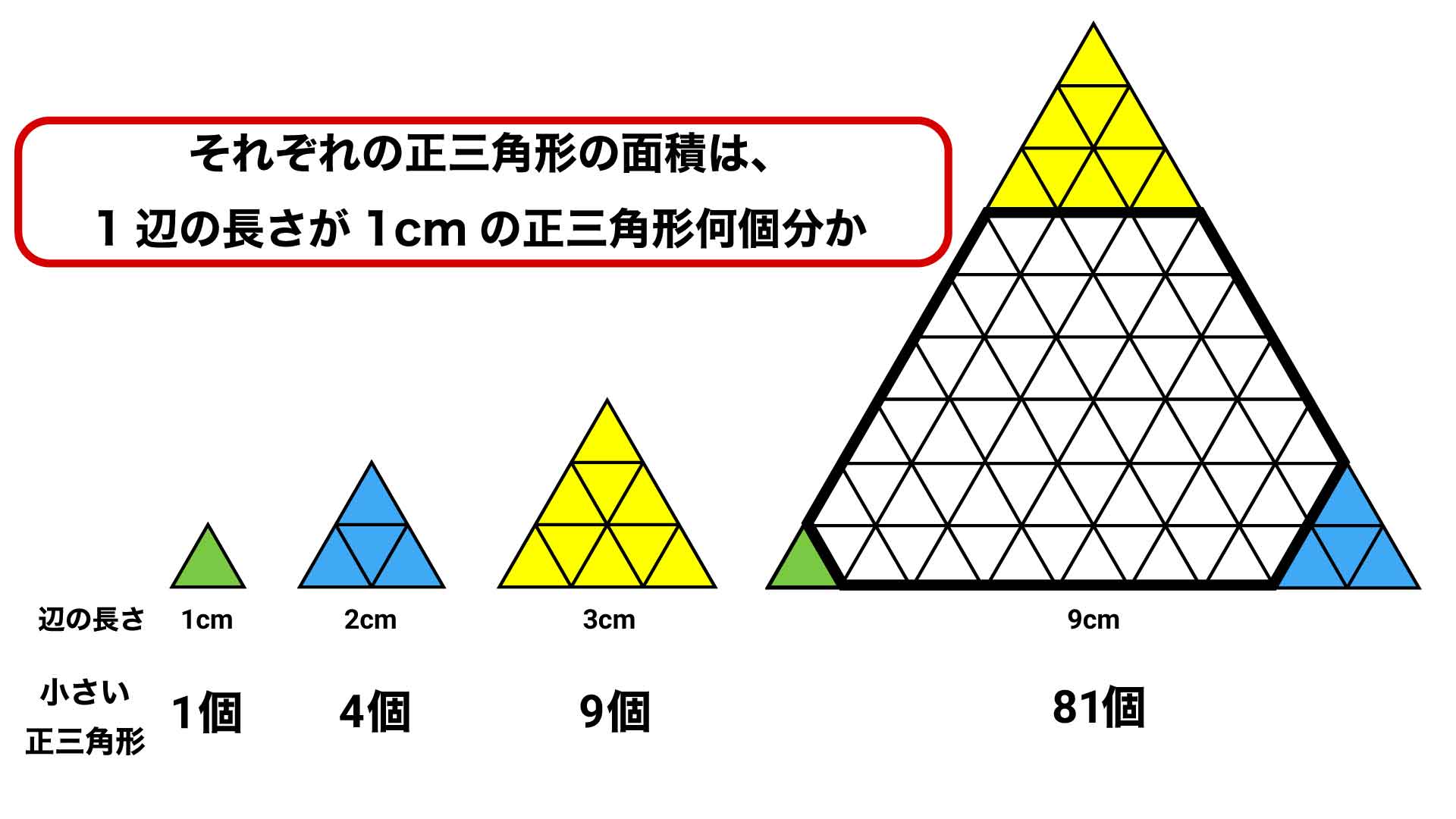
設問の六角形に、図のように補助線を引きます。すると、一つの大きな正三角形と、3つの正三角形ができます。したがって、六角形の面積は、大きな正三角形から3つの正三角形を引くことで求められます。
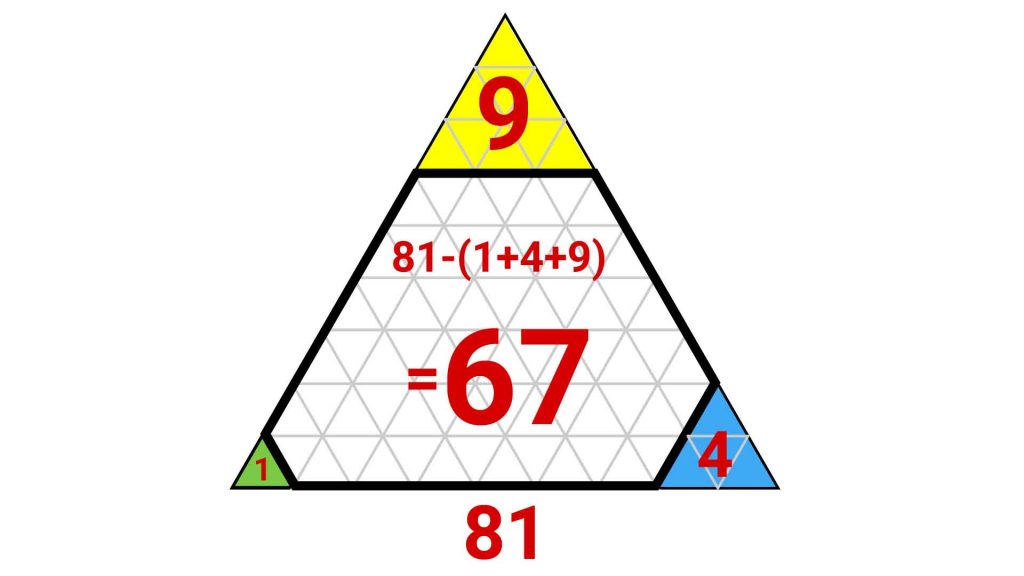
大きな正三角形の辺の長さは、1+6+2=9cmです。先ほど説明した辺の長さと面積の関係を用いると、大きな正三角形は9×9=81個の小さな三角形でできていることがわかります。
また、大きな正三角形の頂点にある3つの正三角形は、先ほど求めたように1つ、4つ、9つの小さな正三角形でできていることがわかります。
したがって、求める六角形は、81-(1+4+9)=67個の小さな三角形でできているため、答えは67倍となります。
答え:67倍
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)