解説
それでは解説です。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
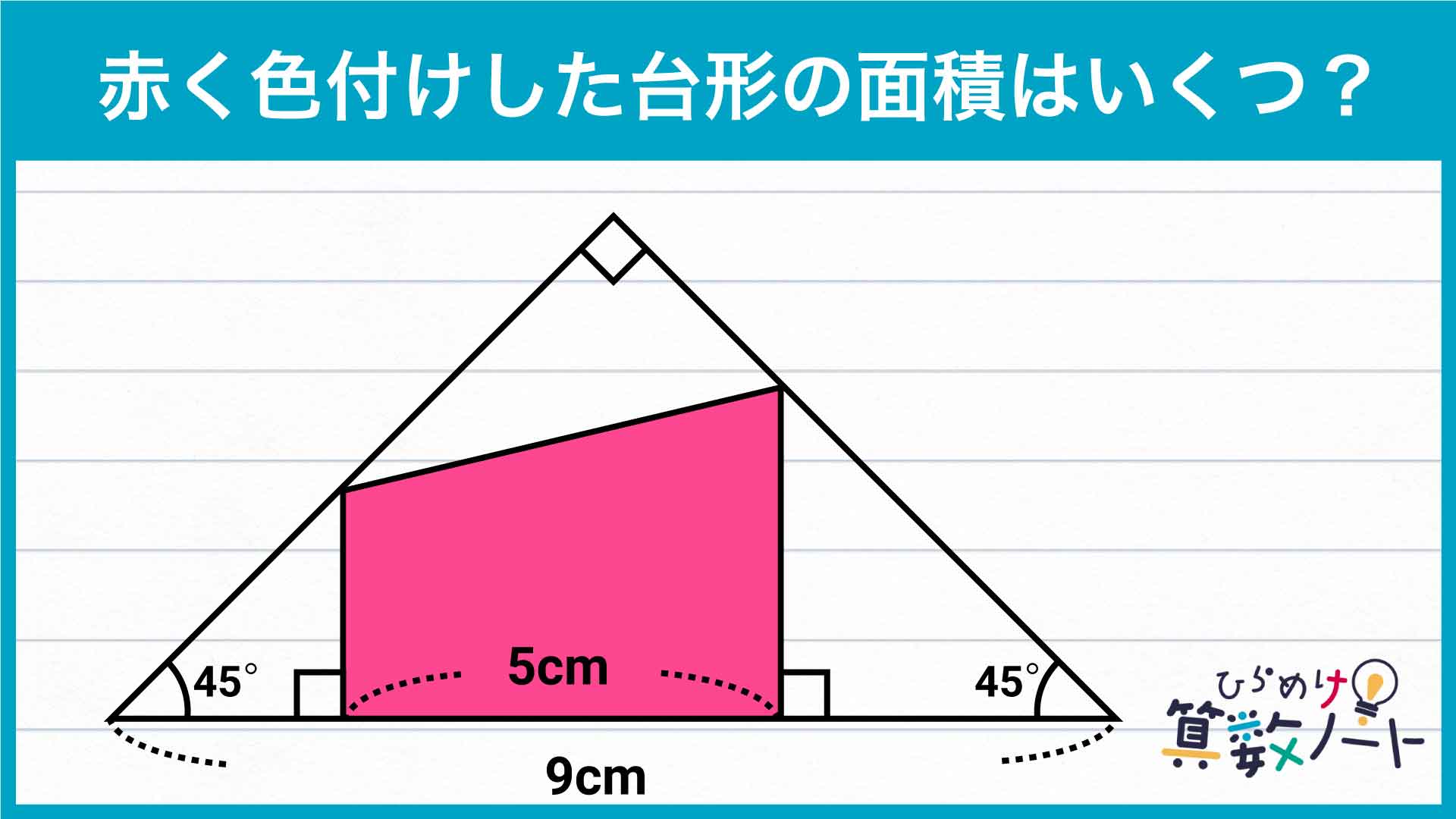
今回の問題の解き方をまとめた図がこちらです。ポイントは台形の面積の公式から考え、小さな直角二等辺三角形を見つけることです。
この図の流れに沿って、解いていきましょう!
同じ長さの辺を探そう!
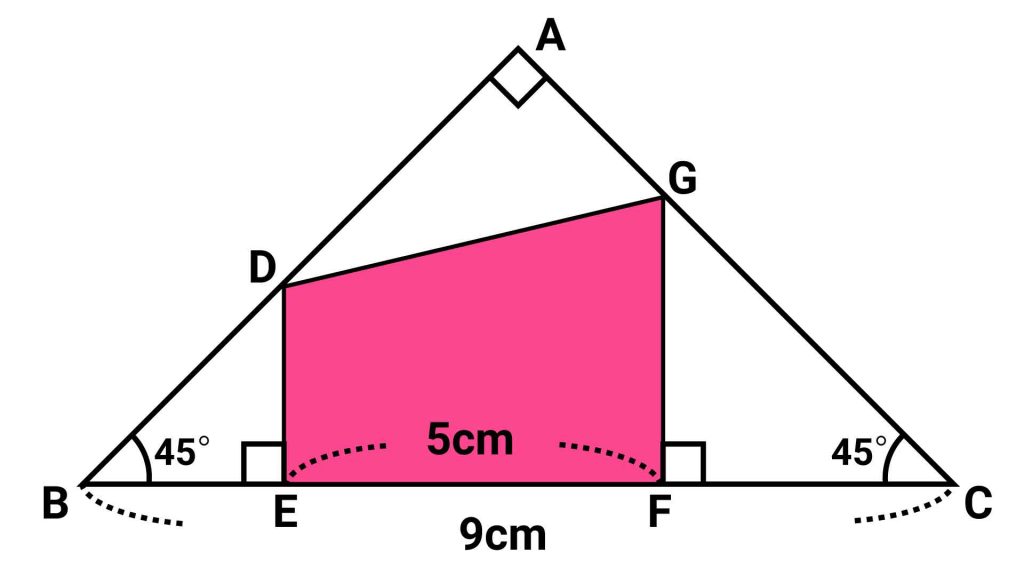
まずは、直角二等辺三角形と台形を組み合わせた図形から、同じ長さの辺を探してみましょう。
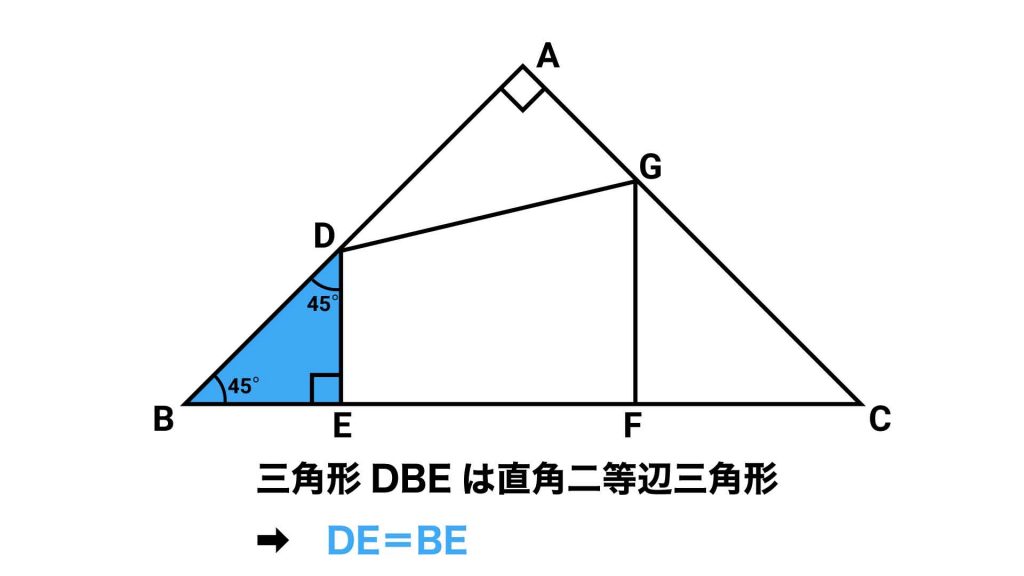
三角形DBEに着目すると、角DEBは直角で、三角形ABCが直角二等辺三角形であることから角DBEは45度であることがわかります。そして、三角形の内角の和は180度であることから、角BDEは、180-90-45=45度であり、三角形DBEは直角二等辺三角形となります。
したがって、BE=DEとなることがわかりました。
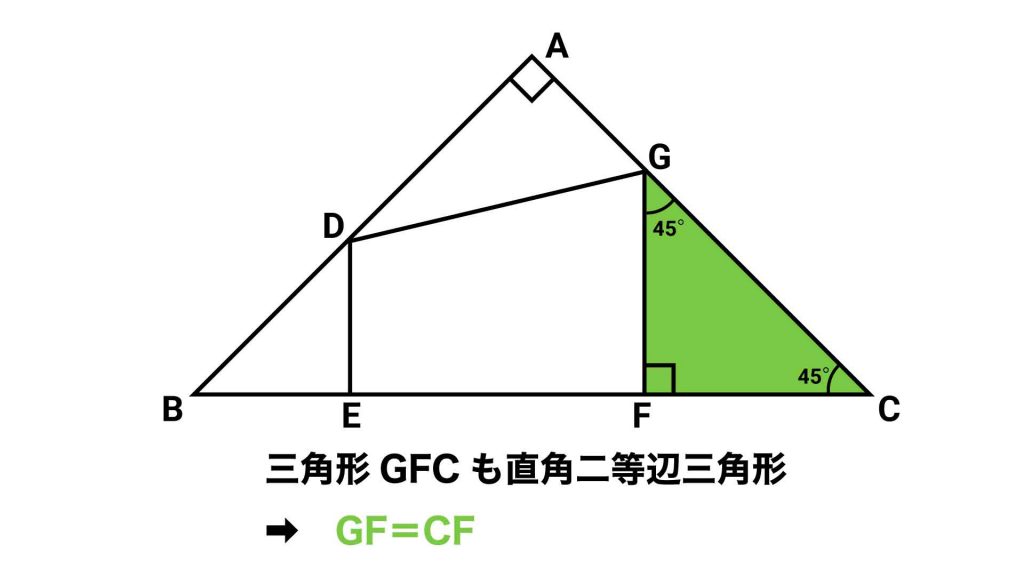
同様に、三角形GFCに着目すると、角CFGは直角で、三角形ABCが直角二等辺三角形であることから角FCGは45度であることがわかります。そして、三角形の内角の和は180度であることから、角CGFは、180-90-45=45度であり、三角形GFCは直角二等辺三角形となります。
三角形GFCが直角二等辺三角形であることから、CF=GFとなります。
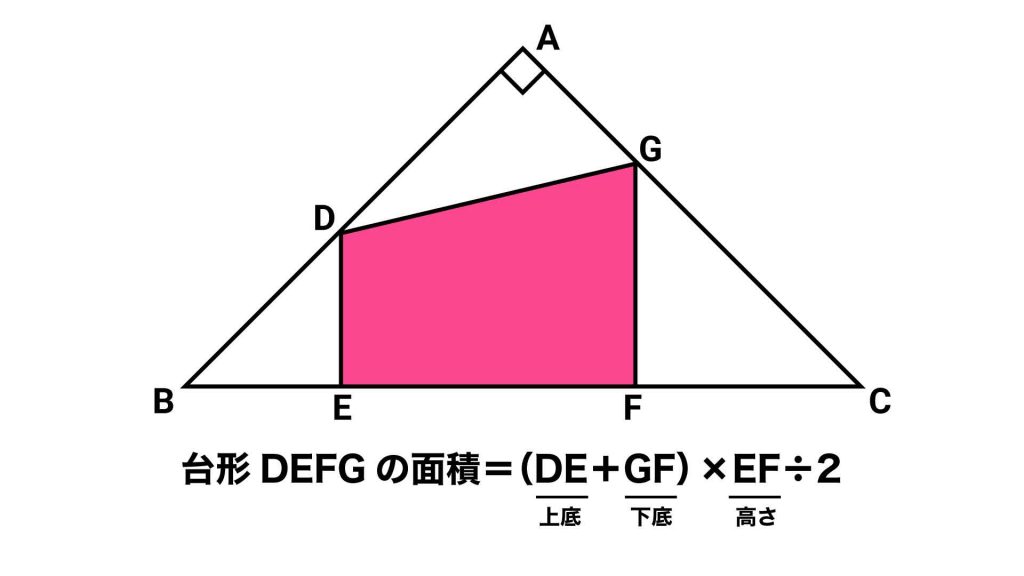
台形の面積の公式は?
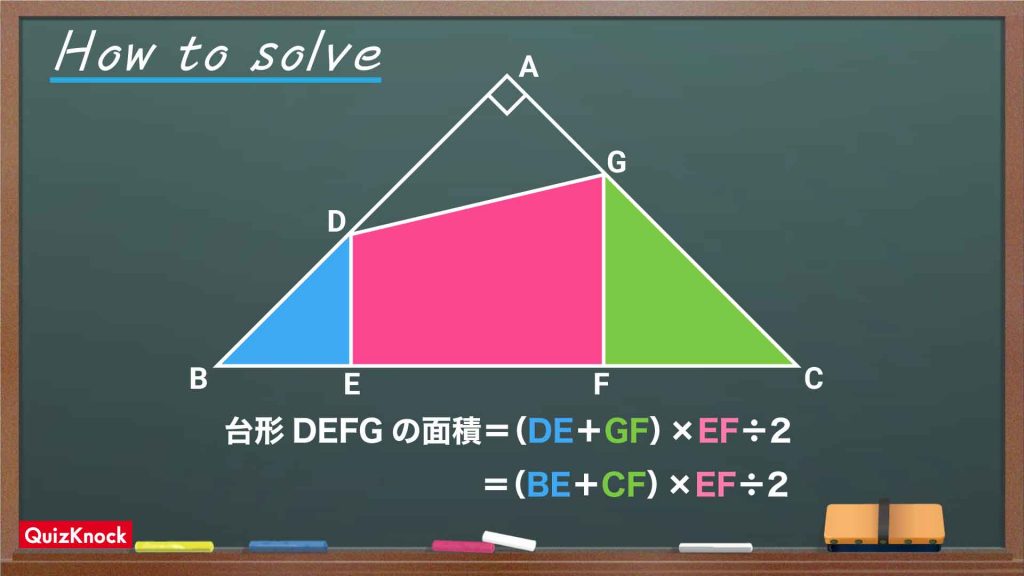
台形の面積は、(上底+下底)×高さ÷2という公式で求められます。
台形DEFGに台形の面積の公式を適用し、上底を辺DE、下底を辺GFとします。すると、高さは辺EFとなり、台形の面積は(DE+GF)×EF÷2で求められます。
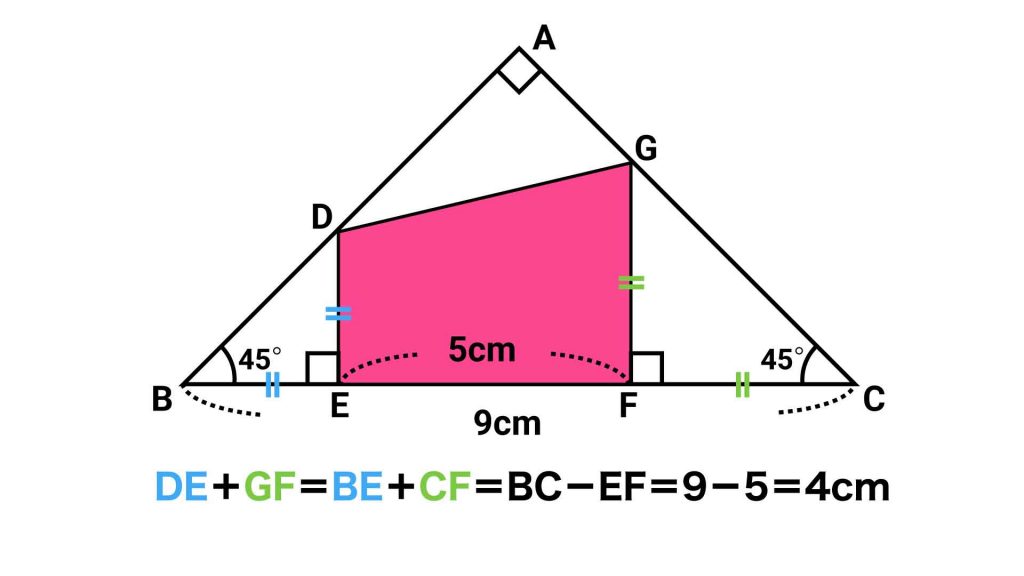
辺EFは5cmであることがわかっているので、辺DEと辺GFの長さの和がわかれば面積が求められます。
ここで、辺DEは辺BEと、辺GFは辺CFとそれぞれ長さが等しいことがわかっているため、DE+GF=BE+CFとなります。
BE+CFは、辺BCから辺EFを除いた部分の長さであるため、BE+CF=9-5=4cmとなります。
したがって、台形DEFGの面積は、4×5÷2=10cm2となります。
答え:10cm2
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)










.jpg)







