問題はこちら
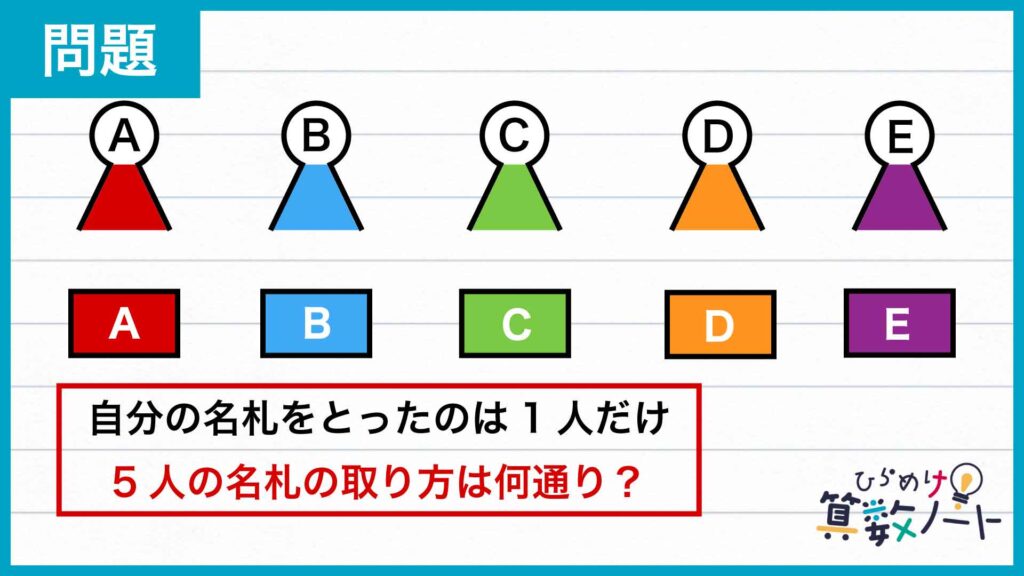
1ページ目:自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の問題を解くうえで重要なポイントを以下にまとめました。
整理すると、
- 「自分の名札を取った生徒」が誰かで場合分けする
- それぞれの場合で名札の取り方の数を求める
の2点です。これらのポイントを踏まえながら、問題を解いていきましょう。
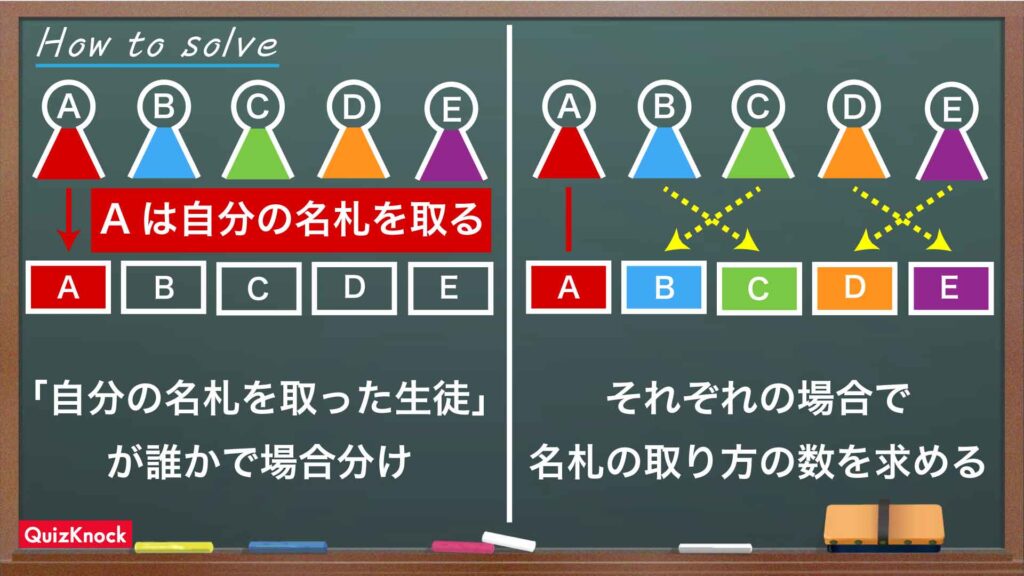
「自分の名札を取った生徒」が誰かで場合分けする
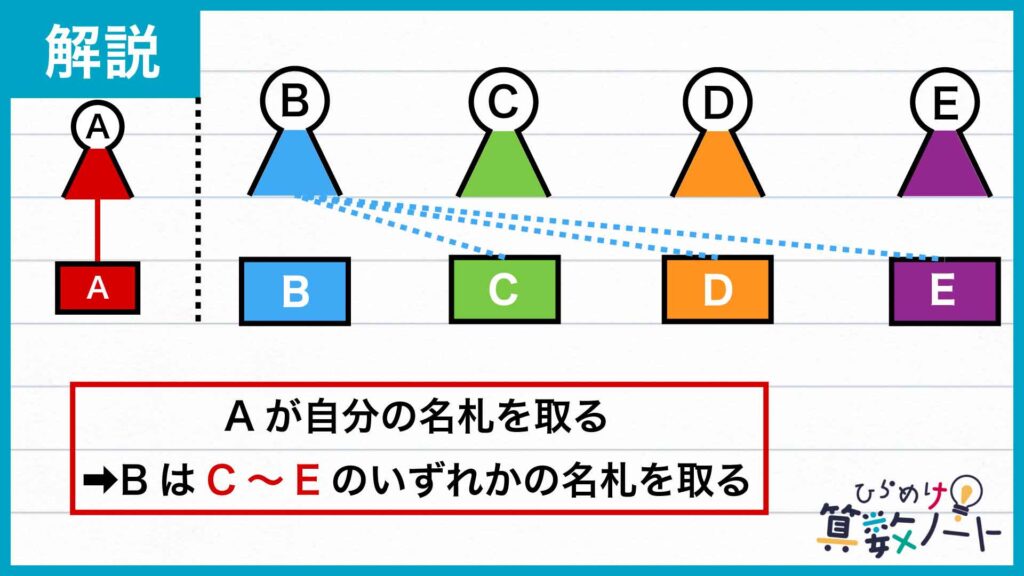
まず、1人だけいる「自分の名札を取った生徒」が誰かで場合分けをしてしましょう。ここでは、自分の名札を取った生徒がAである場合を考えます。
すると、問題の条件から、残り4人の生徒は全員自分とは別の人の名札を取っていることがわかります。
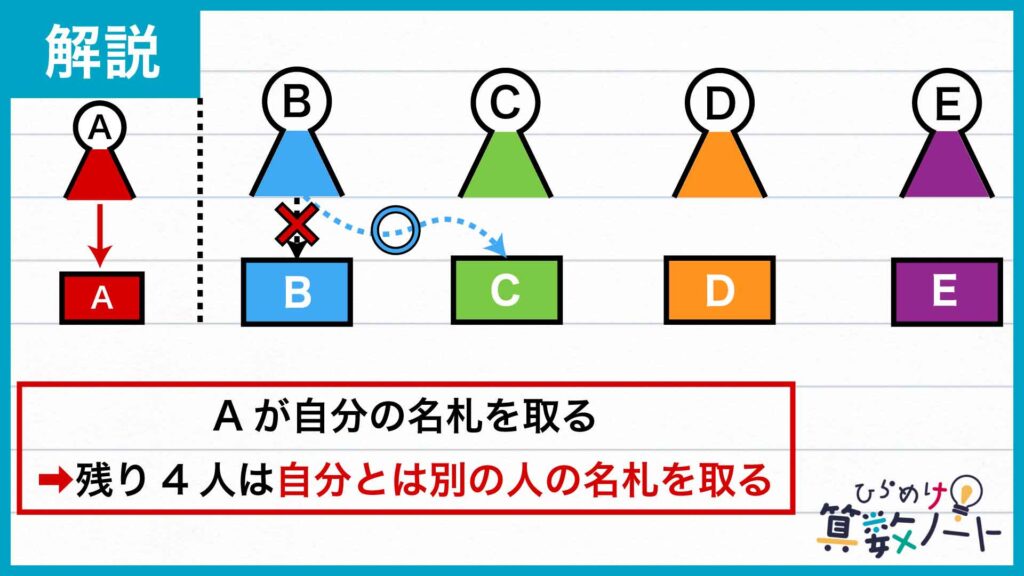
それぞれの場合で名札の取り方の数を求める
では、自分の名札を取った生徒がAであるときの、残りの生徒の名札の取り方の総数を求めましょう。まず、生徒Bは問題の条件から自分のものではない名札を取っているので、C、D、Eのどれかの名札を取っています。
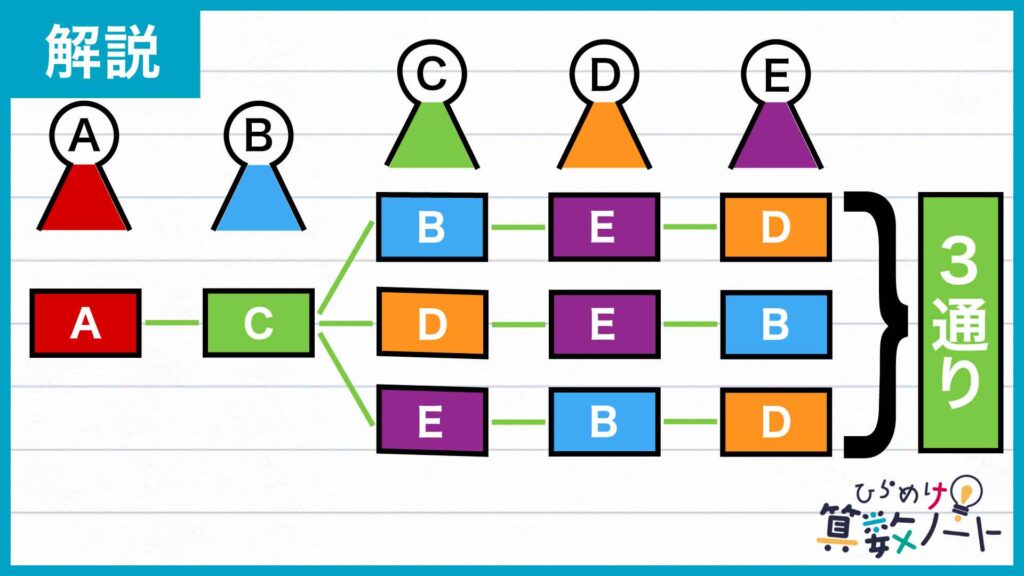
生徒BがCの名札を取った場合、残っているのはB、D、Eの名札です。これらの名札を生徒C、D、Eの3人が取る場合の数は、下の図のように3通りであることがわかります。
生徒Bが、DまたはEの名札を取った場合も同様に考えることができます。下の図から、それぞれの場合の数は同じ3通りです。
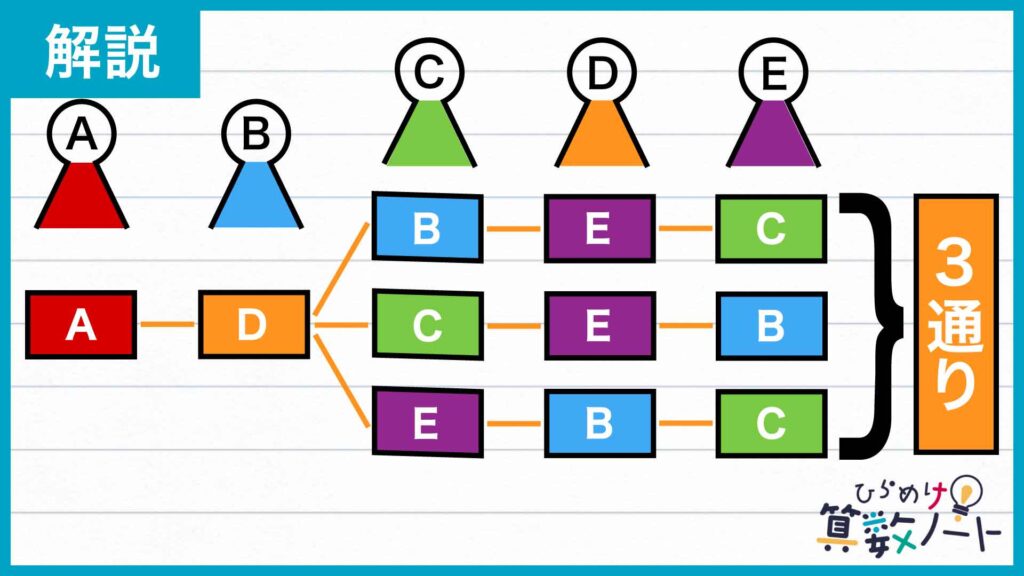
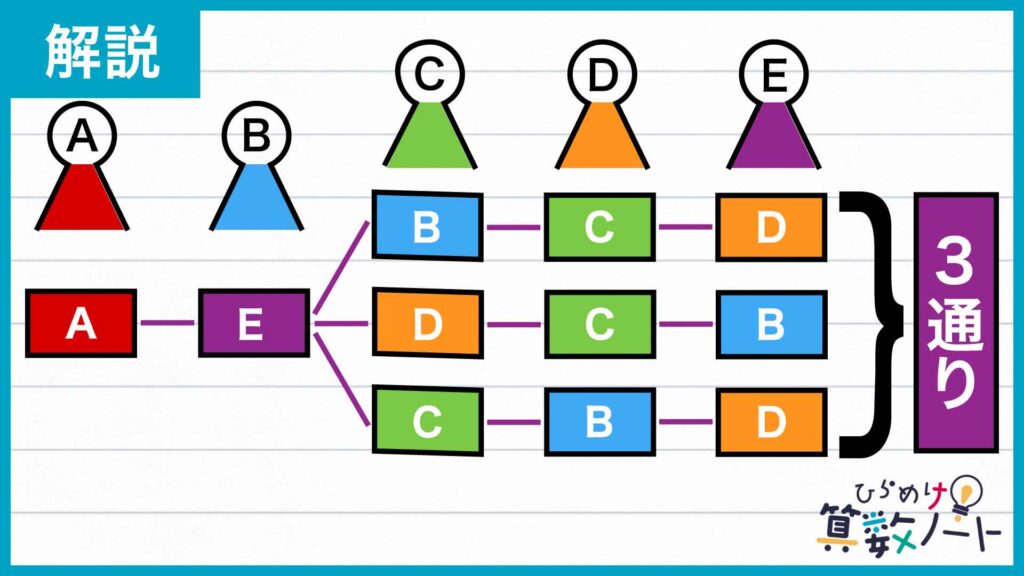
したがって、自分の名札を取った生徒がAであるときの、残りの生徒の名札の取り方の総数は3通り×3=9通りです。
自分の名札を取った生徒がB~Eのいずれかである場合も全く同じ方法で考えることができて、残りの生徒の名札の取り方も同じく9通りになります。
よって、求める場合の数は9通り×5=45通りとなります。
答え:45通り
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】











.jpg)








.jpg)







