小学生で解ける「図形の面積」を求める問題、あなたは解けますか？

ヒント

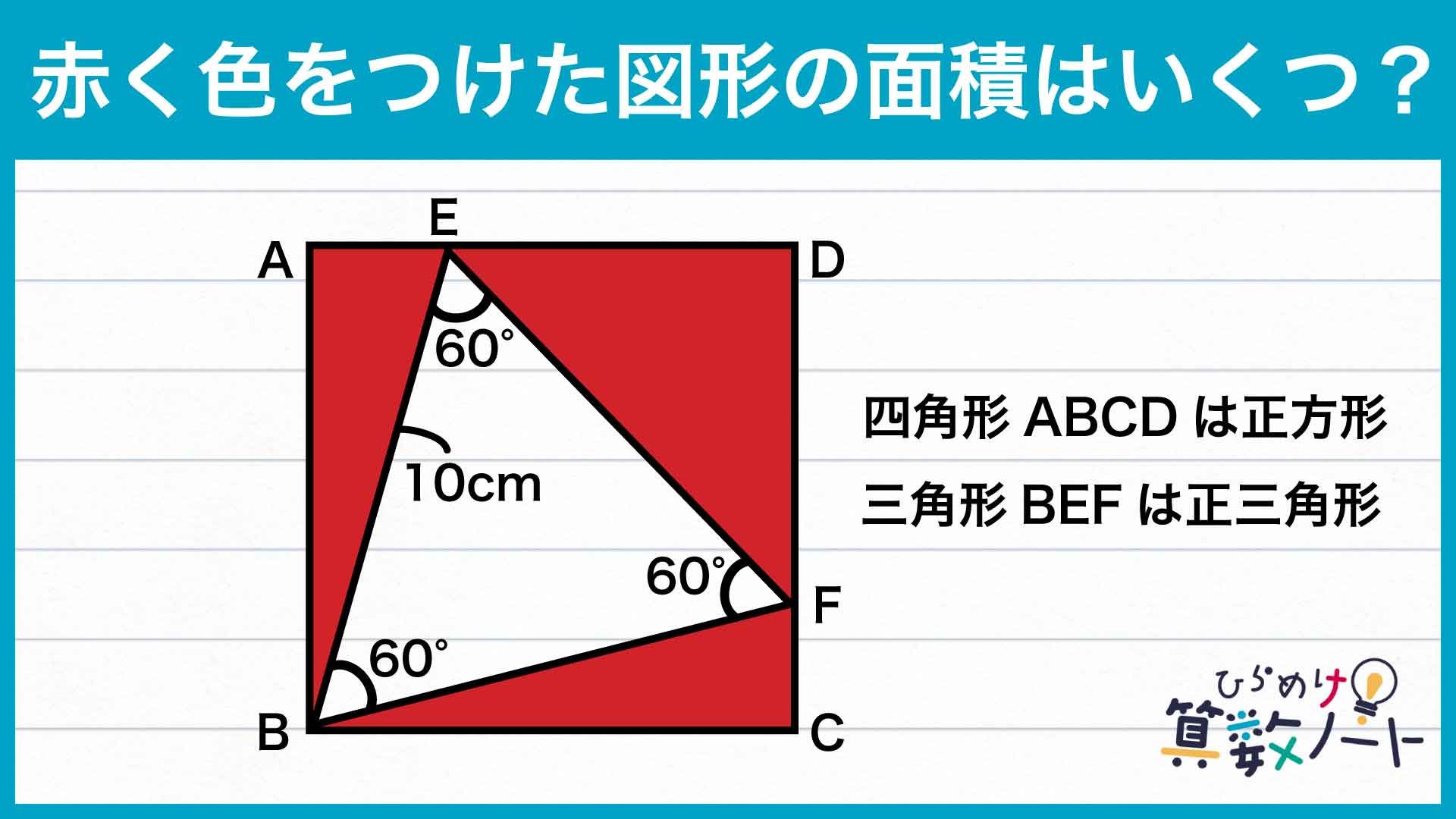
面積を求める図形を、下のように青色の部分と緑色の部分の2つの部分に分けて考えましょう。

このうち、青色の部分の2つの三角形ABEと三角形CBFに注目します。まず三角形BEFは正三角形なので、BE=BFです。また、四角形ABCDは正方形であるので、AB=CBであり、角BAE=角BCF=90度が成り立ちます。

したがって、「直角三角形の斜辺と他の一辺の長さが等しい」ことから、三角形ABEと三角形CBFは合同な直角三角形になります。

3ページ目：【答え＆解説】どのように面積を求めるのがよいでしょうか？　答えがわからない場合はこちらへ