小学生で解ける「図形の面積」を求める問題、あなたは解けますか？

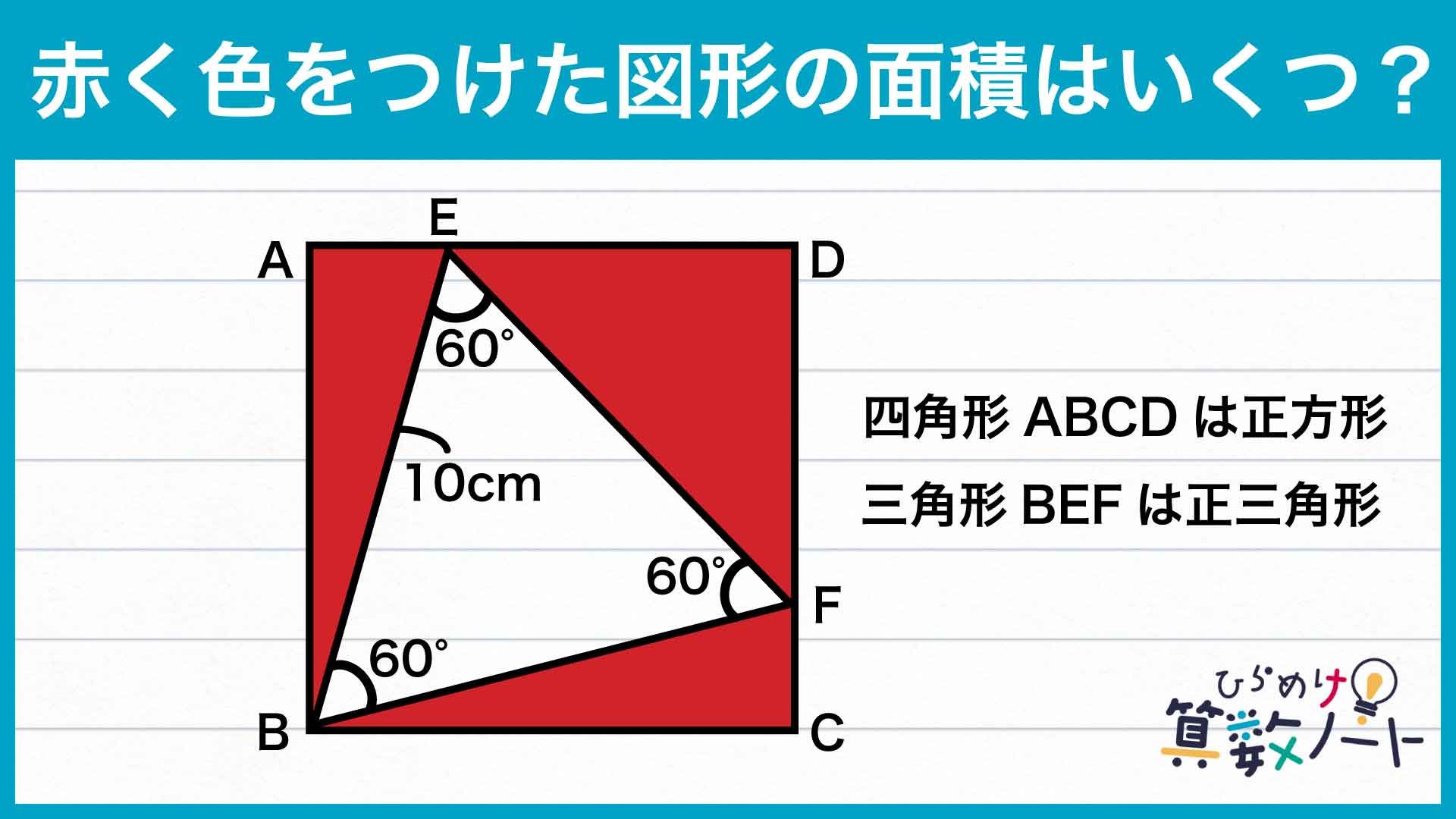
問題はこちら

1ページ目：自力で解きたい方はこちらへ！　以下は問題の解説です

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

今回の問題を解くうえで重要なポイントを以下にまとめました。

整理すると、

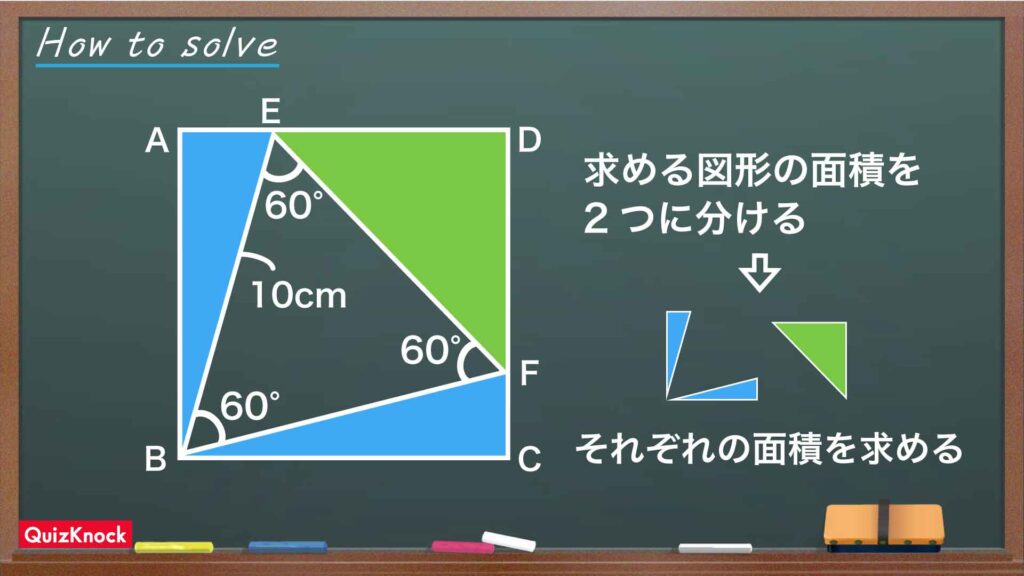
• 面積を求める図形を2つに分ける
• 青い部分の面積を求める
• 緑の部分の面積を求める

の3点です。これらのポイントを踏まえながら、問題を解いていきましょう。

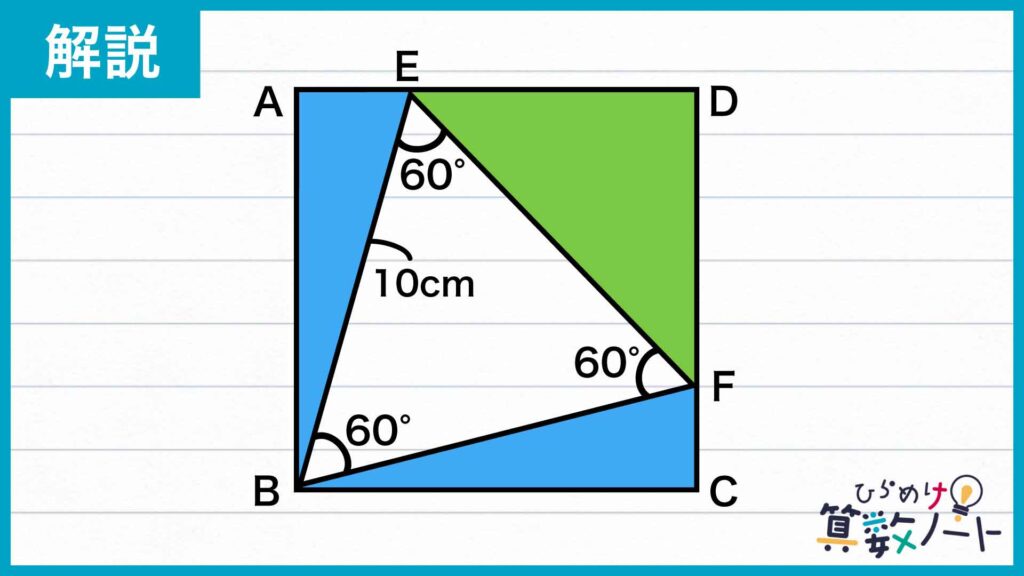
面積を求める図形を2つに分ける

面積を求める図形を、下のように青色の部分と緑色の部分の2つの部分に分けて考えましょう。

青色の部分の面積を求める

上の図で分けた2つの部分のうち、まずは青色の部分の面積を求めます。
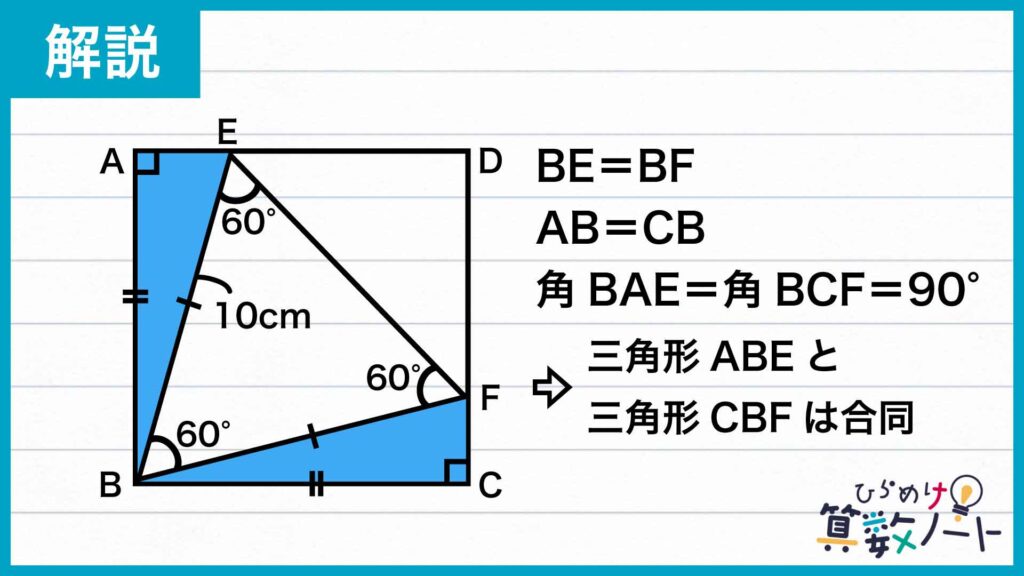
まず、2つの三角形ABEと三角形CBFに注目します。まず三角形BEFは正三角形なので、BE=BFです。また、四角形ABCDは正方形であるので、AB=CBであり、角BAE=角BCF=90度が成り立ちます。

したがって、「直角三角形の斜辺と他の一辺の長さが等しい」ことから、三角形ABEと三角形CBFは合同な直角三角形になります。

よって、角ABE=角CBFです。また、角ABE+角CBF＋角EBF=角ABC=90度であり、正三角形の1つの角である角EBFの大きさは60度であるので、角ABE+角CBF=30度であることがわかります。したがって、角ABE=角CBF=15度となります。

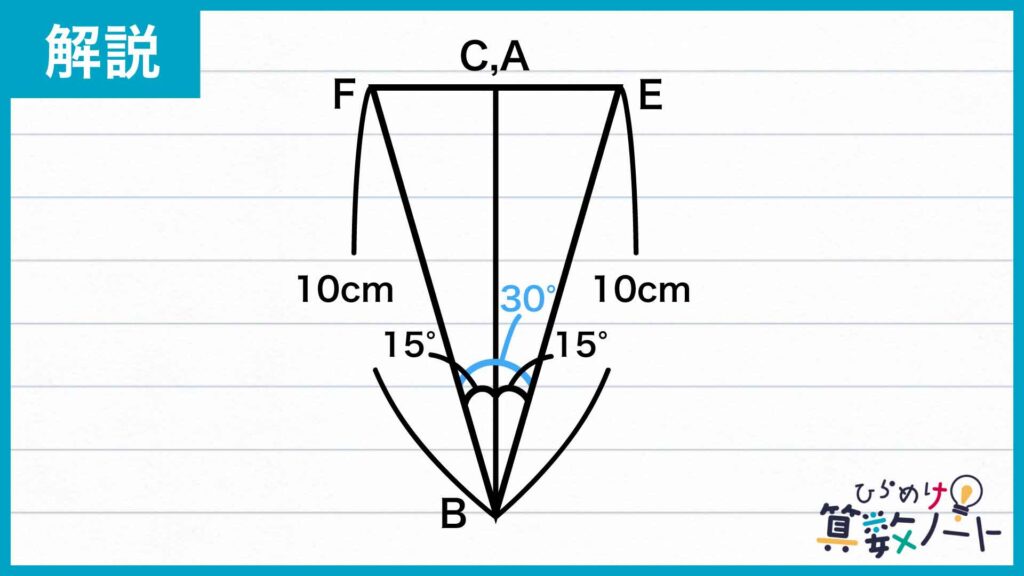
ここで、AB=CBであることから、三角形ABEと三角形CBFを辺ABと辺CBでぴったり合わせてみましょう。このとき、角BAE=角BCF=90度より、角BAE+角BCF=180度であるので、点B、点A、点Fは一直線上に並びます。

したがって、三角形ABEと三角形CBFを合わせると、下の図のような大きな三角形BEFができます。このうち、角EBFの大きさは、角EBF=角EBA+角FBC=30度です。

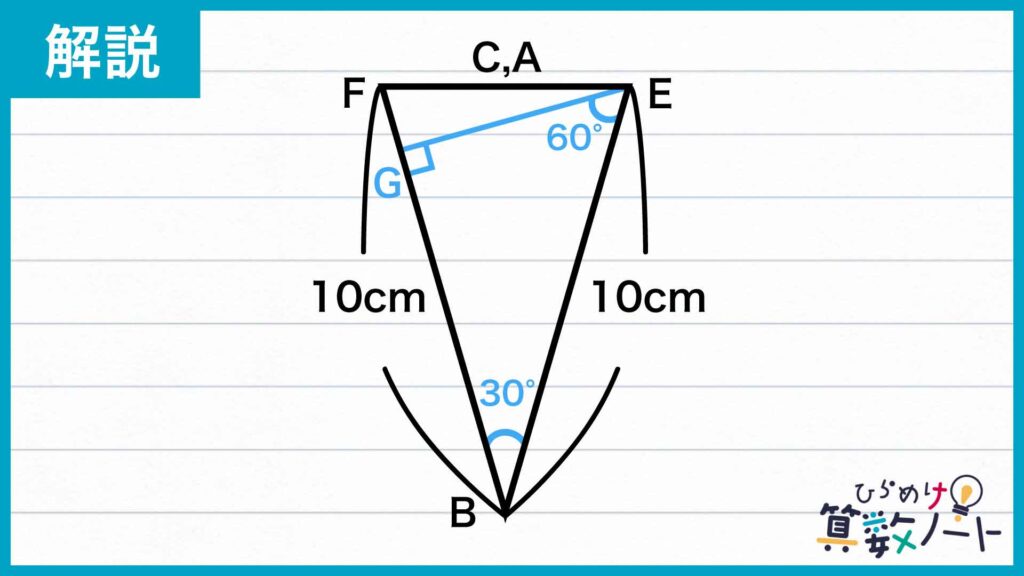
ここで、下の図のように点Eから辺BFに垂直に線を下ろし、辺BFとの交点をGとします。

三角形EGBのみに注目し、三角形EGBを辺BGについて折り返した三角形HGBを、元の三角形EGBに合わせます。このとき、角EGB=角HGB=90度より、角EGB+角HGB=180度であるので、点E、点G、点Hは一直線上に並びます。

したがって、三角形EGBと三角形HGBを合わせると、下の図のような大きな三角形BEHができます。ここで、角BEH=角BHE=角EBH=60度より、三角形BEHは正三角形になります。

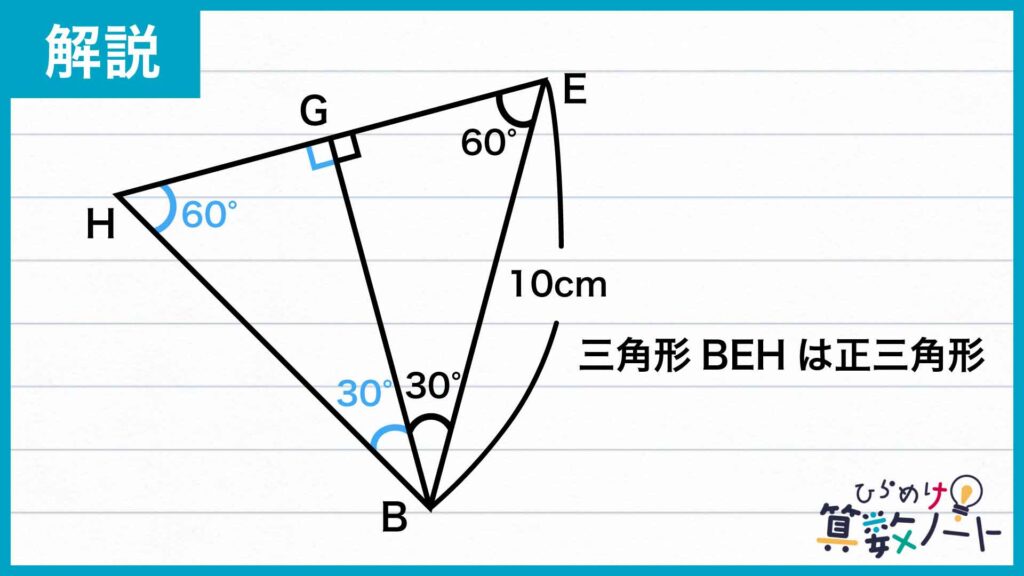
したがって、EH=BE=10cmなので、EHの長さは10cmです。さらに、三角形EGBと三角形HGBは合同なので、EG=HGより、EG=HG=5cmとなります。

以上のことから、三角形BFEの面積は、BF×EG÷2=10×5÷2=25cm²となります。したがって、元の青色の部分の面積は25cm²です。

緑色の部分の面積を求める

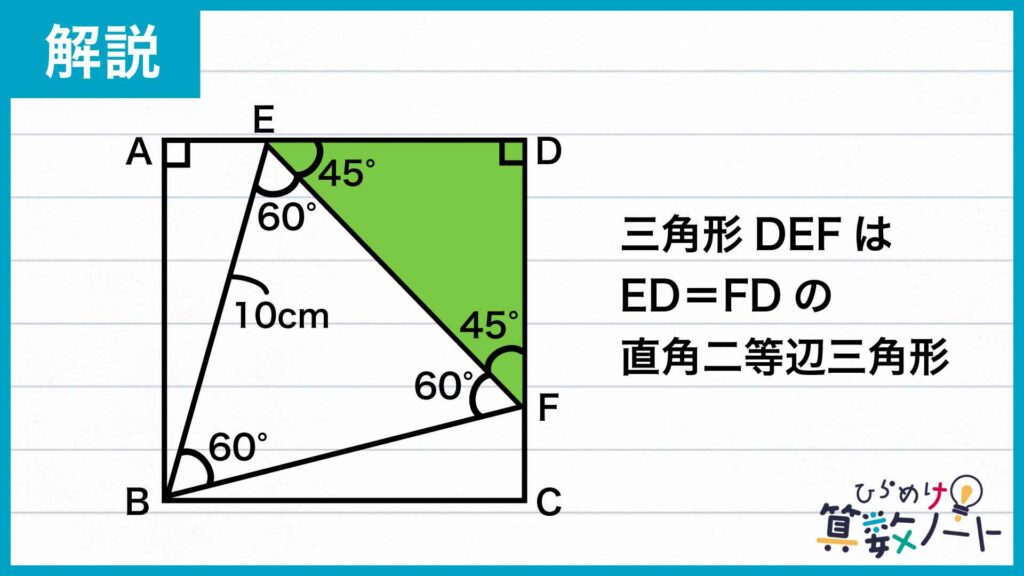
緑色の部分の三角形DEFに注目します。下の図のように、角EFD=180-角BFE-角BFC=180-60-75=45度です。同様にして、角FED=45度です。したがって、角EDF=90度もあわせて、三角形DEFはED=FDの直角二等辺三角形であることがわかります。

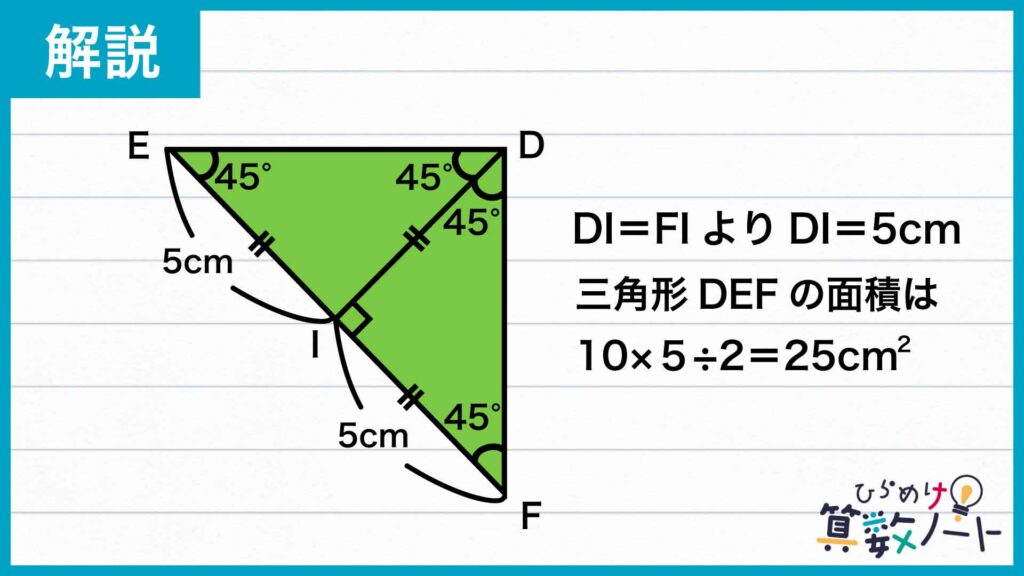
したがって、点DからEFに垂直に線を下ろし、EFとの交点をIとすると、二等辺三角形の性質から、EI=FIであることがわかります。EF=10cmなので、EI=FI=5cmです。

また、二等辺三角形の性質により、DIは角EDFを二等分するので、角EFD=45度です。角DFI=45度、角DIF=90度もあわせて、三角形DIFは直角二等辺三角形であることがわかります。したがって、DI=FI=5cmであるので、三角形DEFの面積は、EF×DI÷2=10×5÷2=25cmとなります。

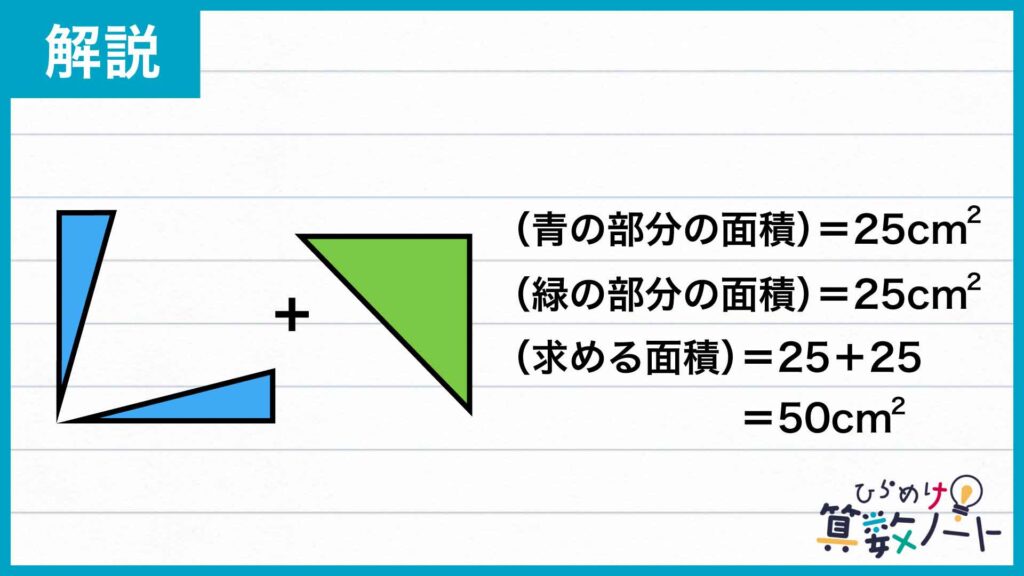
したがって、求める図形の面積は、（青色の部分の面積）+（緑色の部分の面積）=25+25=50cm²です。

答え：50cm²

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】