小学5年生で解ける「立体の表面積」を求める問題にチャレンジ！

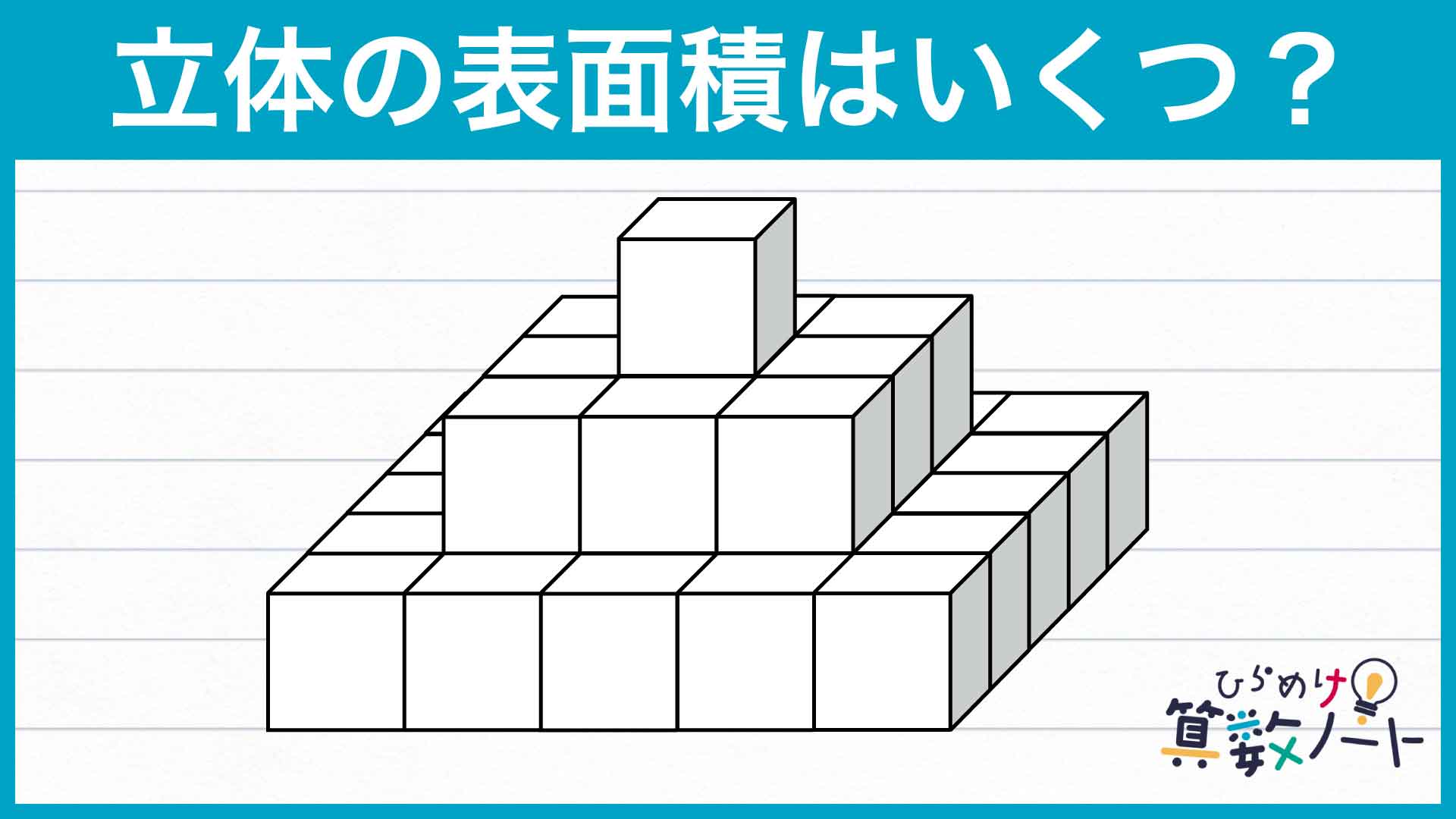
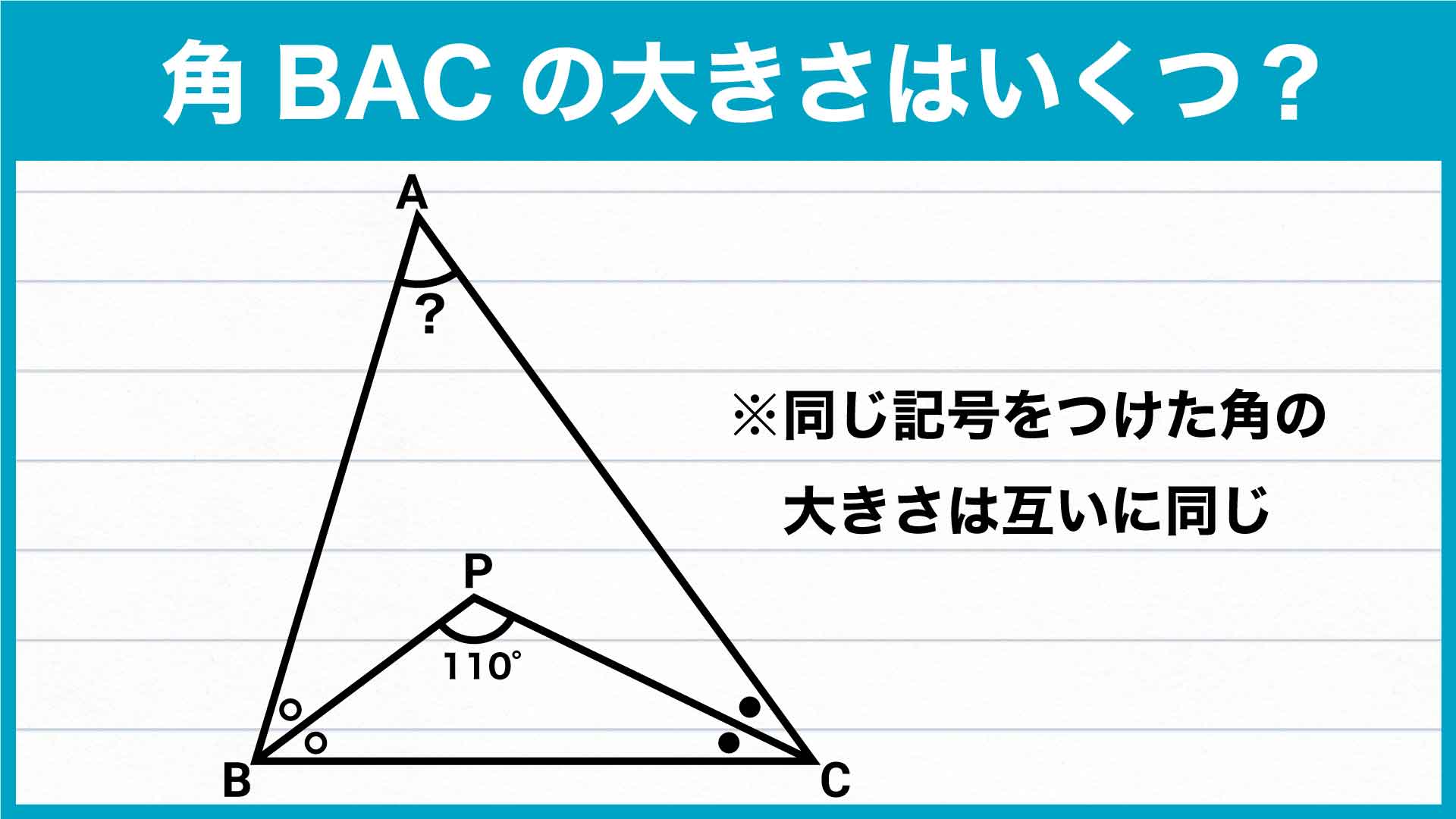
【問題はこちら】

1ページ目：自力で解きたい方はこちらへ！　以下は問題の解説です

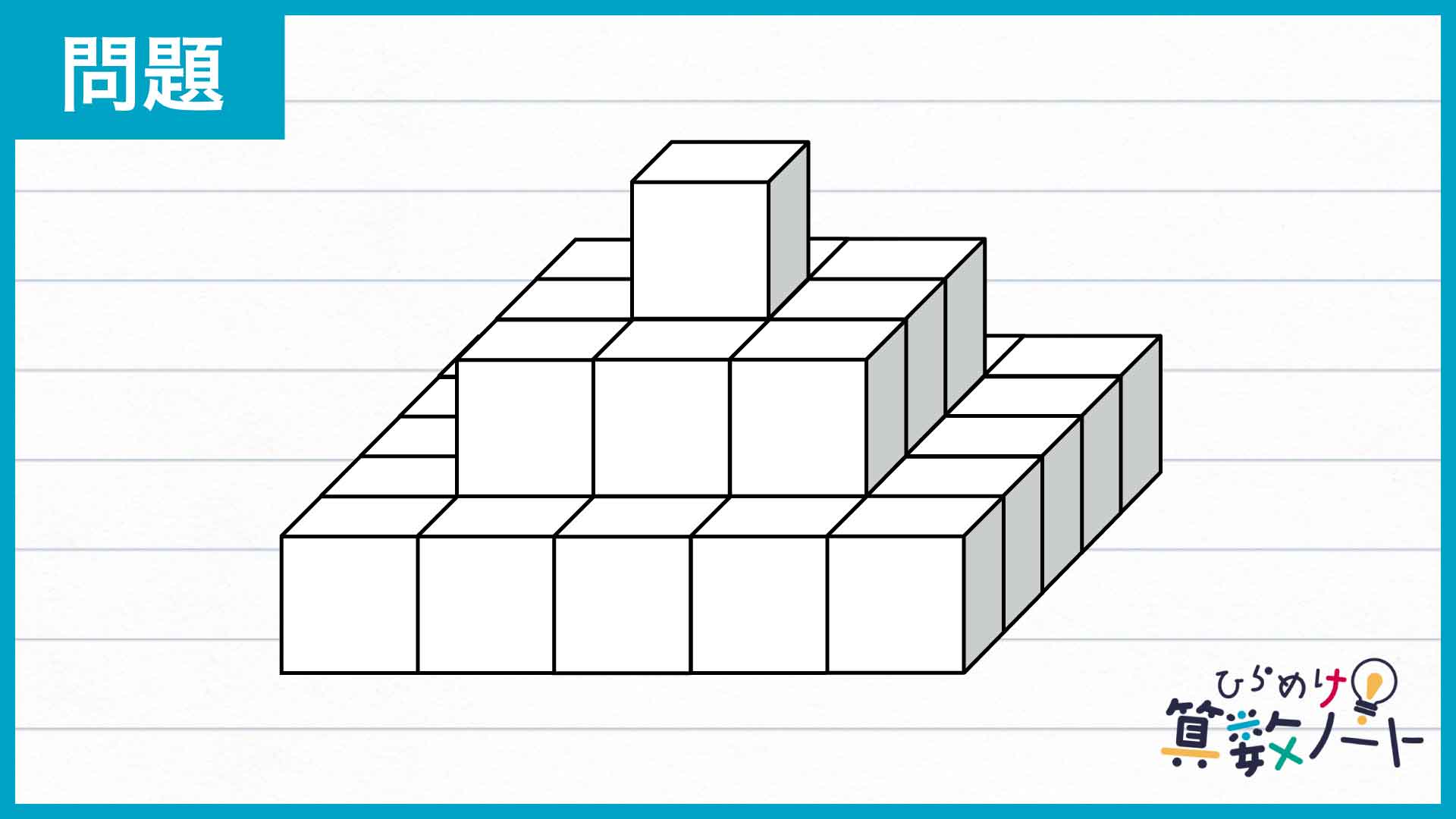
解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

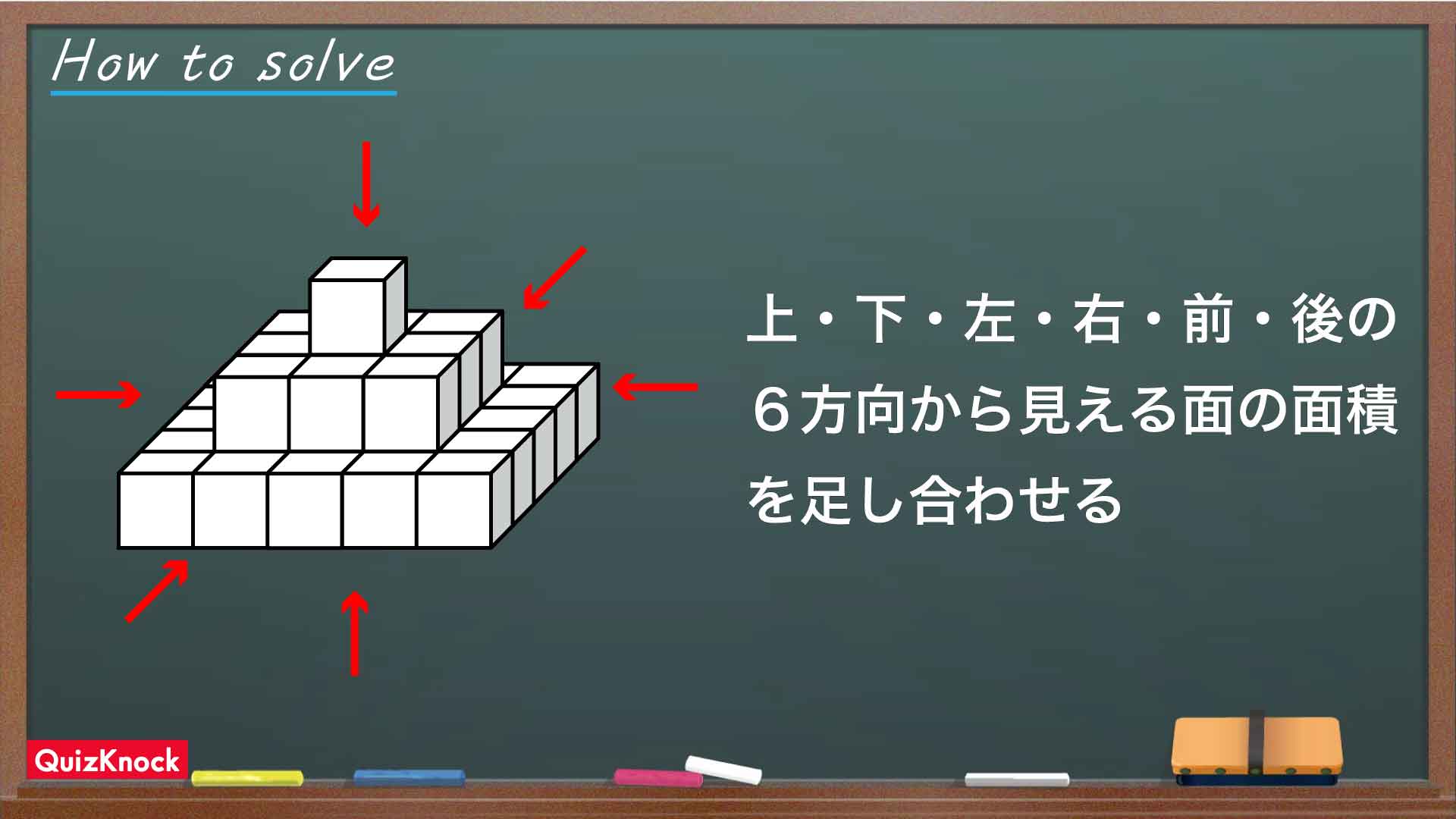
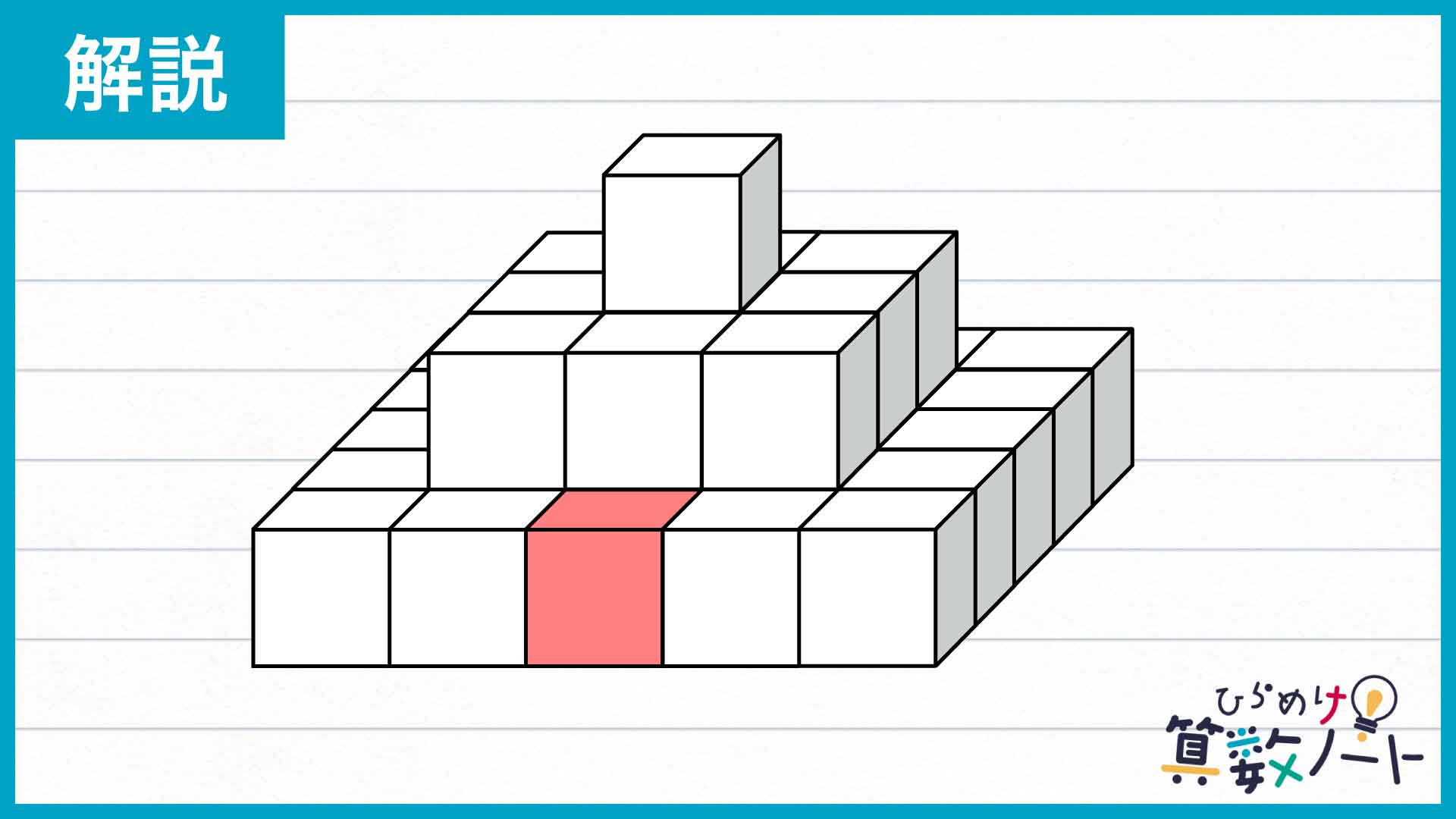
今回の問題の解き方をまとめた図がこちらです。

ポイントは、前・後・左・右・上・下の6方向から見える立体の面の面積を合計することです。これを踏まえて解いていきましょう！

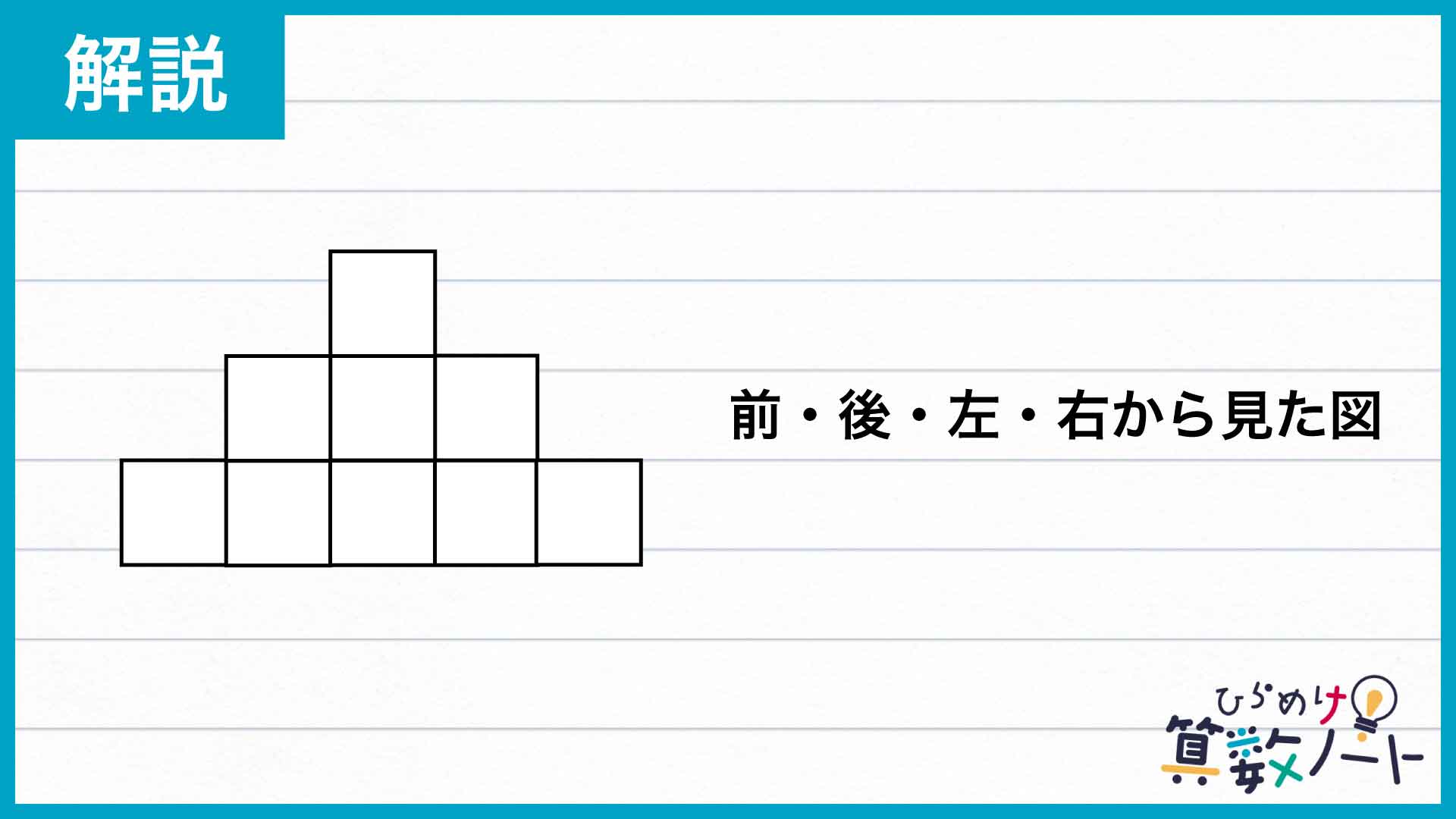
前・後・左・右から立体を見る

立体を前・後・左・右の4方向から見ると、いずれも次の図のように見えます。

立体にへこみが無いため、この図形の面積とそれぞれの方向の立体の表面積は同じです。よって、前・後・左・右の4方向の表面積は、(1+3+5)×4=36cm²となります。

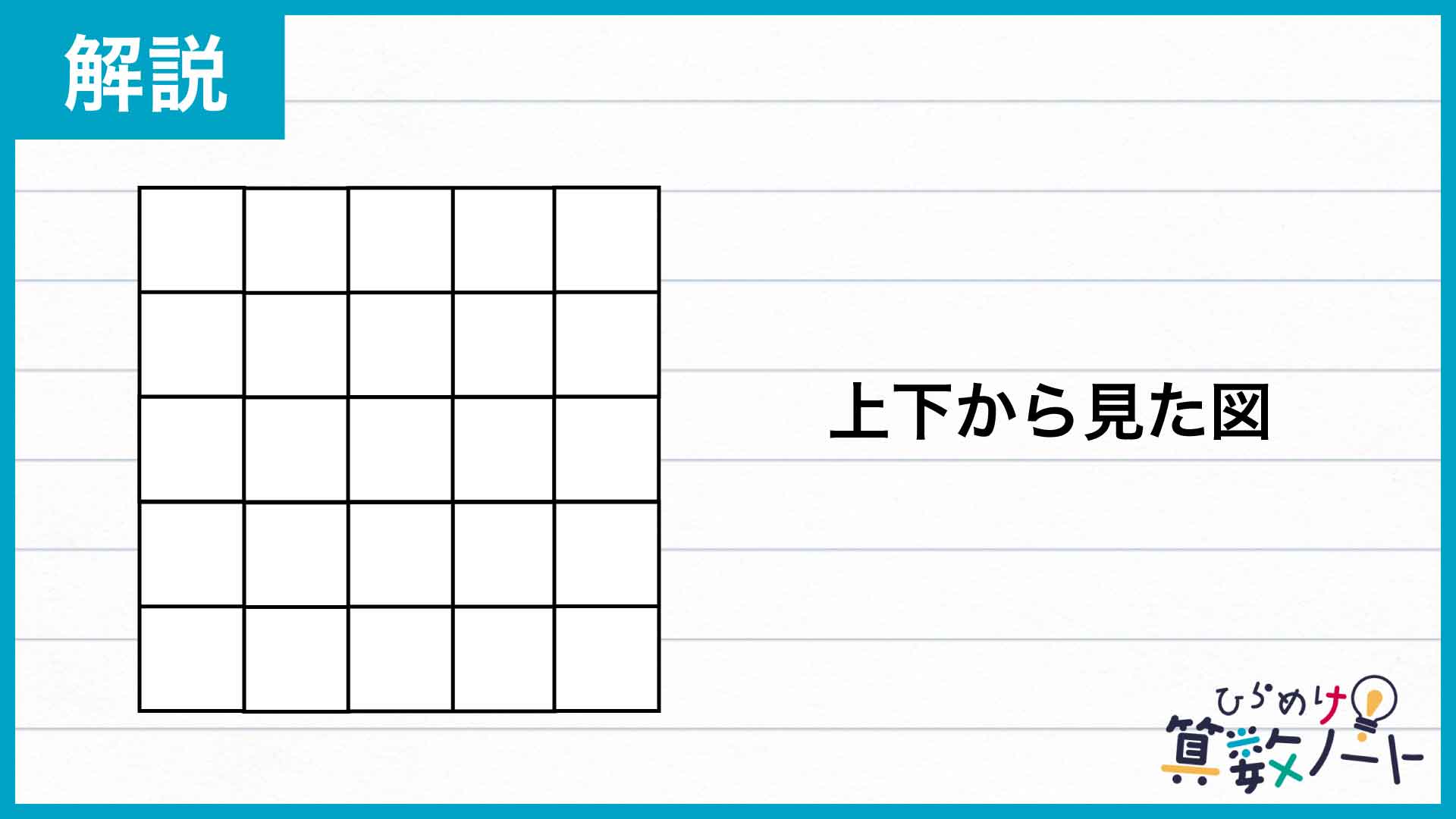
上・下から立体を見る

立体を上・下の2方向から見ると、次の図のように見えます。

先ほどと同じく立体にへこみが無いため、この図形の面積とそれぞれの方向の立体の表面積は同じです。よって、上・下の2方向の表面積は、5×5×2=50cm²となります。

表面積を求める

求める表面積は、前・後・左・右・上・下の6方向から見える立体の面の面積を合計して、36+50=86cm²です。

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】