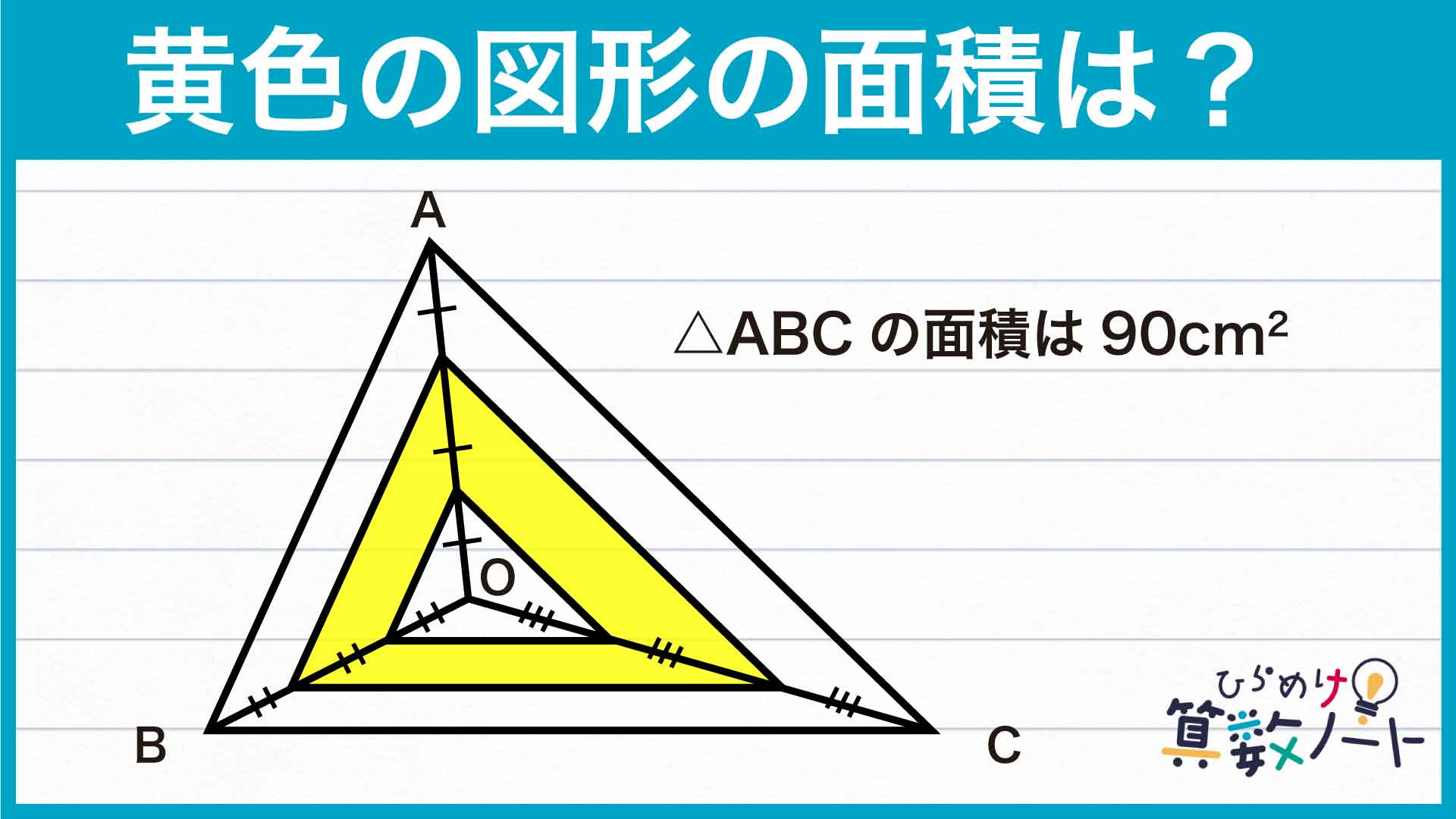
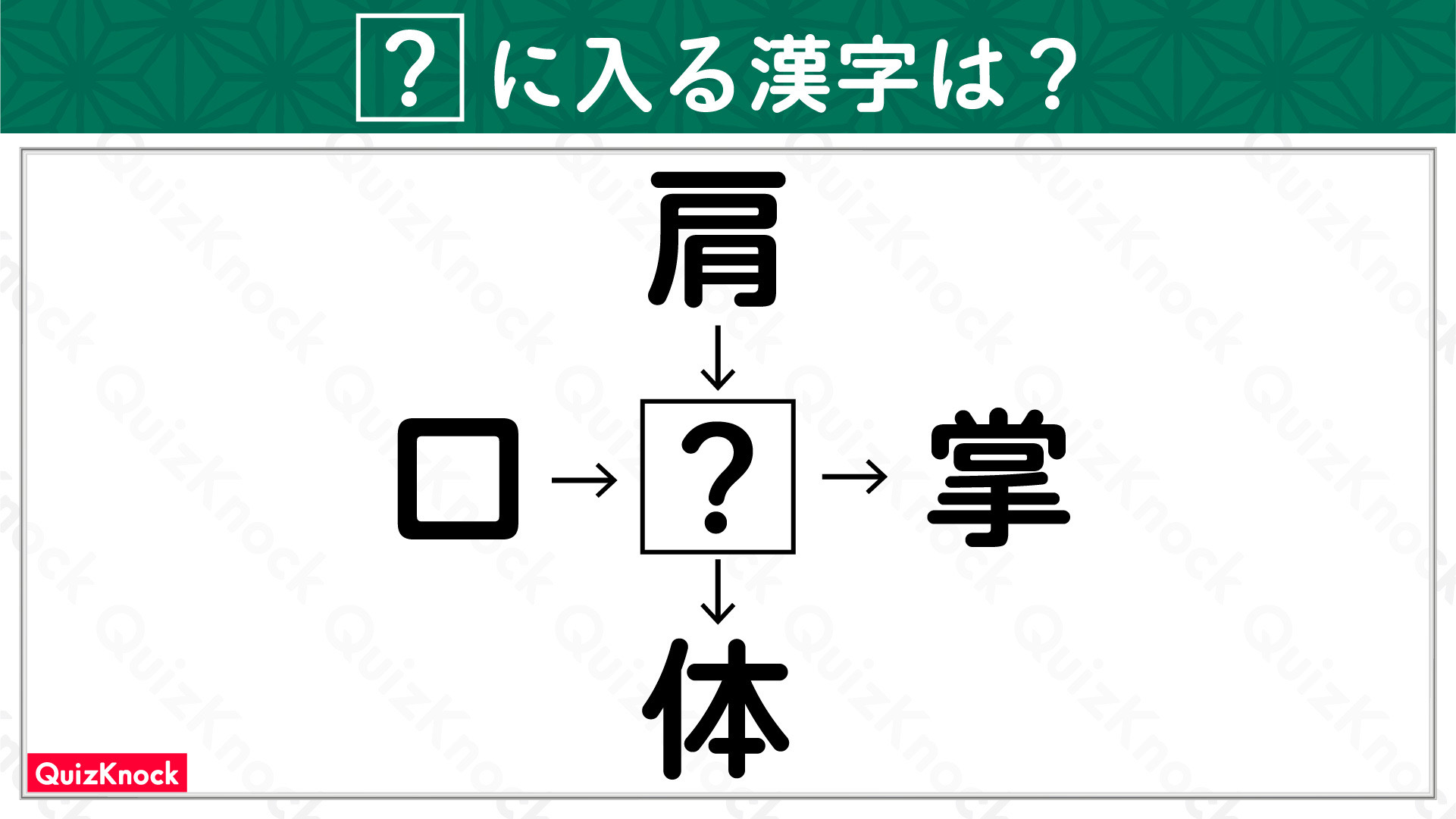
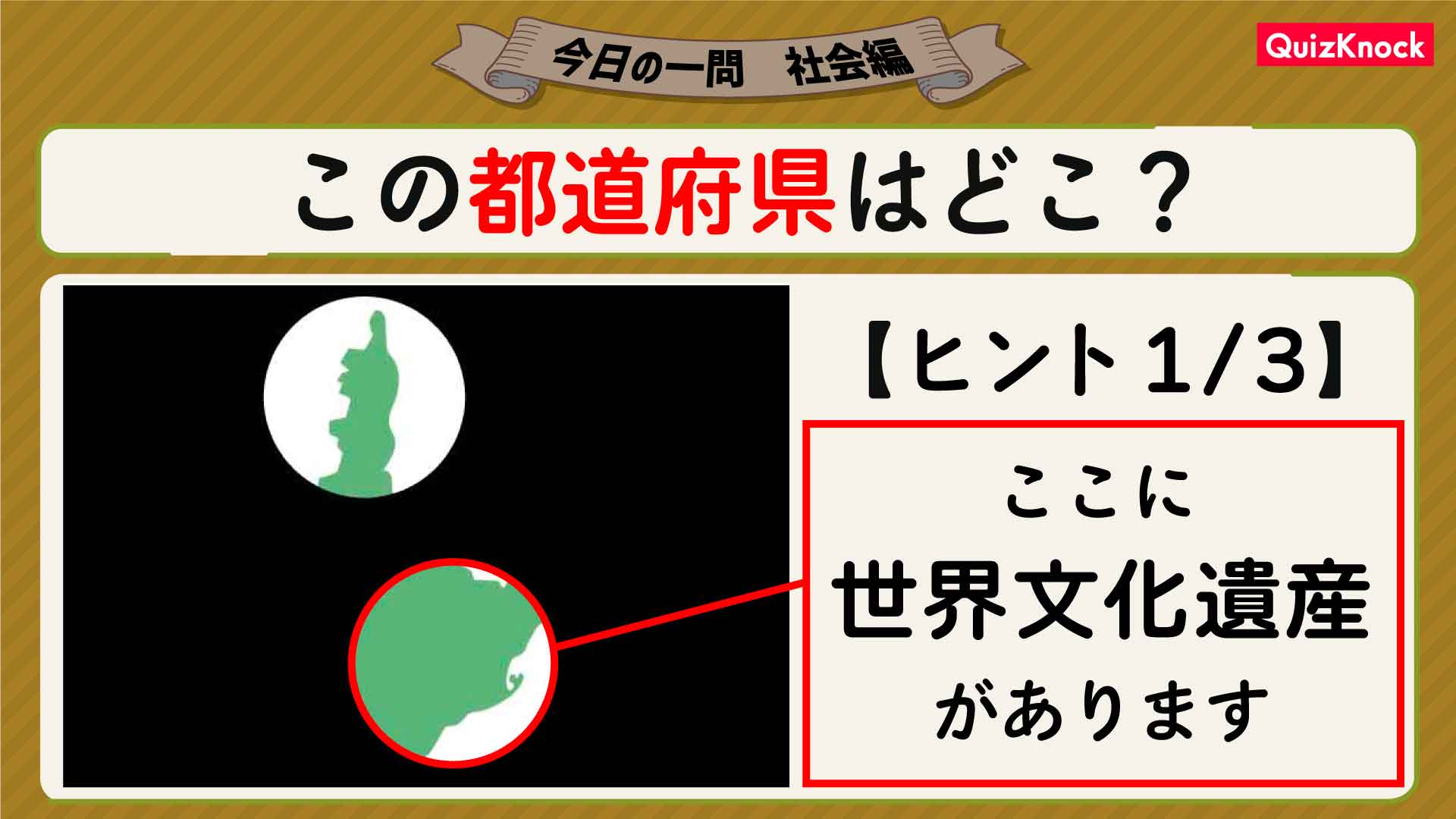
【問題はこちら】
1ページ目:自力で解きたい方はこちらへ!以下は問題の解説です
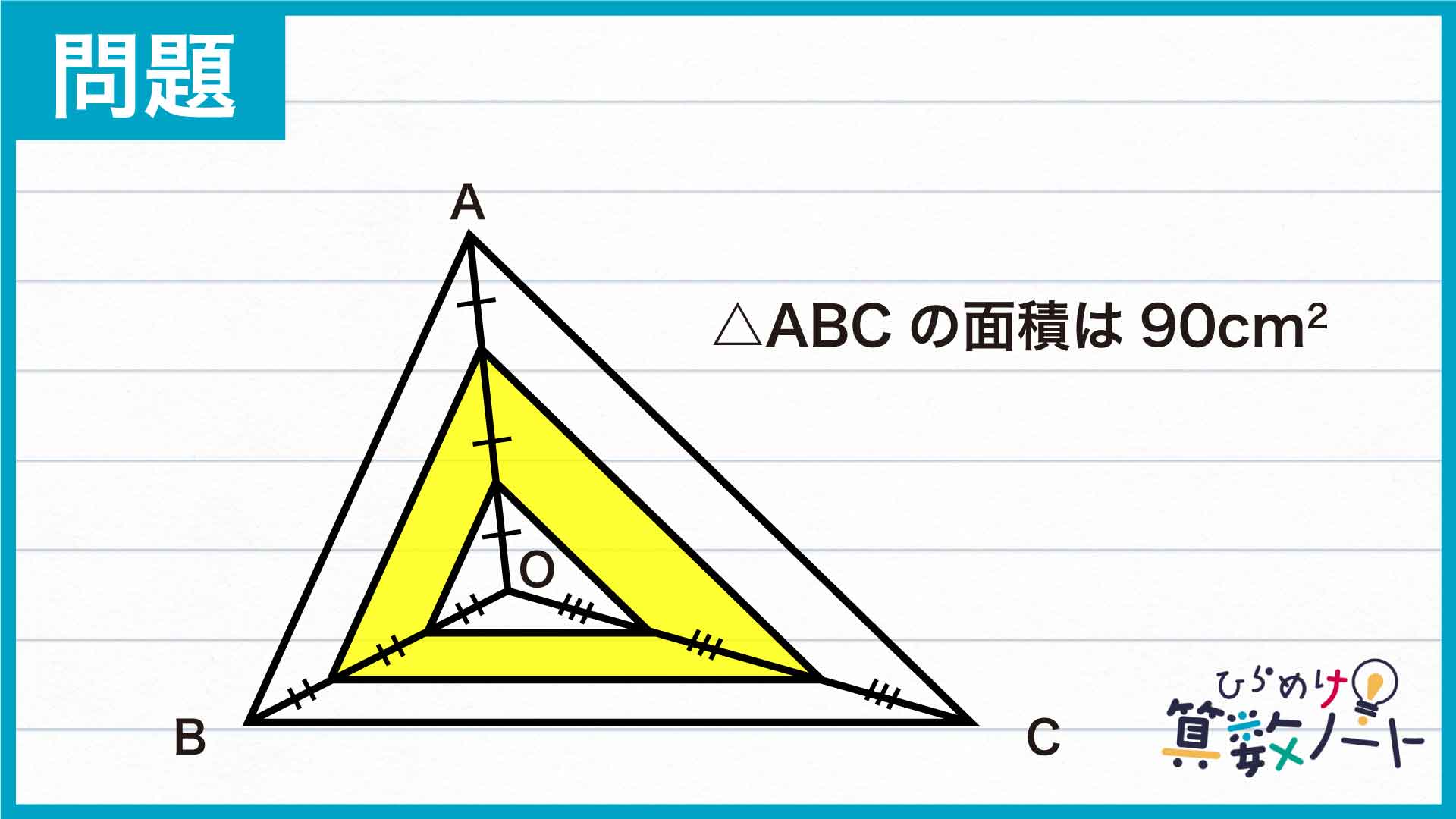
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の問題の解き方をまとめた図がこちらになります。
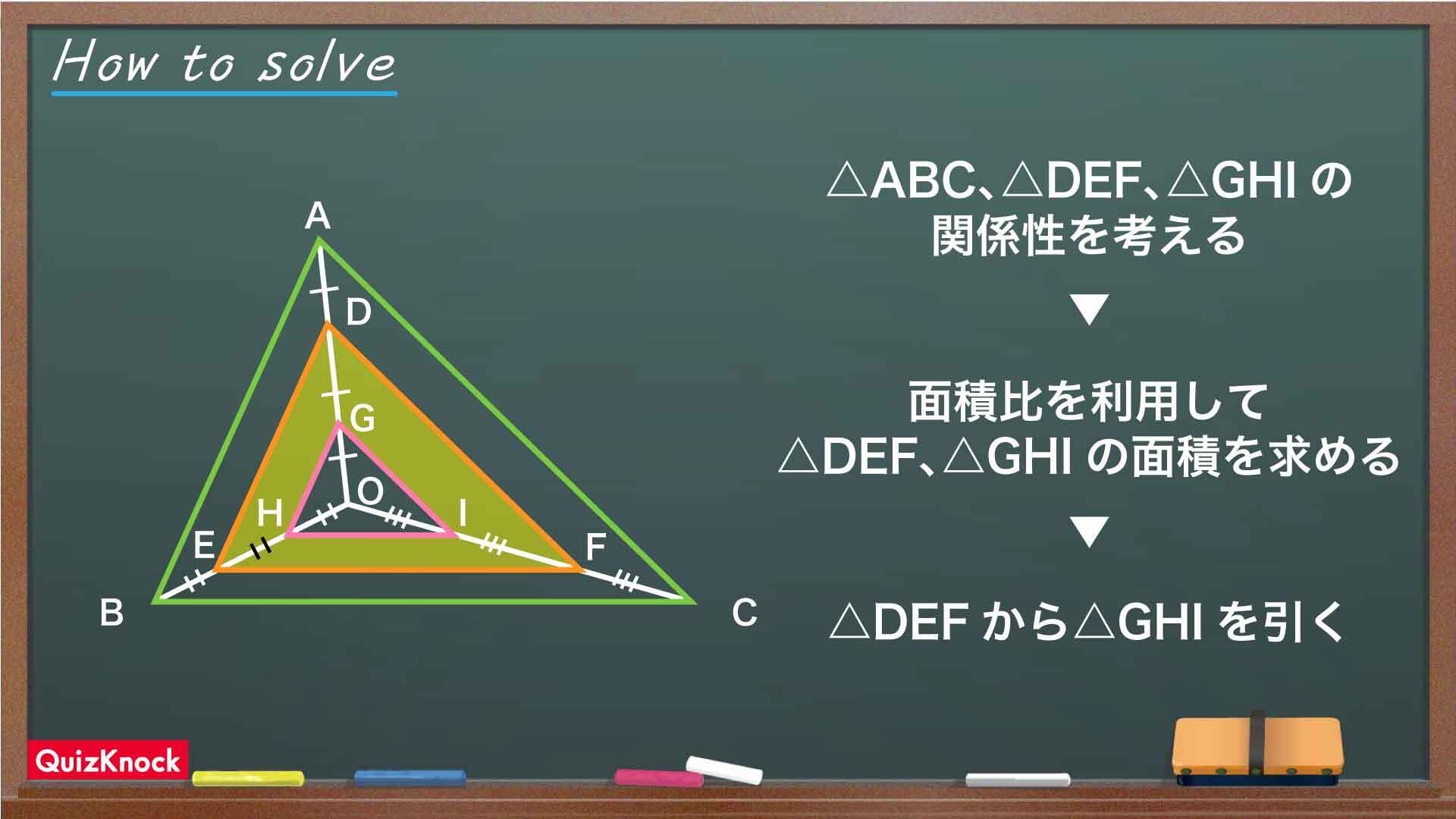
ポイントは、長さが等しい線分に注目して三角形ABC、三角形DEF、三角形GHIの関係を考えることです。これを踏まえて解いていきましょう!
三角形同士の関係を考える
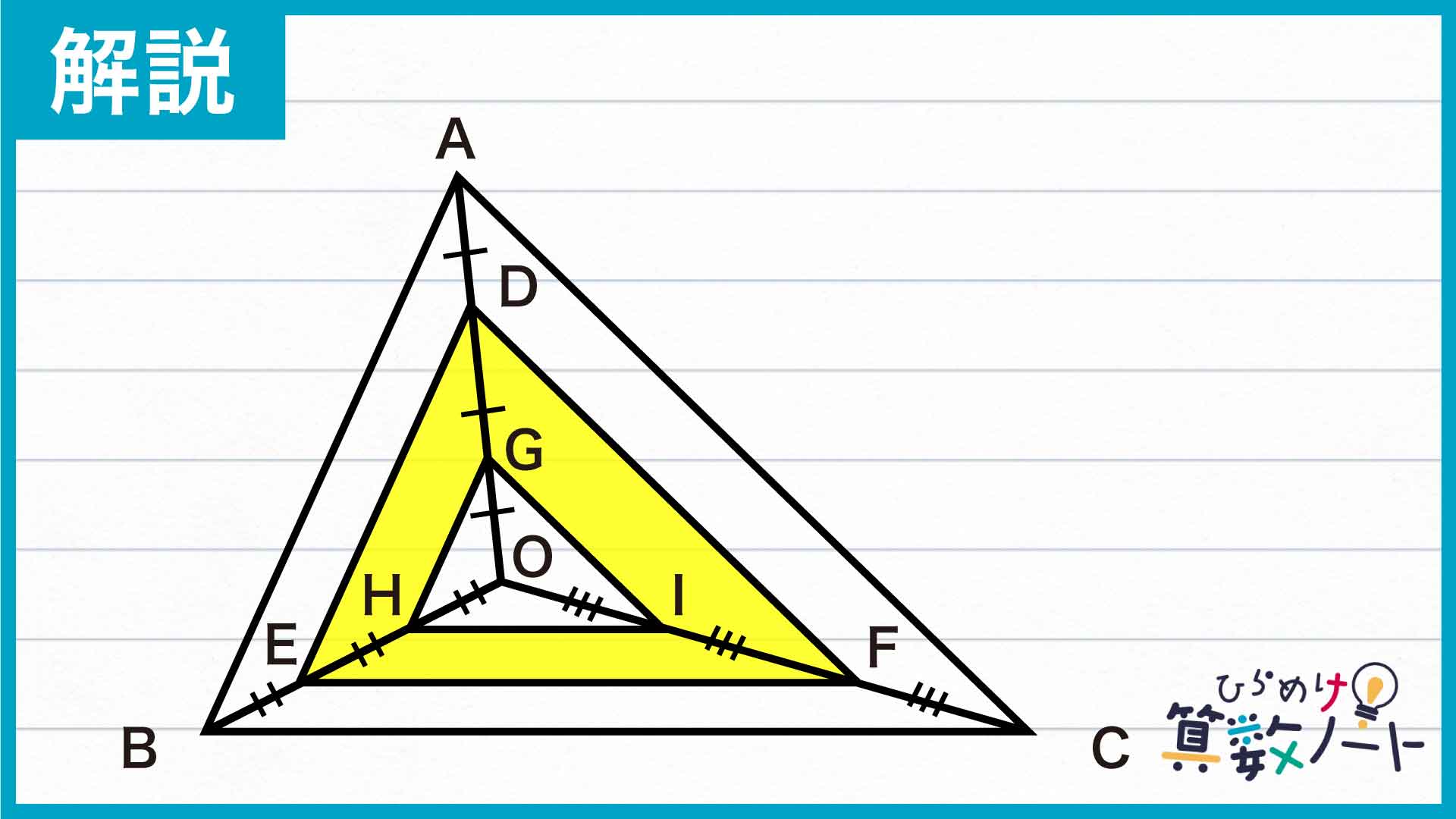
下の図のように、点D、点E、点F、点G、点H、点Iを振ります。
このとき、OG=GD=DA、OH=HE=EB、OI=IF=FCであるため、三角形DEFは、点Oを中心にして三角形GHIを2倍に拡大した図形であることがわかります。
同様に考えて、三角形ABCは、点Oを中心にして三角形GHIを3倍に拡大した図形です。
図形を拡大するとは、ある図形を同じ形のまま大きさを大きくすることを指します。ある図形と、それを拡大した図形については、対応している角の大きさは全て等しく、対応している辺の長さの比はどこでも一定です。
三角形DEFと三角形GHIの面積を求める
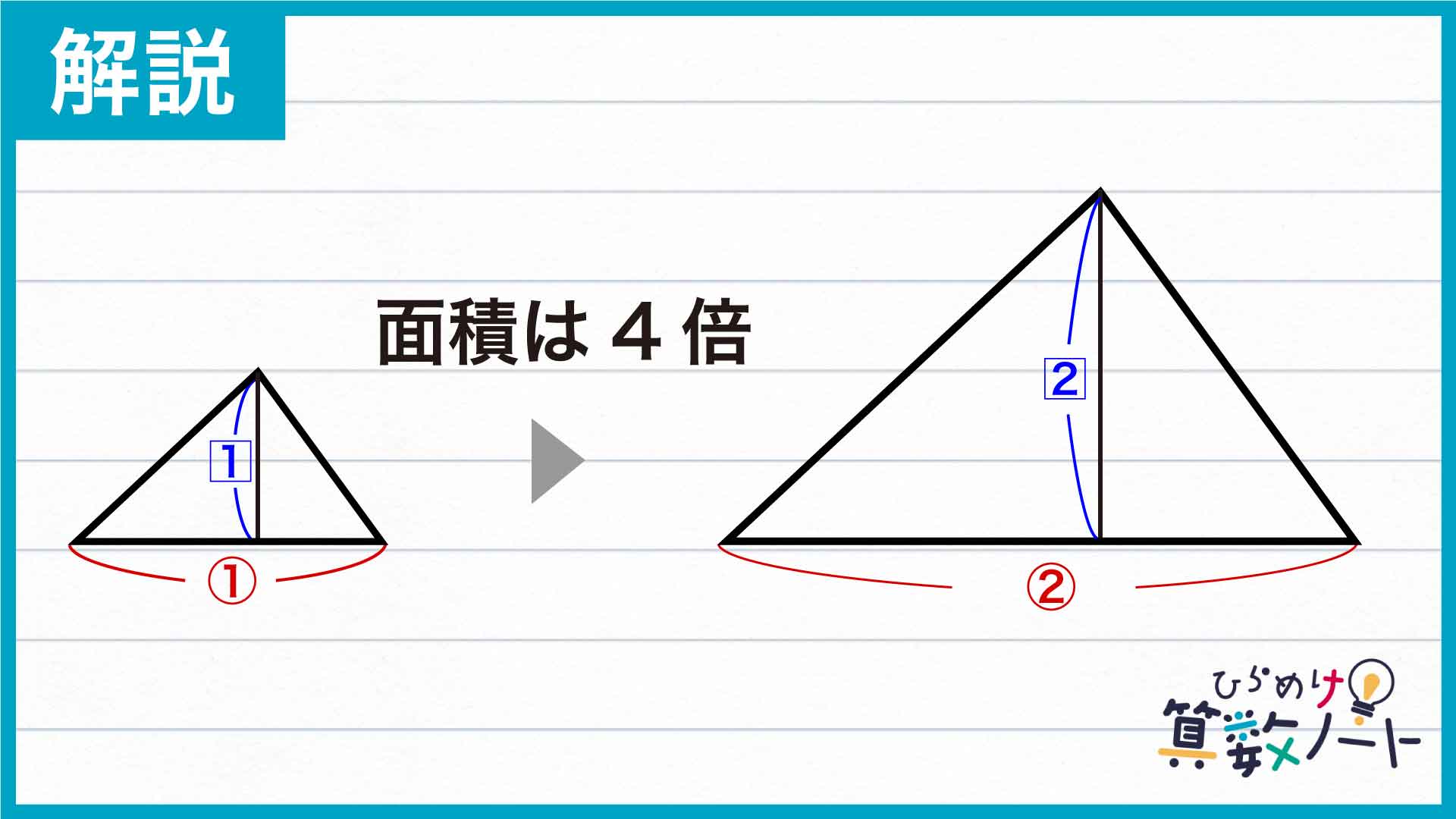
下の図のような三角形を考えてみましょう。右の三角形は左の三角形を2倍に拡大した図形です。つまり、右の三角形は底辺も高さも左の三角形の2倍で、3つの角の大きさは同じです。
三角形の面積は「底辺×高さ÷2」で求めることができるため、右の三角形の面積は、左の三角形の面積の2×2=4倍です。
同様に考えると、ある三角形を3倍に拡大すると、面積は3×3=9倍になることがわかります。
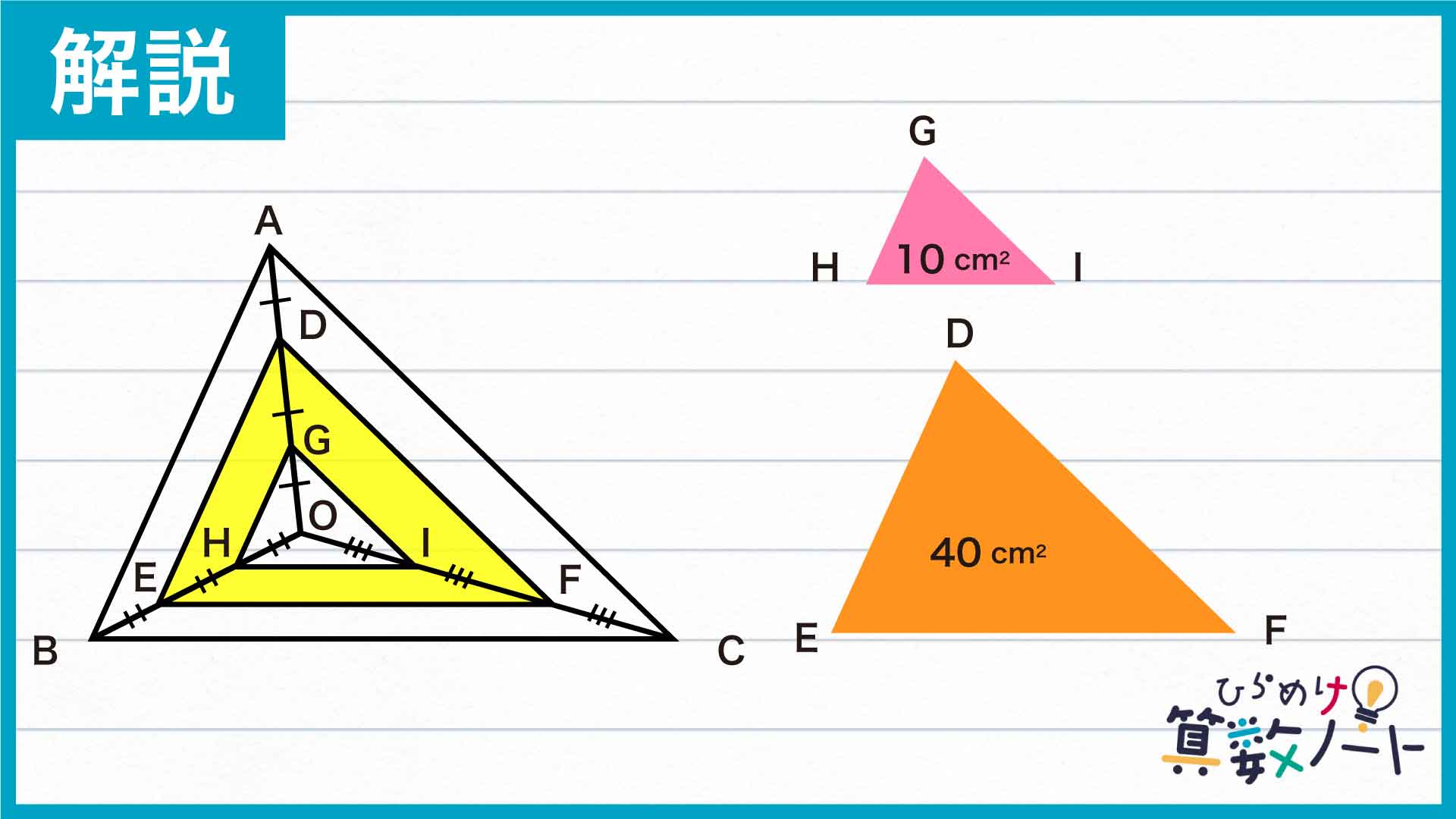
先ほど説明したように、三角形ABCは三角形GHIを3倍に拡大した図形です。三角形ABCの面積は90cm2なので、三角形GHIの面積は90÷9=10cm2となります。
また、三角形DEFは三角形GHIを2倍に拡大した図形なので、三角形DEFの面積は10×4=40cm2です。
黄色く色を付けた図形の面積を求める
ここまで来ればあとは簡単です。黄色く色を付けた図形は、三角形DEFから三角形GHIをくり抜いた図形なので、その面積は40-10=30cm2です。
答え:30cm2それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)






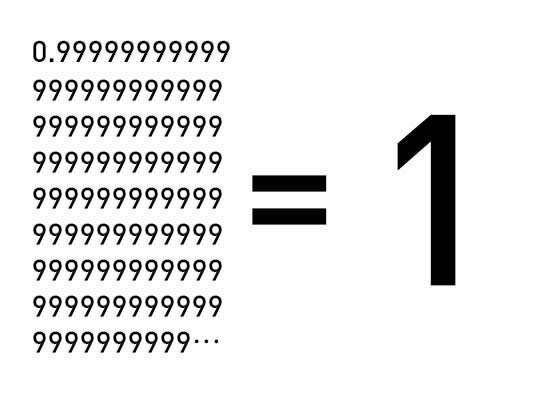
.jpg)






