解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです。
今回のポイントは、「同じ長さの線を探す」ことです。
色をつけた六角形の辺の長さを、1本ずつ求めるのは不可能です。そこで、発想の転換が大事になります。
六角形の各辺の長さを直接求められないのであれば、同じ長さをもつ別の辺に移動させ、長さが求まる線へと変形させます。
これにより、色をつけた六角形の周りの長さを間接的に求めることができます。
以上を踏まえ、問題を解いていきましょう!
正三角形を見つける
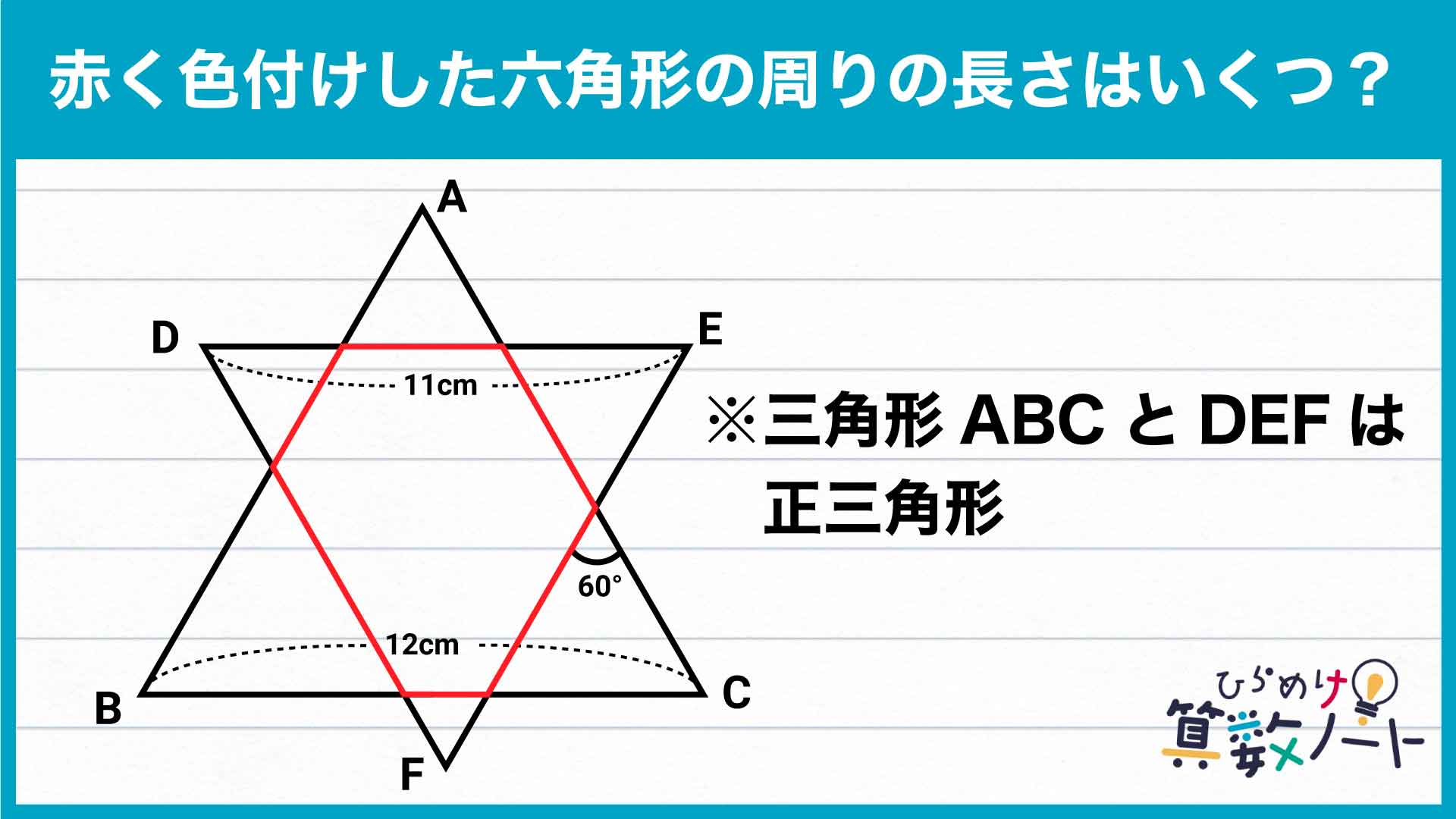
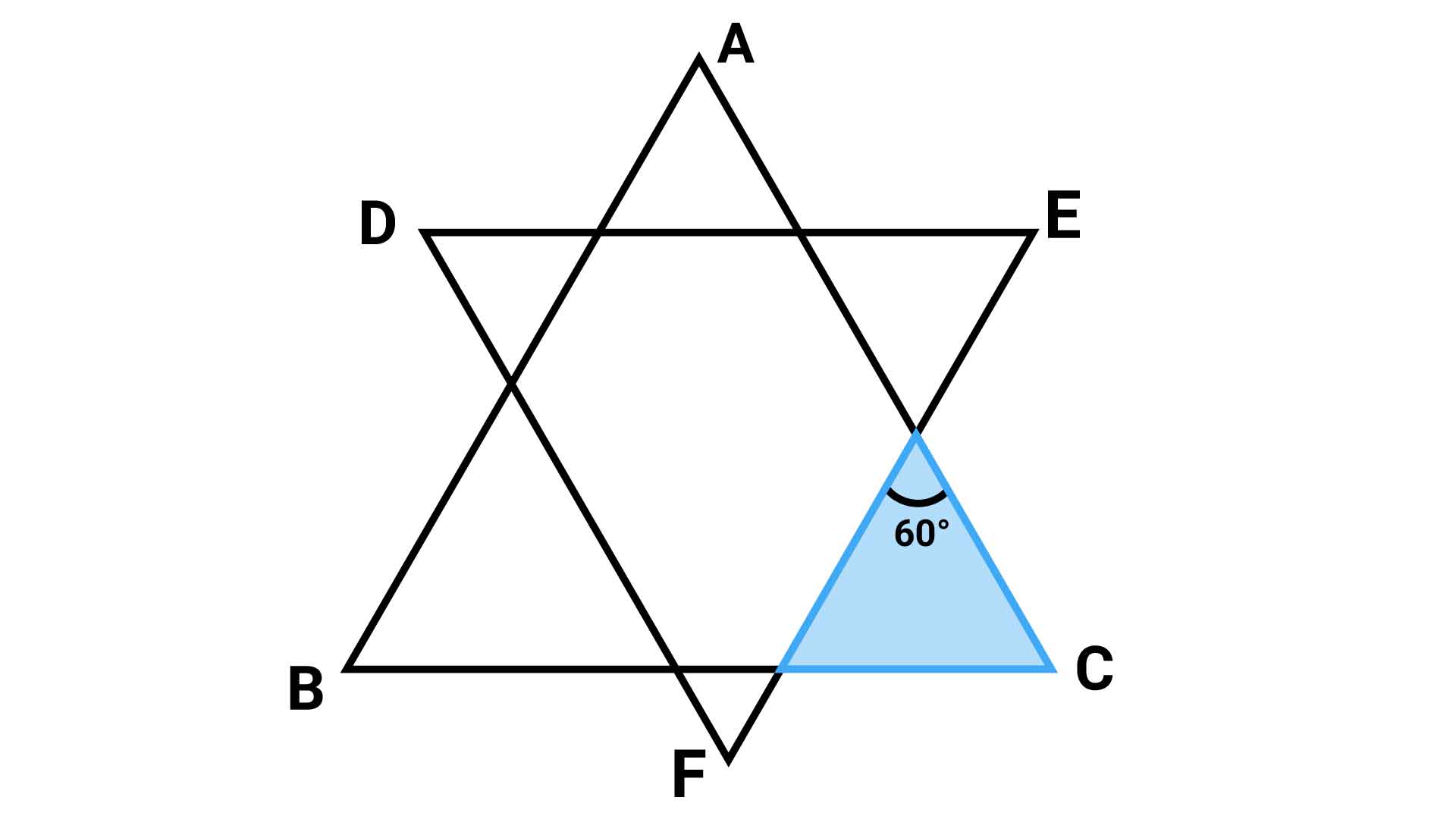
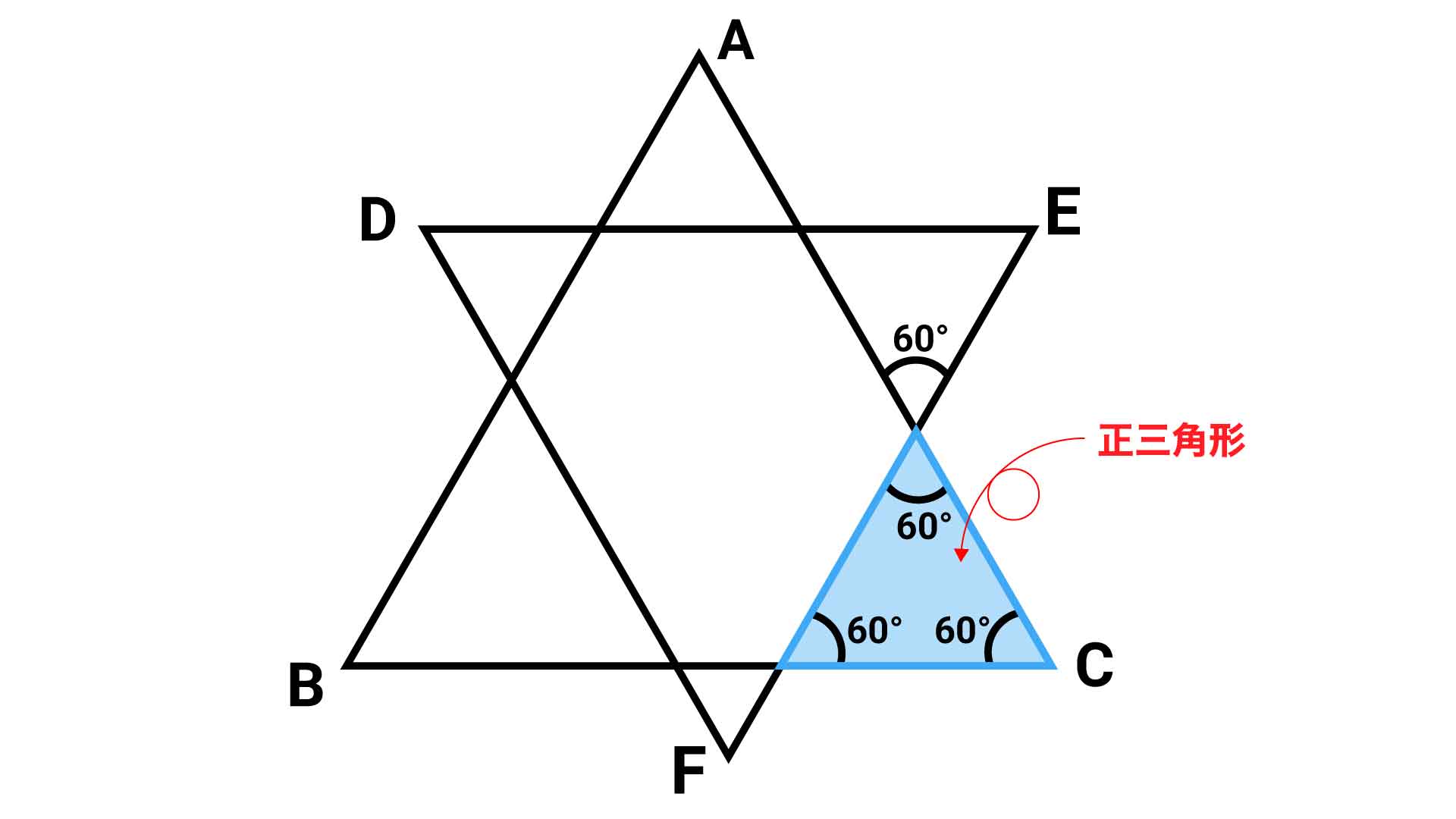
まず、右下の小さな三角形に注目します。
この三角形の3つの角のうち、1つの角の大きさはすでに60度と与えられています。そして、もう1つの角は1辺12cmの正三角形と共有しているので、角度は60度になります。したがって、残り1つの角の大きさは180-(60+60)=60度となります。
全ての角の大きさが等しいため、この三角形は正三角形であることがわかります。
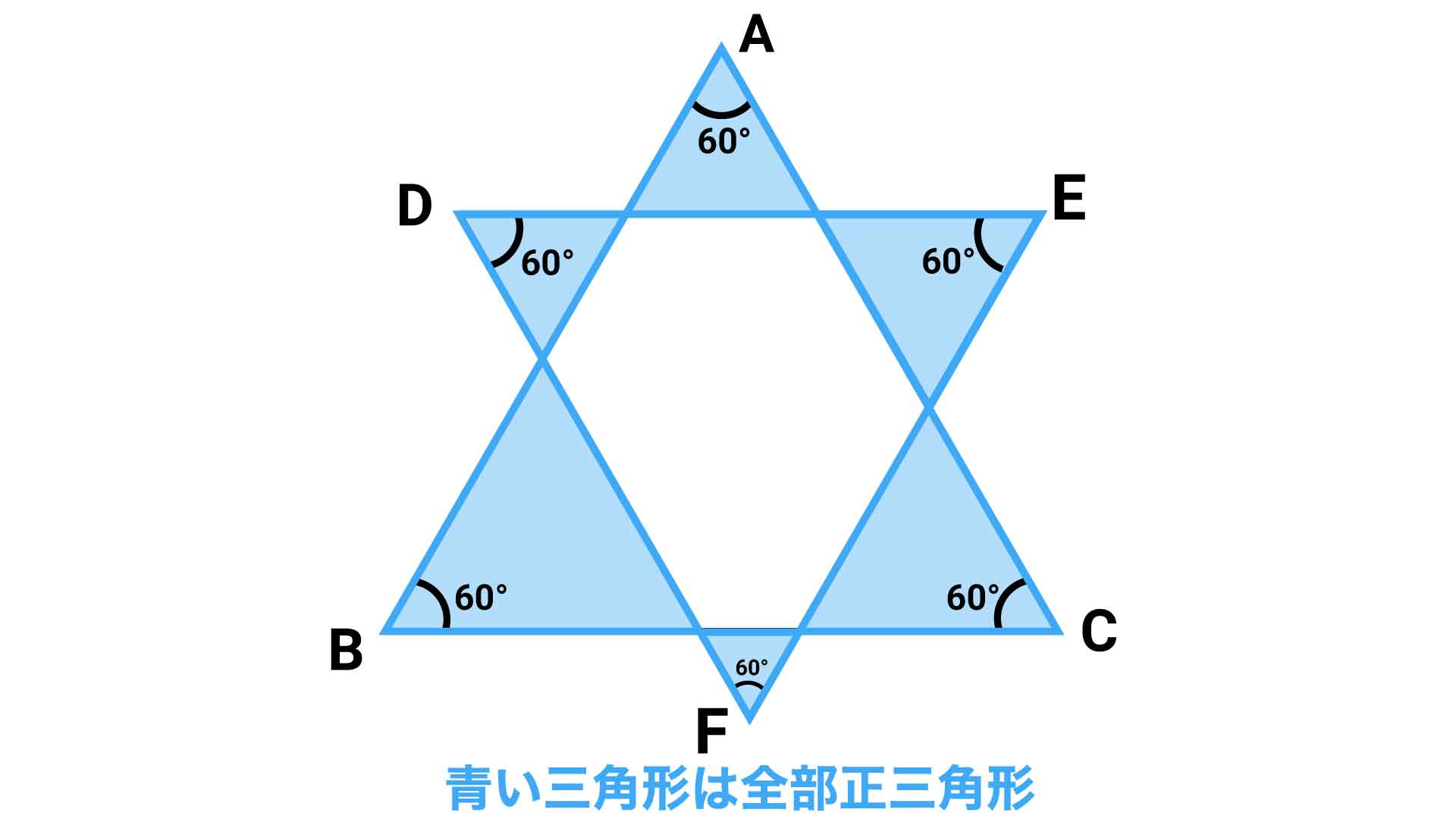
そして、60度の角と向かい合っている角の大きさもまた60度となります。同様にして順に角度を求めていくと、六角形の周りに並んでいる6つの小さな三角形全てが正三角形であることがわかります。
長さが等しい辺を移しかえる
正三角形では、3本の辺の長さは全て等しくなります。この性質を使えば、長さの等しい辺同士を入れかえて、六角形の輪郭を変形させることが可能です。
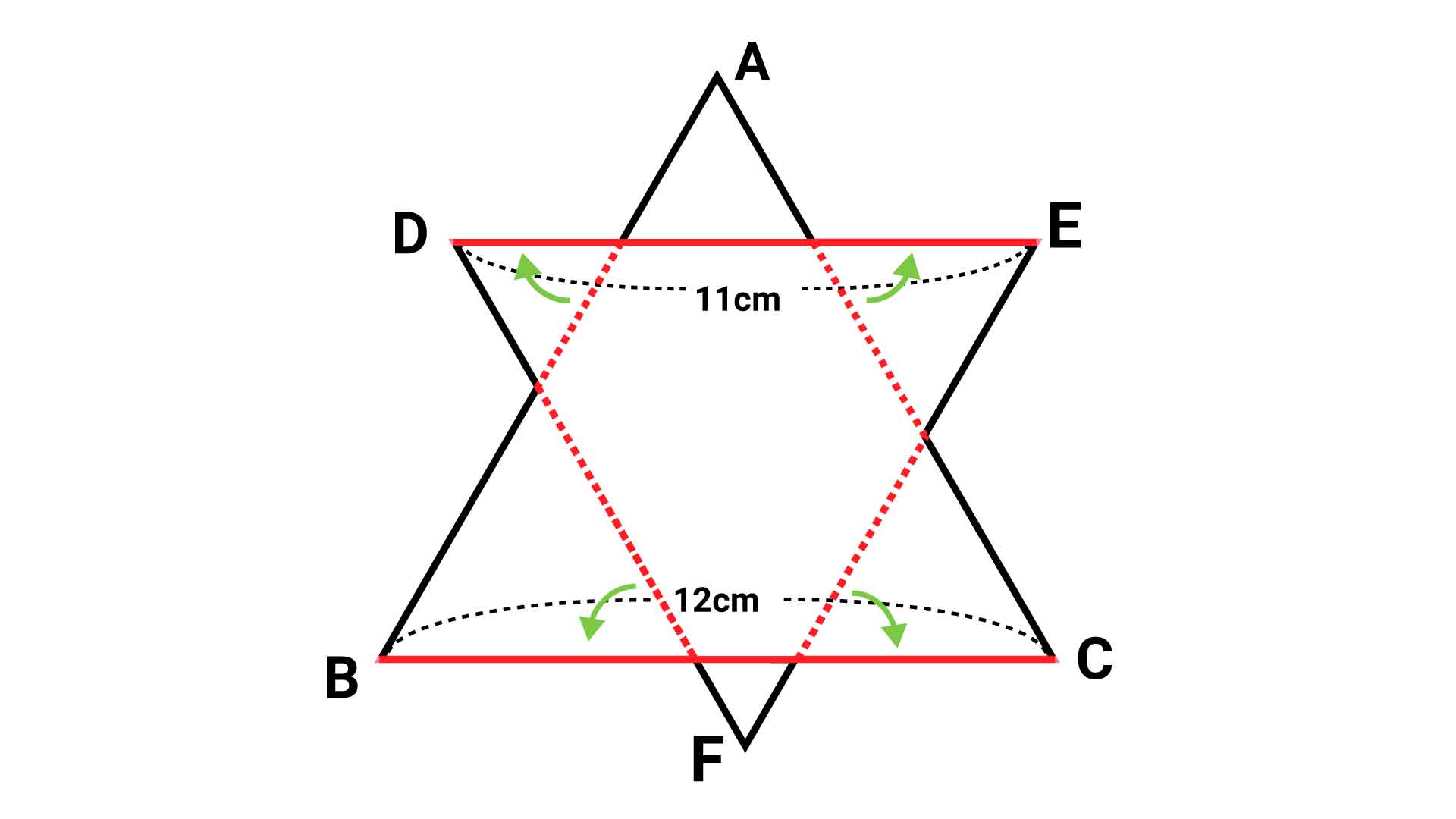
今回は、大きな正三角形の辺の長さが11cmおよび12cmと与えられていますので、これらの辺の上に並べるようなイメージで線を移動させていきましょう。
これにより、六角形の周りの長さは、1辺が11cmおよび12cmの正三角形の辺1本ずつと等しいということがわかります。
よって、求める長さは11+12=23cmとなります。
答え:23cm
またの挑戦をお待ちしています!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)








.jpg)