どうも、カワカミです。
先日、東京大学の前期日程試験・第1次選抜の合格者が発表されました。これは二次試験の受験者を、センター試験の点数によって選抜するものです。
その中では合格者の最高点・最低点・平均点が明らかにされているのですが……、な、な、なんと、ついに出てしまいまったのです。そう、センター試験で満点を取った受験生が……！
勘でイケるんじゃね？
ご存知のとおり、センター試験はマークシート式の試験。マークシートを埋めたことがある方なら、一度は思ったことがないでしょうか。
「この問題分かんないけど、テキトーに塗ったら当たらないかなあ……」
理論上、可能性はあります。選択肢が4つだった場合、その問題に関しては4分の1の確率で当たることでしょう。分からなかった問題が4問あったならば、期待値で考えるとそのうち1問は当たるのです。
……でも思いませんか？
1問じゃ足りない。
分からない問題も、全部勘で当てたい！
僕もセンター試験で満点が取りたい！！！
どれくらいの確率で満点が取れるか、考えていこうじゃありませんか。
いきなりですがアナタはセンター9割取れます（仮定）
今回受けてみるのは、2018年度のセンター試験・本試。満点が出た、今年の試験です。
あなたは、東京大学理科一類を目指す受験生です。受験する科目は、国語・英語・数学IA・数学IIB・物理・化学・地理Bとしましょう。国語と英語は200点満点、他は100点満点ですから、900点満点です。
まさか右も左も分からない状態ではセンター試験に挑まないでしょうから、あなたは理科一類に受かる見込みがある実力を持っているものとします。具体的には、センター試験で9割が取れるレベルです（第1次選抜合格者の平均点は802.00点なので、東大受験者の平均よりちょっと上、程度です）。簡単のため、全教科ちょうど9割の点数が取れるとします。
つまり、あなたは今から、残りの1割・90点分を勘だけでもぎ取らなければいけないのです。果たして。
わずか90点だが……
・国語（200点）
200点満点中、あなたは180点を取る実力は持っています。全国平均が100点強のテストですから、180点も取れば十分な気もしますが、今目指しているのは200点。20点分を強運で強奪していきましょう。
国語は1問あたりの配点がかなり大きい教科。まずはちょうど180点を取るために、第2問・問4、第3問・問1（ウ）、第4問・問4の3問を間違えたとしましょう。それぞれ配点は8点、5点、7点。いずれも5択の問題です。
5択の問題3問が、勘で全て当たる確率は、1/5の3乗＝1/125。百分率に直すと0.8％です。ガチャに脳を冒された方なら「回せば出る」といった数値でしょうか。残念ながらセンター試験ガチャは1年に1回しか引けませんが、可能性がないわけではない、といったところですね。
・英語（200点）
国語同様、英語も180点までは確約されています。実際の受験生にとっては羨ましいことこの上ない話ですね。
さて、残りの20点ですが、国語に比べて1問あたりの配点が低いため、5問必要となりました。
4択の問題：第1問B・問3、第2問A・問9、第4問B・問2、第6問A・問5と、8択の問題：第2問C・問2の合計5問が、勘で全て当たる確率は、1/4の4乗×1/8＝1/2048。百分率に直すとおよそ0.05％。国語と比べるとかなり厳しくなってしまいました。
・数学IA（100点）
このチャレンジにおいて、鬼門となるのが数学です。何故なら、解答となりうる選択肢が多すぎるのです。たとえば、第1問のソ・タは下図のような形で表されます。
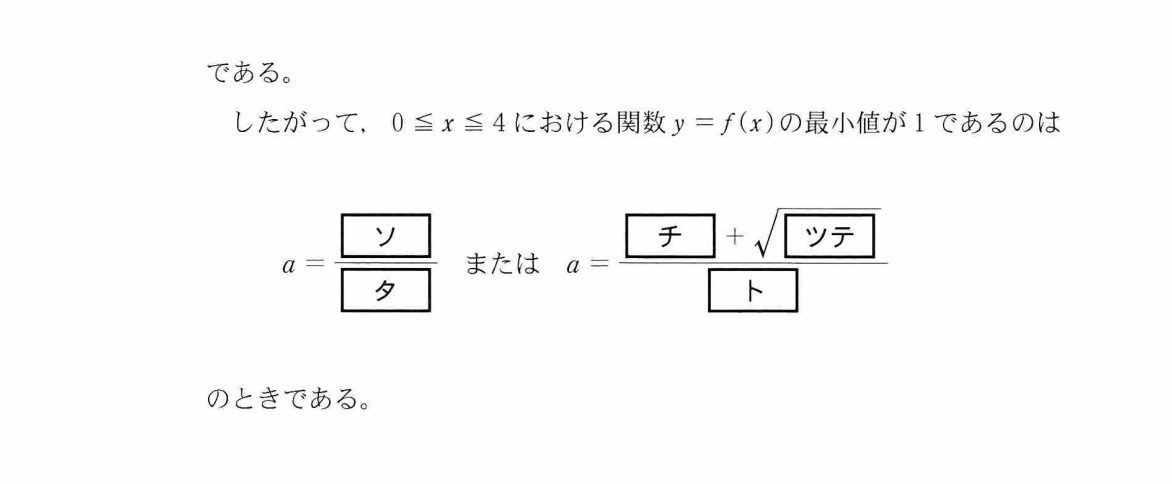img Via 朝日新聞デジタル
このソとタは完答が求められるため、1問あたりの勘で正解できる確率がぐんと下がります。
わざわざ分数で表されているのだからタ＝1はありえないとか、ソとタは互いに素のはずだとか、本来はいろいろ考えなければいけないポイントはありますが、今回は全部無視。一括で0～9の10択にしてしまいます。何故なら、今回の趣旨は「勘だけで」正解すること。そもそもそんなこと考えてる暇があるのなら、真面目に解いた方が絶対に良いし。
ということで、このソ・タを勘で正解できる確率は、1/10の2乗＝1/100。ちなみに、この問題の配点はたった2点。90点は既に取れていますから、あと8点……。
ここからダイジェストで参ります。
今回の誤答：第1問ソタ、チツテト、第3問チツテ、第4問セソ
勘で全て当たる確率：1/100×1/10000×1/1000×1/100＝1/100000000000（1千億分の1）
・数学IIB（100点）
今回の誤答：第2問トナニヌ、第3問ソタチ、ナニヌネ
勘で全て当たる確率：1/10000×1/1000×1/10000＝1/100000000000（1千億分の1）
・物理（100点）
今回の誤答：第1問・問3、第5問・問3
勘で全て当たる確率：1/8×1/8＝1/64（約1.5％）
・化学（100点）
今回の誤答：第2問・問3b、第3問・問3、第4問・問5b
勘で全て当たる確率：1/6×1/4×1/5＝1/120（約0.8％）
・地理B（100点）
今回の誤答：第2問・問４、第3問・問5、第5問・問5、第6問・問2
勘で全て当たる確率：1/4×1/4×1/4×1/4＝1/256（約0.4％）
いよいよ合格発表！
さて、各教科で満点を取る確率が求まりました。これらを全てかけて、「センター試験満点」の栄誉を勘だけで獲得できる確率を求めてみましょう。
1/125×1/2048×1/100000000000×1/100000000000×1/64×1/120×1/256≒5×10の33乗分の1＝50溝（こう）分の1
こ、溝……。使い慣れない単位が出てきてしまいました。とりあえず50溝浪すれば、1回くらいはセンター試験で満点を取ることができそう、ということですね！
50溝……ナンボ？
ちなみに、人類誕生から現在までが、約1兆7000億日。現在の人類70億人（全員が理科一類志望で、もともとセンター9割取れると仮定）が地球誕生から現在まで2日に1セットずつ解いたとしても、満点が出る可能性は約1兆分の1。1兆個のパラレルワールドに訴えかけるしかない……！
もう一つ例え話を。地球上には、約30溝体の生物がいるらしい。つまり、今この瞬間地球上の全生物のなかに1体だけ「大当たり」生物がいるとして、それを見つけ出すくらい大変なのです。
その当たりはアナタかもしれないし、アナタの布団に居るダニかもしれないし、上野にいるパンダかもしれないし、さっき飲みこんじゃった菌かもしれない。それがたまたま当たりの可能性が30溝分の1で、センター満点はそれを見つけ出すより1.7倍くらい大変なんです。ヤベエ。
結論
無理！せめて数学だけでも自力で満点を取ろう！！！
