伝説の東大数学は算数で解ける【1998年後期】

不可能であることを証明する！？

次に、nを3で割った余りが2のときに、n(=3m+2)が条件を満たさないことを証明します。つまり、〇を2,5,8,……個並べられないことを示します。

「できる」ということを証明するときは、たくさんある〇の追加法のうち、1つでも具体的な方法を見つけられれば良いことが多いです。

しかし「できない」ということを証明するには、たくさんある〇の追加法のうち、どの方法でもできないということを言わなければなりません。〇の追加法を全通りやってみて、どの場合でも〇がn個並ばないことを確かめることができれば良いですが、今回はnが増えるごとに追加法が爆発的に増えていき手に負えないため、この方法は使えません。

さらに、〇や●の数の変化を考えるだけではなかなかうまくいかないというのがこの問題の恐ろしいところ。では一体どうしたらいいのか……。

【アイデア1】四角いオセロの石を2つ用意し、最初は白い面を上に向けて両端に置く

最初から両端に四角いオセロの石を1つずつ置いておきます。つまり、「〇」ではなく「□〇□」を初期状態として考えます。

例えば、

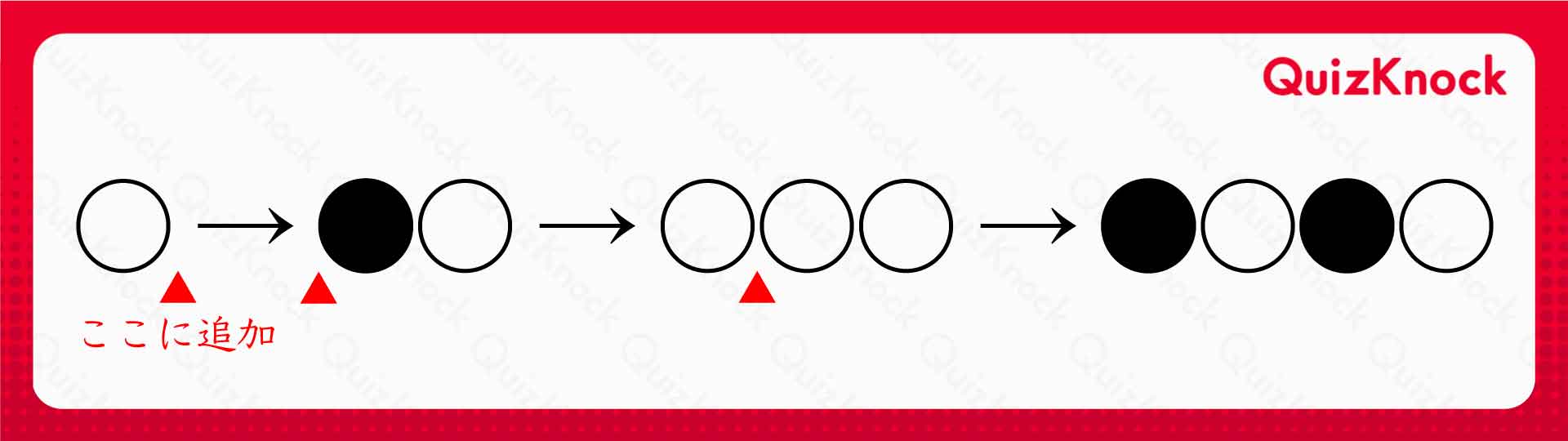
という一連の操作を考えます。初期状態の両端に□を加えておくと、石の色の変化は

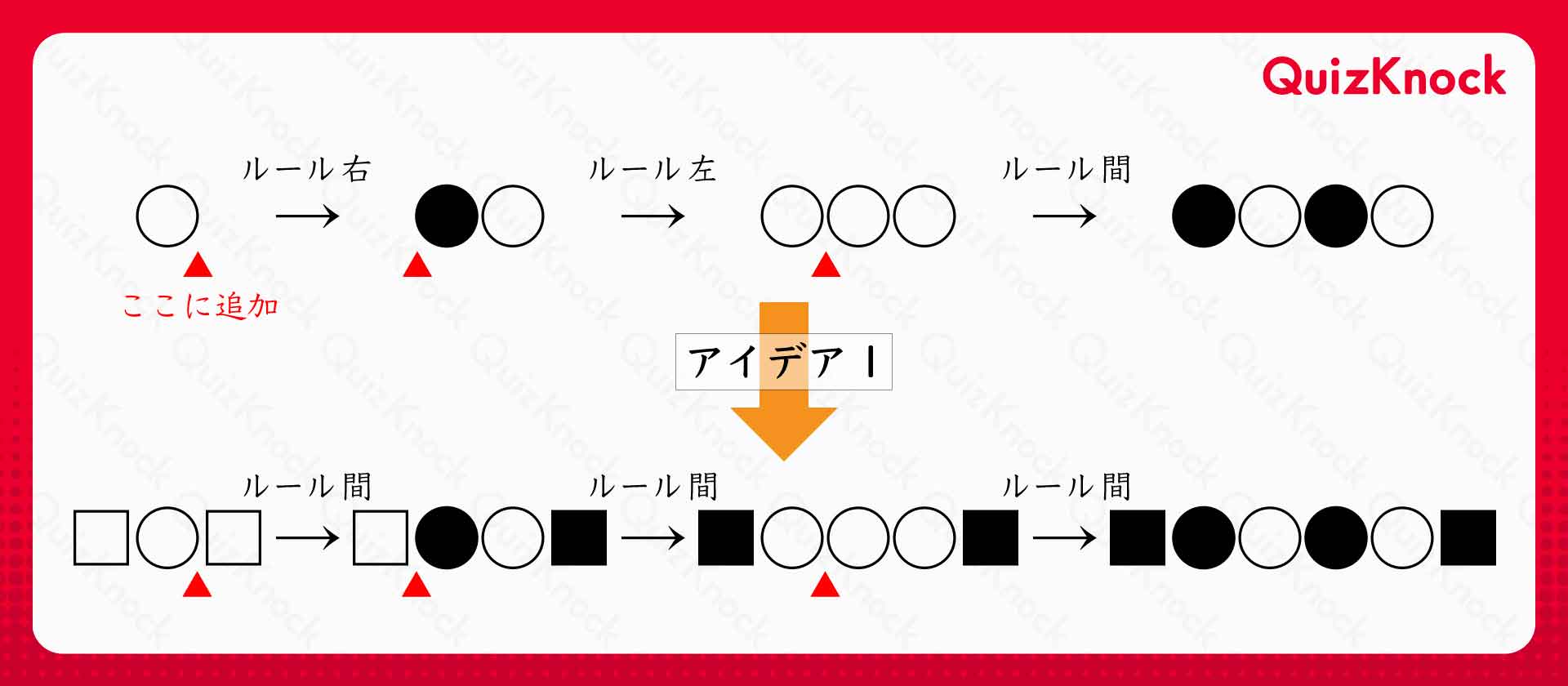
となります。このとき、四角い石も裏返ることに注意してください。

両端の四角い石を無視すれば、両者は一致します。つまり、アイデア1を適用した後は、「□〇〇…〇〇□」「□〇〇…〇〇■」「■〇〇…〇〇□」「■〇〇…〇〇■」がどれもできないことを証明すれば良いです。

また四角い石の外側に石は追加されないので、アイデア1を用いるまではルール右・左だったものも、すべてルール間になっています。アイデア1を用いることによる違いをまとめると、次のようになります。

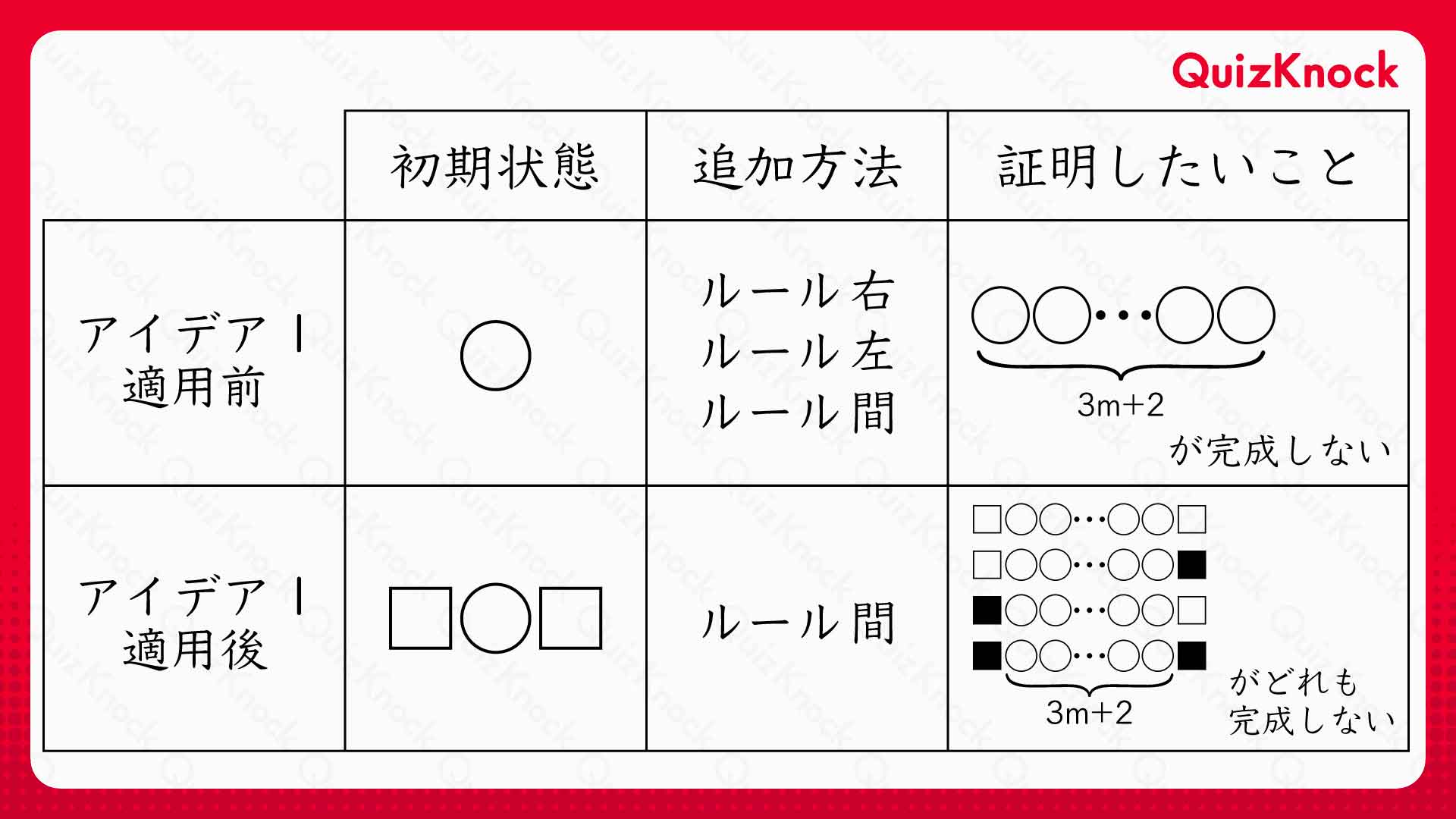
【アイデア2】並んでいる石の上に、ルールに従って×印が表示されるようにする

「その石より左にある石（その石自身を含む）の中に、黒石（●・■）が奇数個あれば×印をつける」というルールを導入します。

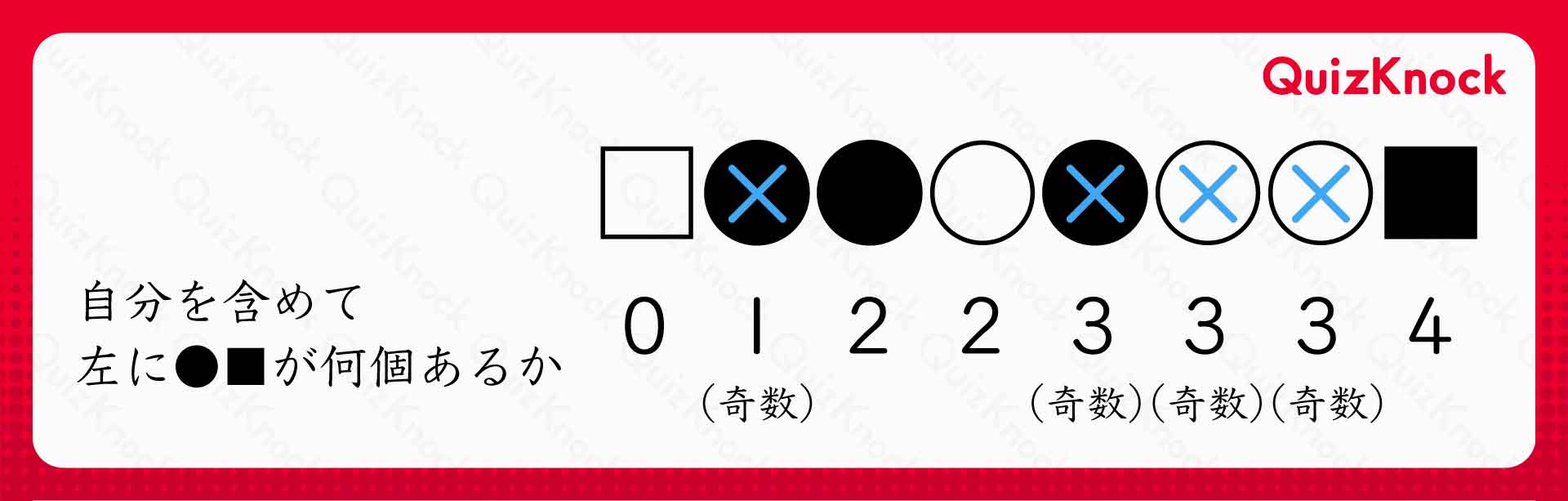
×の増え方の規則性を見つけよう！

〇を追加していく様子を、アイデア1,2を用いて観察してみると、以下のようになります。

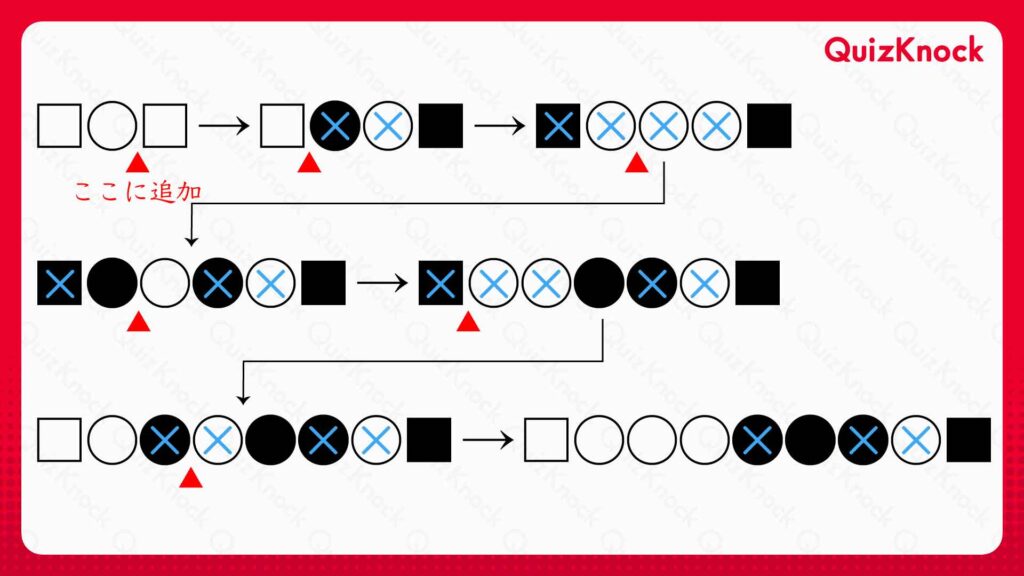
×の数の変化に注目してみると、〇を1個追加することで全体の×の数は「2増える」または「1減る」のどちらかだと予想できます。実際、これは成り立ちます（※2）。

これを確かめるために、〇を1個追加するときの×の変化を以下の図のように3つのブロックに分けて観察します。

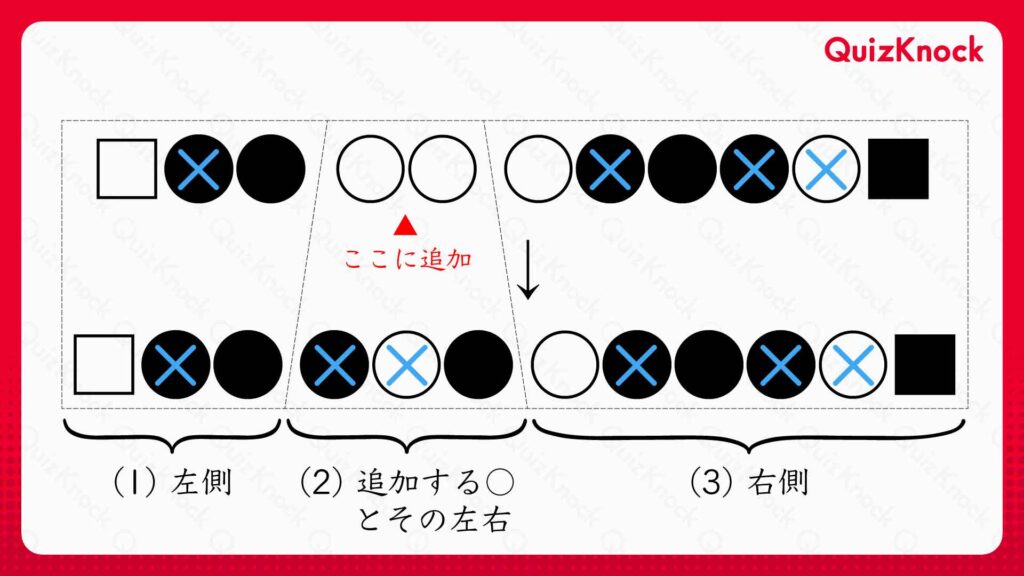
まず、(1)左側のブロックについて考えます。×の数はその石を含めて左にある●や■の数に変化があった場合のみ変化するため、〇を追加しても(1)左側の×の位置に影響はありません。

次に(2)追加する〇とその左右の石についてです。追加前の〇・●・×の組み合わせを考えると、以下の8種類しかないことがわかります。

これらに〇を1個追加すると、

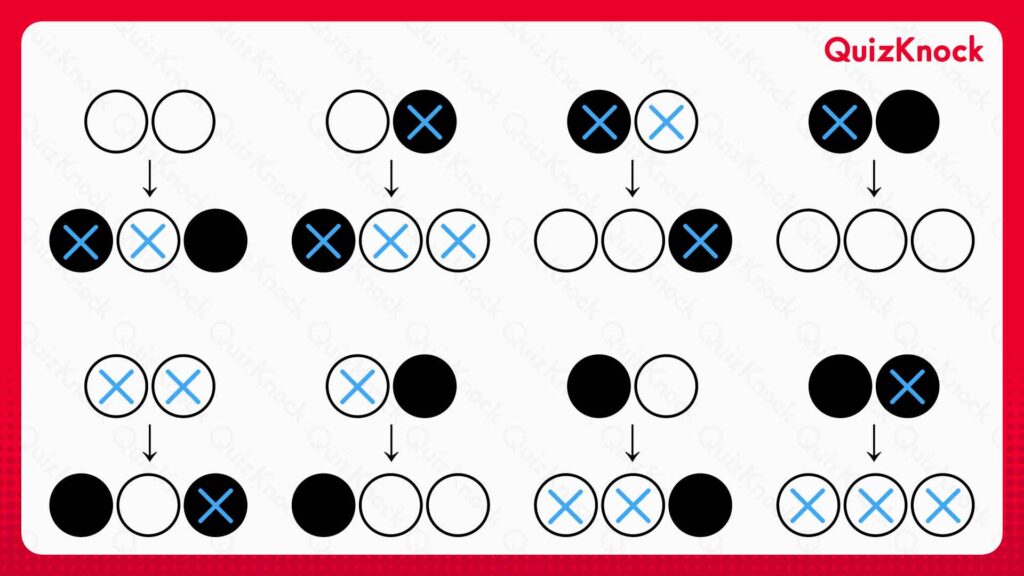
のようになるので、(2)に含まれる×の数は、必ず「2増える」または「1減る」のどちらかであることが確かめられます。

また○の追加前後で、(2)に含まれる●・■の数が奇数であるかどうかは変わらないこともわかります。×がつくかどうかは、その左側に●・■が奇数個あるかどうかのみに依存するので、(3)右側のブロックの×の位置や個数も変わりません。

以上をまとめると、〇を1つ追加したときは(1)(3)に含まれる×の数は変わらず、(2)に含まれる×の数は「2増える」または「1減る」のどちらかであることがわかりました。
つまり、どのように〇を1個追加しても、全体の×の数は「2増える」または「1減る」のいずれかになるということが確かめられました。

したがって、〇を追加していく度に、×の数を3で割った余りは「0→2→1→0→2→1→0→…」と周期的に変化していきます。つまり〇をn-1(=3m+1)個追加すると、×の数を3で割った余りは必ず2になることがわかります（※3）。

アイデアを駆使して、×の数の矛盾を導こう！

先ほどは「どんな方法で〇をn-1(=3m+1)個追加しても、×の数を3で割った余りは2になる」ことを証明しました。つまり「もし〇がn(=3m+2)個並んだとき、×の数を3で割った余りは2にならない」ことを証明できれば、〇がn(=3m+2)個並ばないことが証明できます。

アイデア1のところで説明した通り、「□〇〇…〇〇□」「□〇〇…〇〇■」「■〇〇…〇〇□」「■〇〇…〇〇■」が実現できないことを証明すれば良いです（※4）。これらに×をつけると、以下のようになります。

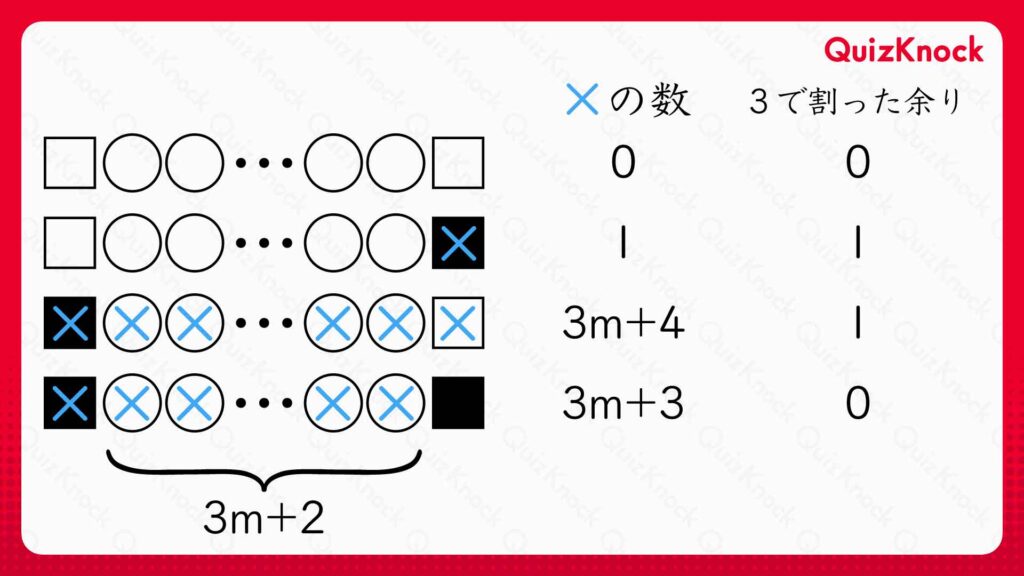
つまり、もし仮に〇をn(=3m+2)個並べることができれば、最終的な×の数を3で割った余りは0か1になります。しかし先ほど「どんな方法で〇をn-1(=3m+1)個追加しても、×の数を3で割ると余りは2になる」ことを証明したため、矛盾します。

したがって、〇をn(=3m+2)個並べることは不可能です。前半の証明と合わせると、「n個の石をすべて〇にすることができる」という条件を満たすnは「3で割った余りが0か1になるようなn」であることがわかります。（証明終わり）

おわりに

無事証明ができたということで、ここまでの流れをおさらいしてみましょう。

上記のステップで、nの条件を求めました。

この問題のポイントは以下の3つです。他の数学の問題を解くときにも、このポイントを意識してみると良いかもしれません。

なお、今回紹介した解答はあくまで一例です。一般的によく知られている解答では、二面体群D₃を用いて証明しています。非常にエレガントな証明で、群について知らなくても行列の積の計算を知っていれば理解できるので、興味のある方はぜひ参考文献をご参照ください。

【あわせて読みたい】

【このライターの他の記事もどうぞ】