伝説の東大数学は算数で解ける【1998年後期】

こんにちは。東大数学科の鹿野です。

今回は、大学入試問題のなかで史上最も難しいといわれている、1998年東京大学後期理系数学第3問（2）について、解説します。

そんな難しい問題、自分には理解できないかも……と心配している方もいるかもしれませんが、ご安心ください。実はこの問題、問題文や解説を理解するだけなら、数学の知識や数式はほとんどいりません。

目次

◎「伝説の東大入試」と呼ばれる理由
◎実際の入試問題を見てみよう
◎何から手をつけたら良いかわからない、そんなときは？
◎「不可能」を証明するには？
◎難しい数学問題を解くコツ

予備校が解けないほど難しい！

さて、実際に出題された問題を見る前に、今回扱う入試問題がどれほど難しいかがわかるエピソードをひとつご紹介します。

この伝説の入試問題に頭を悩ませたのは、受験生だけではありません。毎回、インターネットや新聞で解答速報を公開している予備校も大変な混乱だったそうです。

ある予備校では問題を入手したものの、あまりの難しさに解答作成を中断し、スタッフは帰宅することに。別の予備校でも受験日当日に解けなかったため、大学助教など外部の専門家に協力を求め、受験日から2日後にやっと解答を作り上げたのだとか。

予備校や専門家が知力を結集しても苦戦するレベル。この問題が、いかに難しかったかがわかります。

実際の問題

これが実際の入試問題です。ただし、この後わかりやすく解説しますので、詳しく読まなくても大丈夫です。

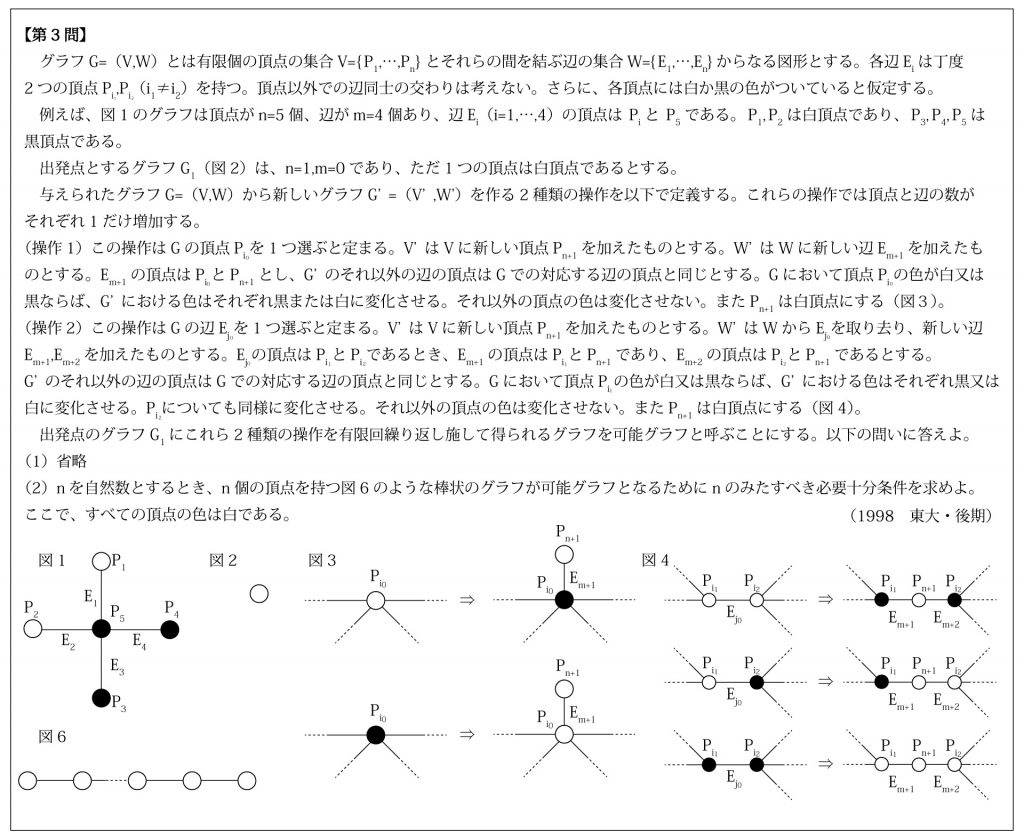
それがこちらです。

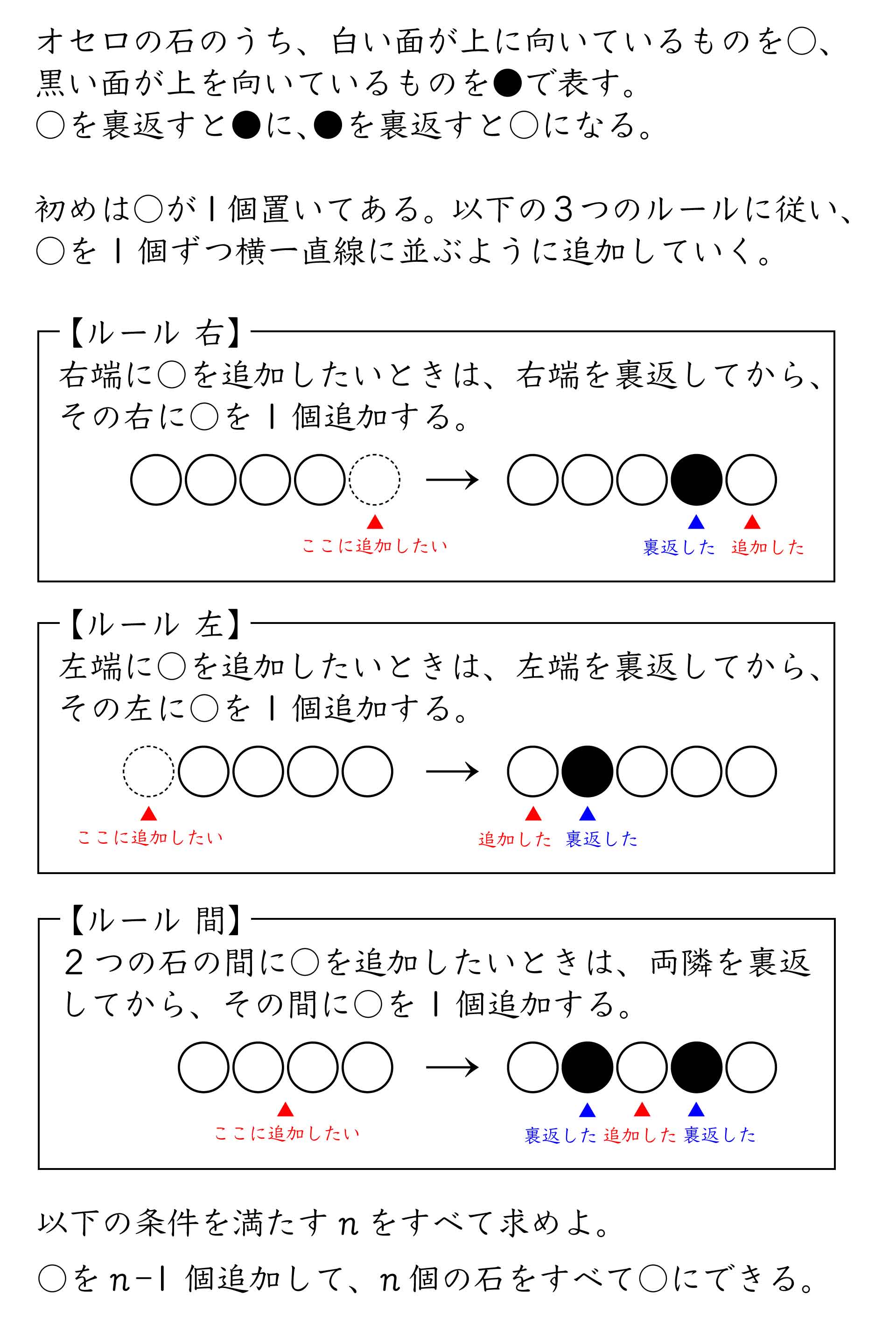
例えば、以下のように〇を5個追加すれば、〇が6個並ぶため、n=6は条件を満たします。

しかし、初期状態から〇を1個だけ追加すると、〇●または●〇となります。〇が2つ並ぶことはありません。つまり、n=2は条件を満たしません。

では、n=100やn=12345などは条件を満たすか？　どんなnが条件を満たすか？　ということを考えるのがこの問題です。

以降は、読みかえた問題文で考えていきます。また、「〇をn-1個追加して、最初にあった石と合わせて〇をn個並べることは可能である」を単に「〇をn個並べられる」などと表します。

実験して答えを予想してみる

そこで、まずはこの問題設定に慣れるためにも、実際に手を動かしてオセロの石を置いてみましょう。

最初に置いてある石は1個の〇のみです。ここに〇を1個追加する方法は2通り（右端/左端に追加）あります。このうち、例えば右端に追加する場合は、ルール右が適用されるため●〇となります。また、この●〇に、さらに〇を1個追加する方法は3通り（右端/真ん中/左端に追加）あります。

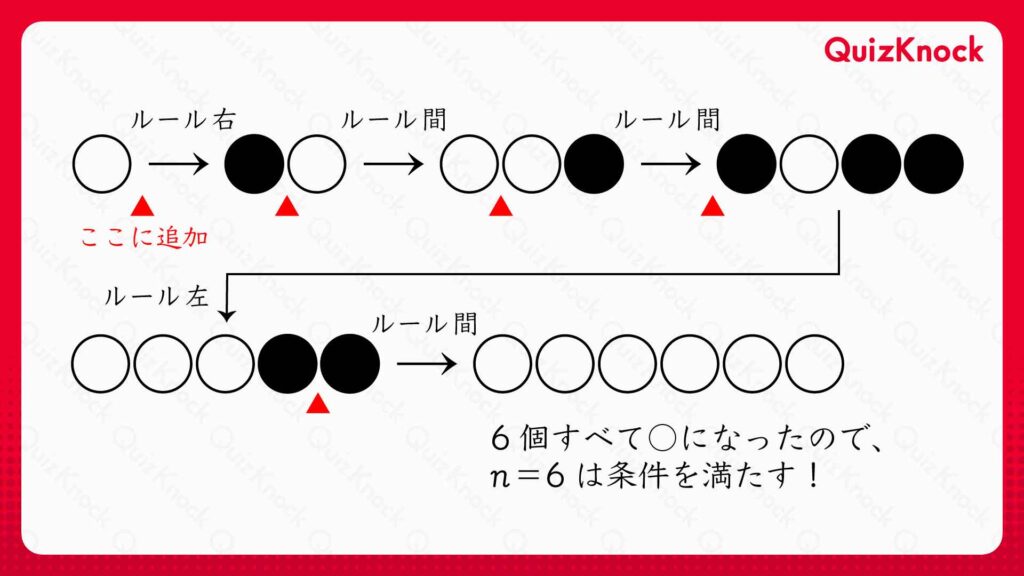
このようにして、最初に置いてある〇に、〇を1個ずつ追加していくと、以下のような表が得られます。

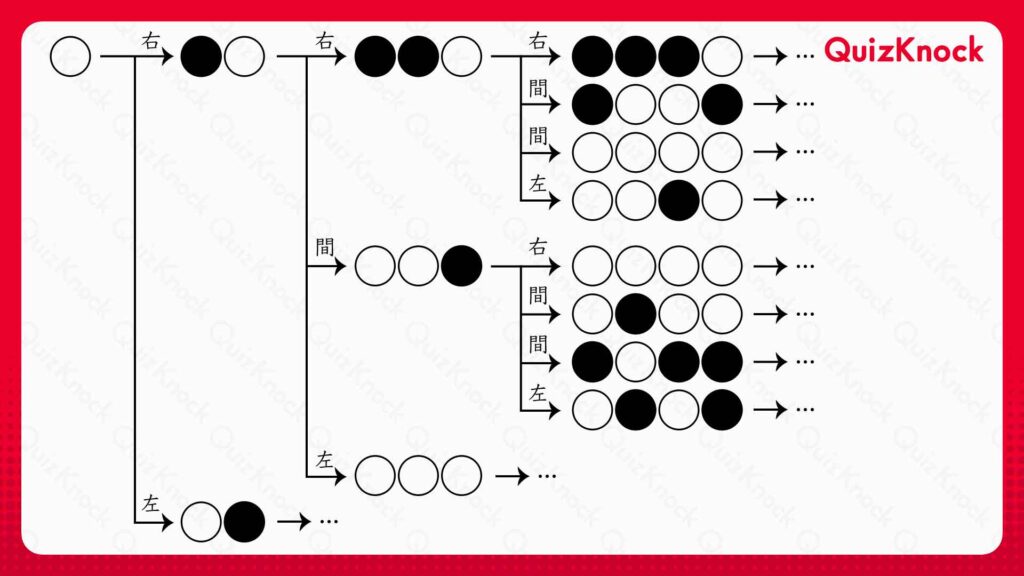
この表から、〇を1,3,4個並べられることがわかります。つまり、n=1,3,4は条件を満たします。一方、先ほど説明したように〇を2個並べることはできないため、n=2は条件を満たしません。

同様にしてすべての追加法を試すことで、n=5は条件を満たさず、n=6は条件を満たすことがわかります。 n=1,3,4,6は条件を満たし、n=2,5は条件を満たさないので、nを3で割ったときの余りが0,1のときは条件を満たし、余りが2のときは条件を満たさないと予想できます。これを証明すれば良さそうです。

まずは「可能」であることを証明しよう！

まずは、nを3で割った余りが0,1のときに条件を満たすことを証明します。つまり、〇を1,4,7,……個および3,6,9,……個並べられることを証明します。

先ほどの表をもう一度見てみましょう。

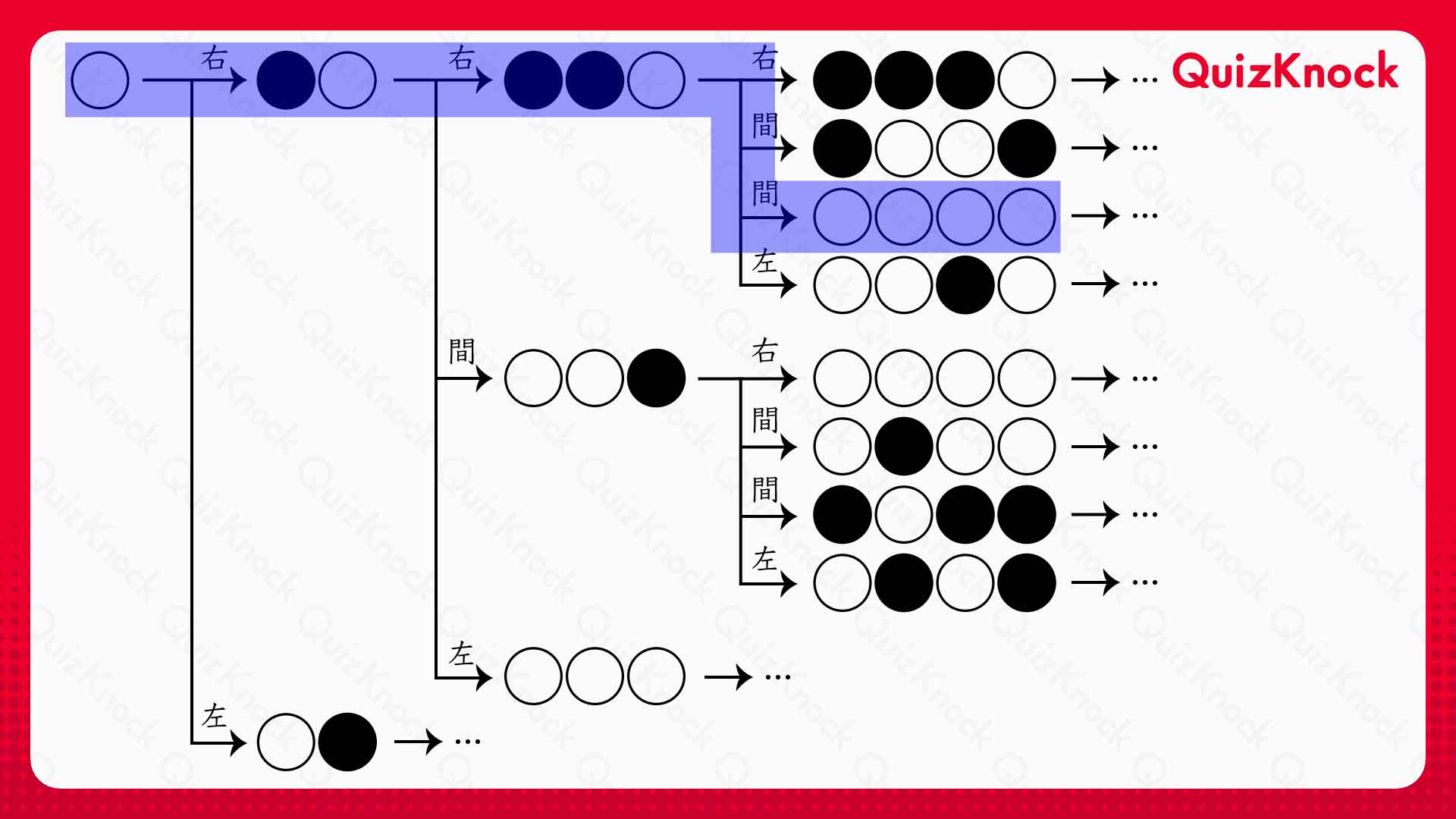
青枠で囲まれた部分に注目します。〇を「右端→右端→右から2,3番目の石の間」の順に3回追加することで、〇を4つ並べることができています。

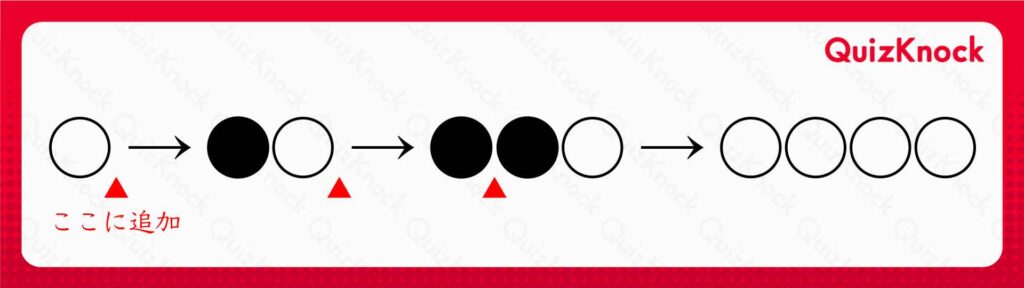
同様にして、さらに〇を3回追加することで、〇を7つ並べることができます。

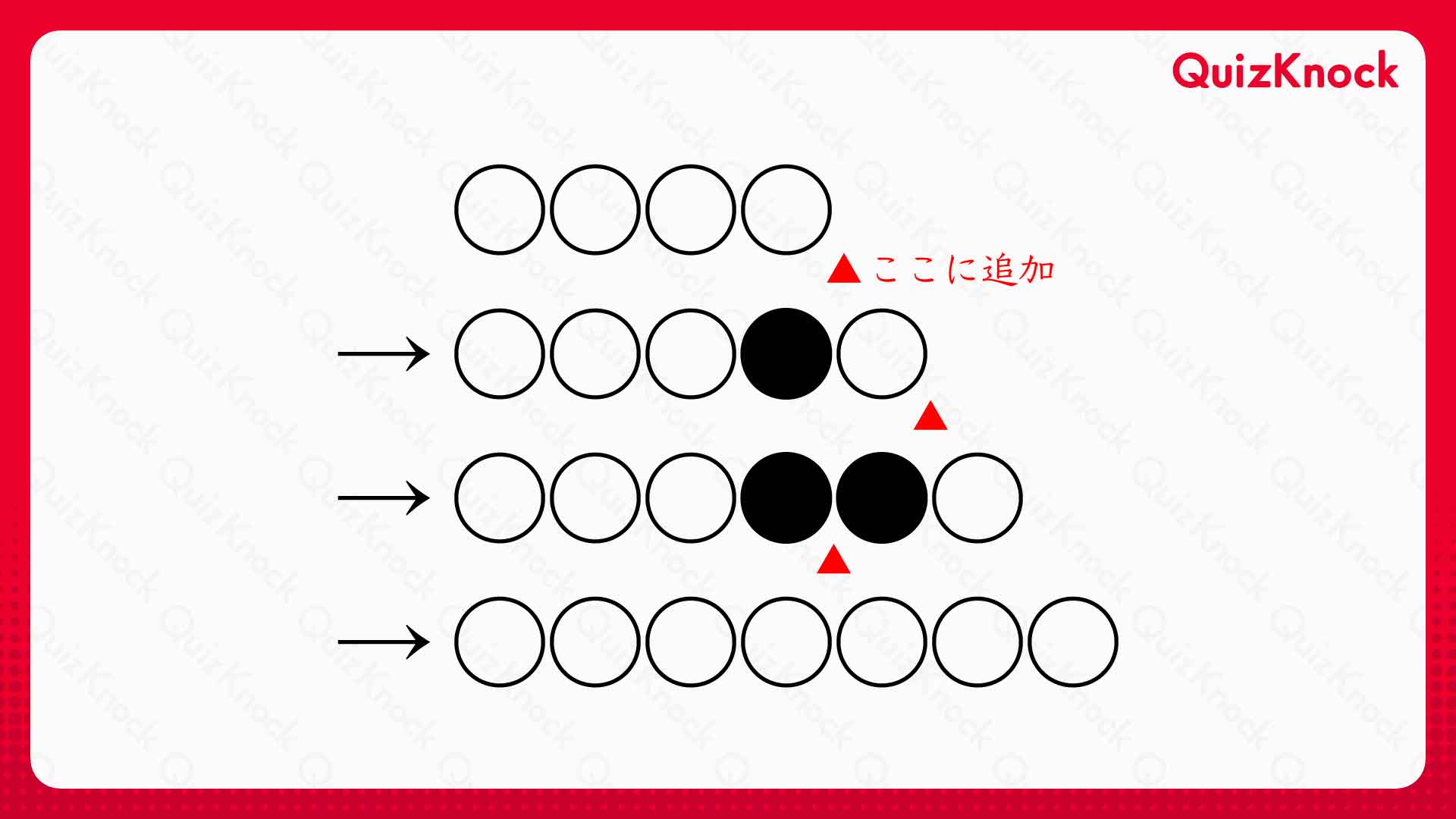
このように「右端→右端→右から2,3番目の石の間」という追加法を繰り返すことで、〇を1,4,7,……個並べることができます。

また、〇を3個並べられることは既に証明したため、同様にして〇を3,6,9,……個並べることも可能だとわかります。

したがって、nを3で割った余りが0,1のときは条件を満たすことが証明されました。

次ページ：ここからが山場！　「不可能を証明」……カギとなるアイデアとは？