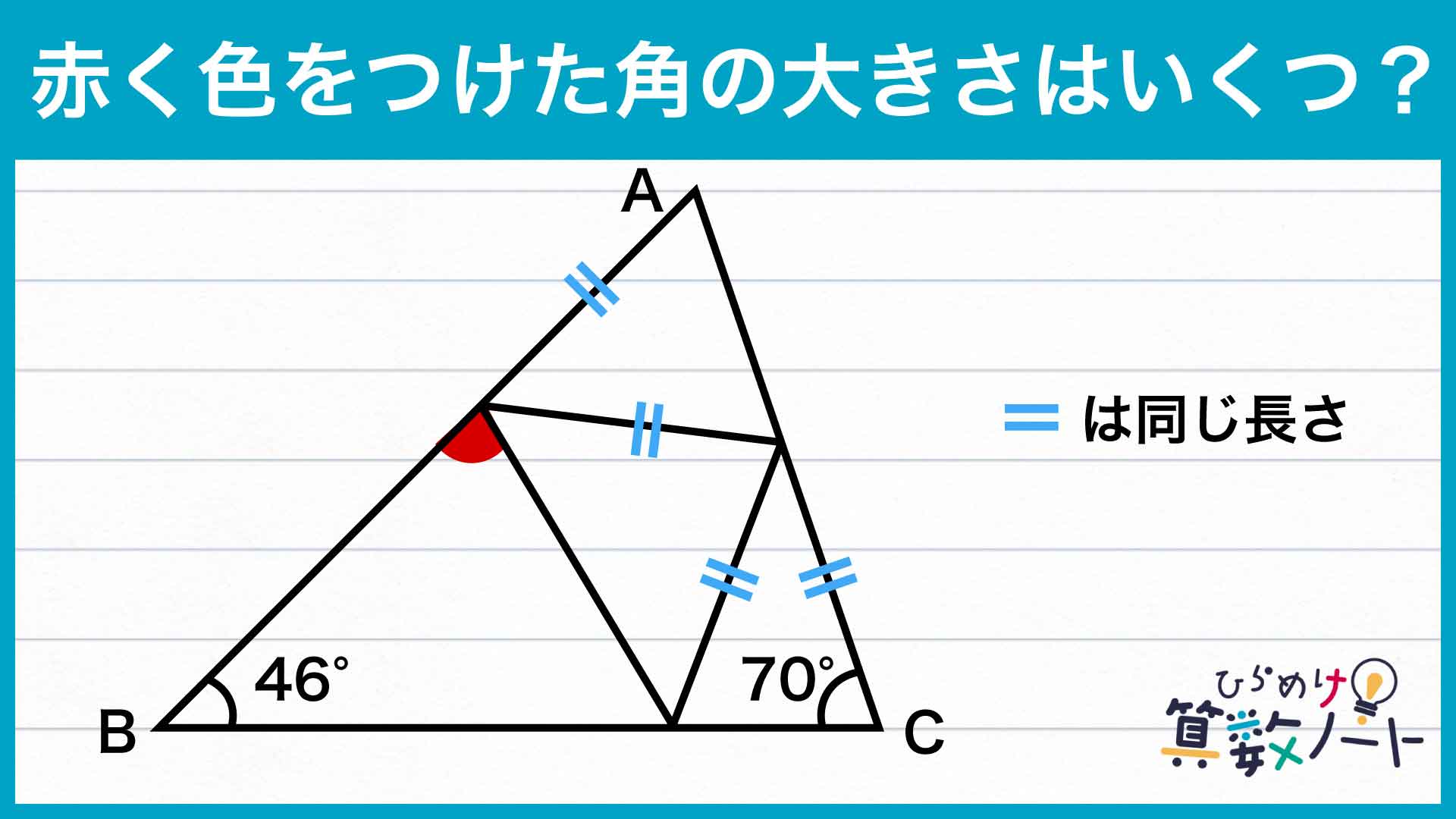
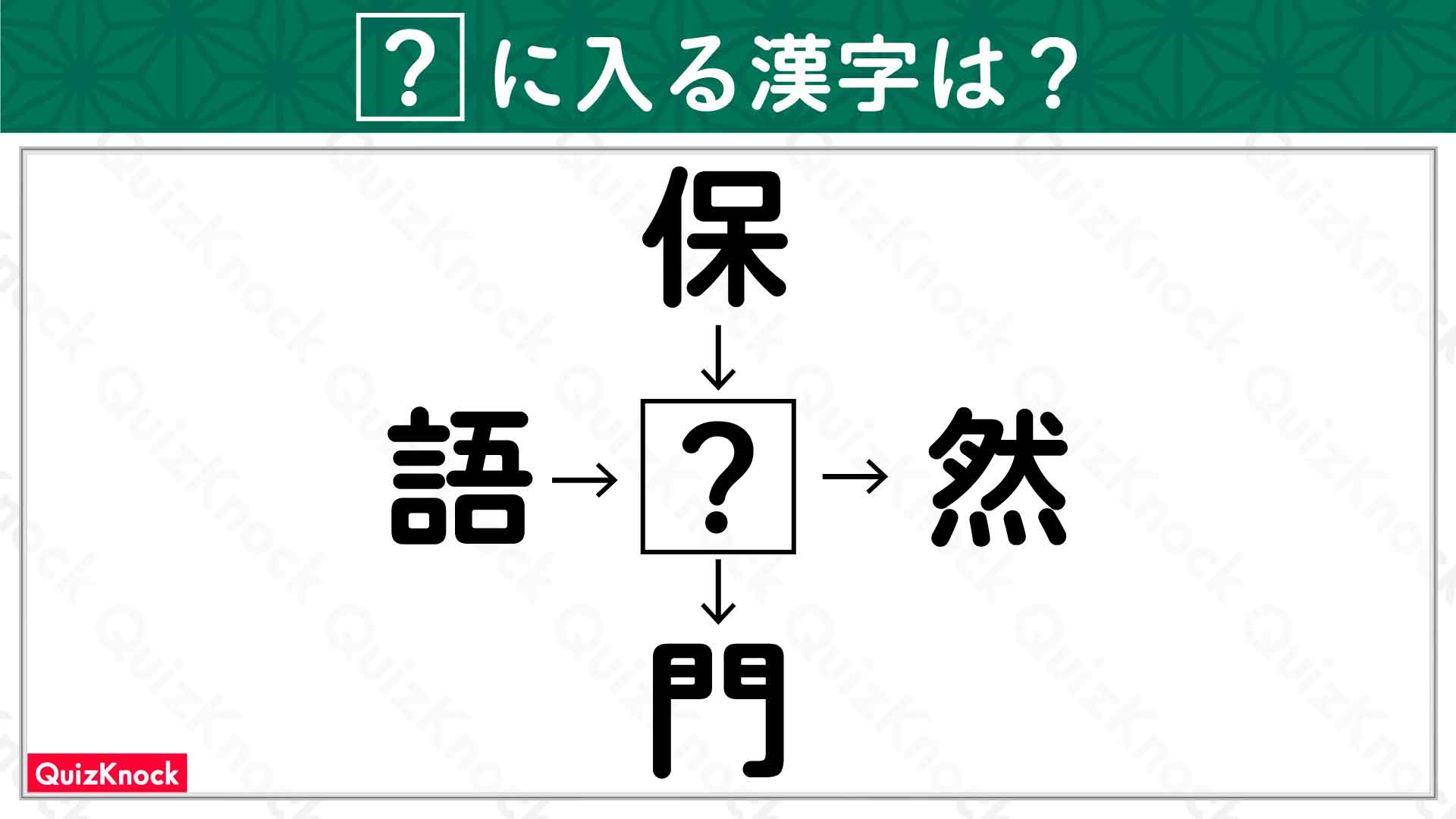
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。ちなみに次のページでは瞬殺で解ける解法も紹介しています。
今回も僕と一緒に解いていきましょう! この算数のシリーズも12回目ということで、僕には赤色の三角形が、滑り台で楽しそうに遊んでいるように見えてきました。みなさんにはどう見えますか?
この問題を解く上で大事なのが、「図形の分割」と「面積の引き算」です。
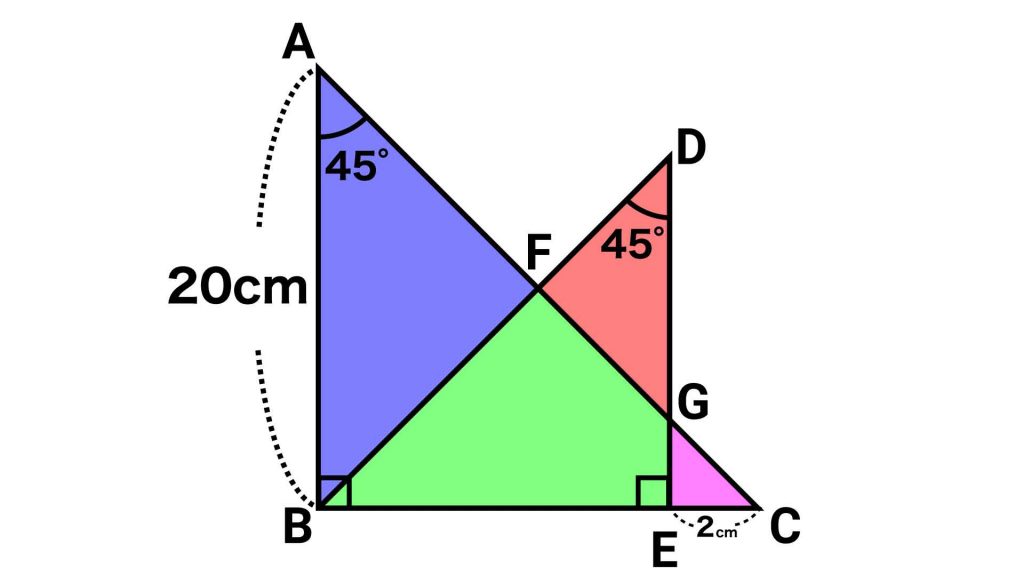
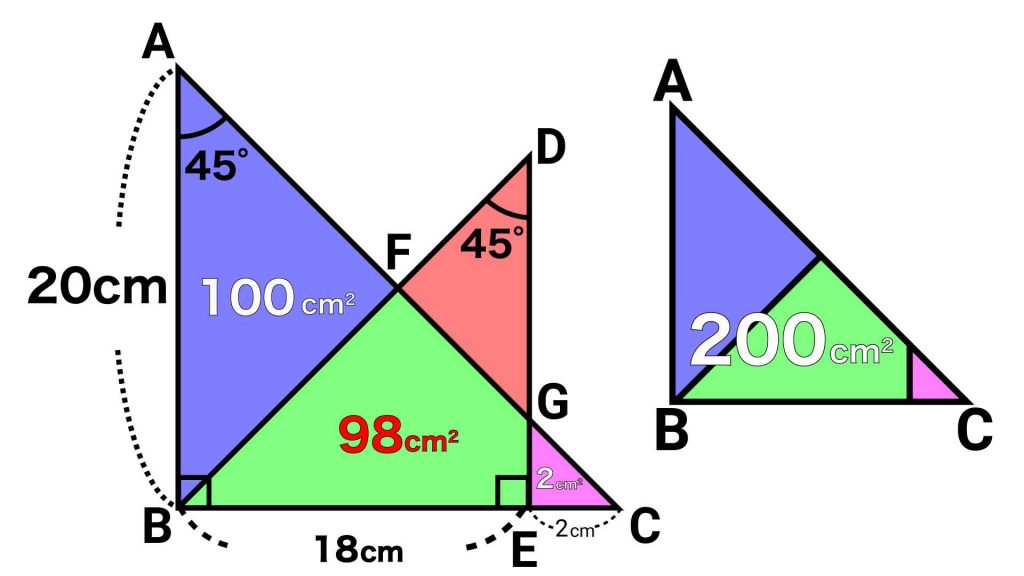
問題の図形を、下の図のように4つの図形に分割します。
三角形DEBに着目すると、三角形DFGの面積は以下のような引き算で求めることができます。
ここで知りたいのが、緑色の図形の面積ですよね。この図形の面積は、以下のように三角形ABCから求めることができます。
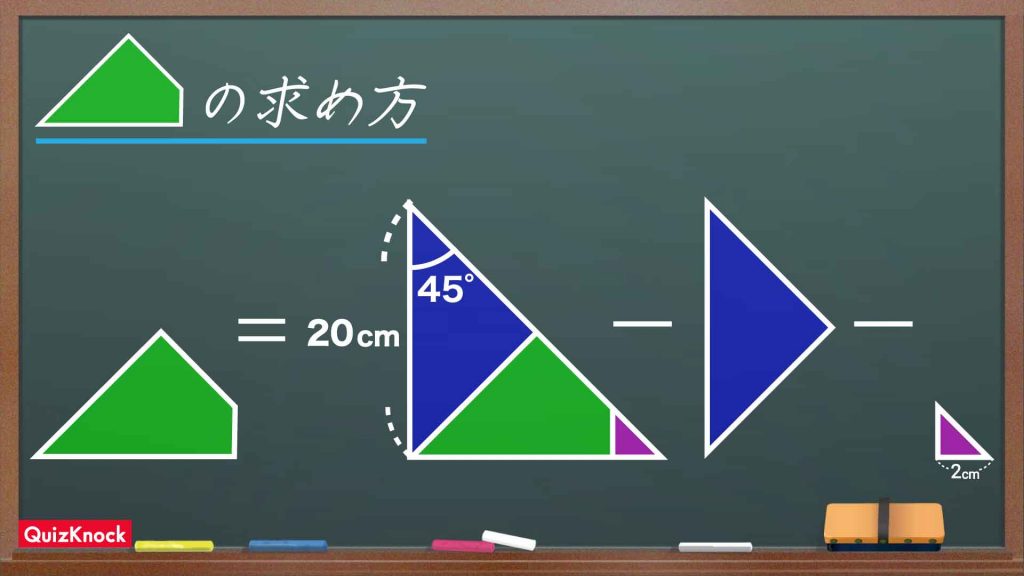
この手順に沿って、解説していきます!
事前準備:面積を求めるのに必要な長さを出す
実際に問題を解く前に、各図形の面積を求めるのに必要な長さを出します。
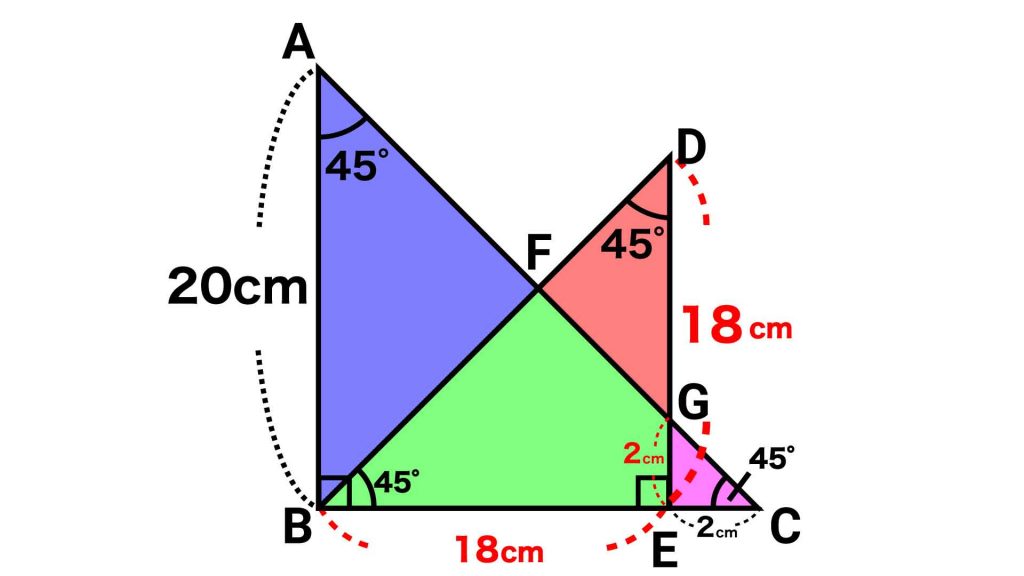
上の図の赤字で示した長さが、面積を求めるのに必要な長さです。
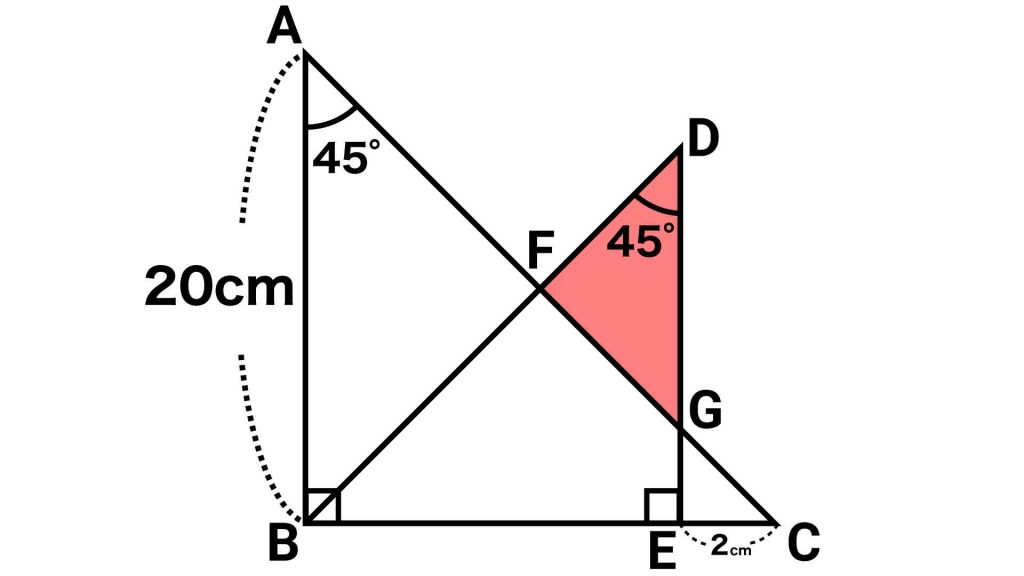
三角形ABCはAB=BCの直角二等辺三角形なので、AB=BC=20cmです。EC=2cmであることから、BE=18cmだとわかります。
また、三角形DEBとGECも、2つの角がそれぞれ45度の直角二等辺三角形なので、DE=EB=18cm、GE=EC=2cmです。
これで準備万端!
緑色の図形の面積を求めよう!
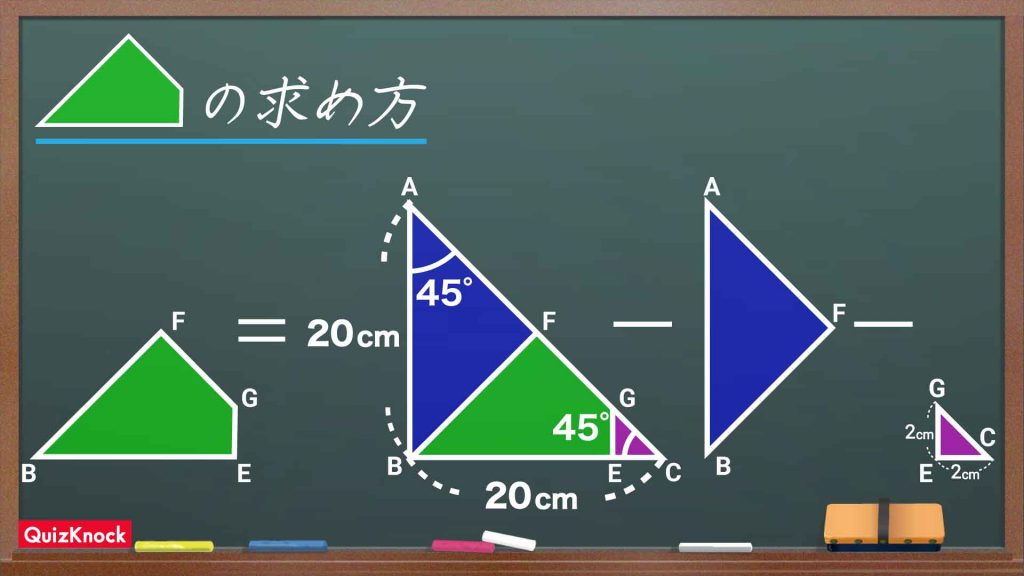
まずは、下の図の引き算を行い、緑色の図形の面積を求めます。
青色の三角形の面積をどう求めるかがポイントです!
まずは一番大きな直角二等辺三角形ABCの面積を求めましょう。1辺が20cmなので、(20×20)÷2=200cm2です。
次に青色の三角形AFBをよく見ると、2つの角がそれぞれ45度の直角二等辺三角形であることがわかります。線分BDが三角形ABCの辺ACと直角で交わっている、つまり辺ACの中点で交わっているため、三角形AFBの面積は三角形ABCの面積のちょうど半分です。
したがって青色の三角形ABFの面積は、200÷2=100cm2です。
また、一番小さなピンク色の三角形GECの面積は、(2×2)÷2=2cm2です。
以上より、緑色の図形の面積は、200-100-2=98cm2となります。
不思議な形の図形でも、ちゃんと面積が求められました!
赤い三角形の面積を求めよう!
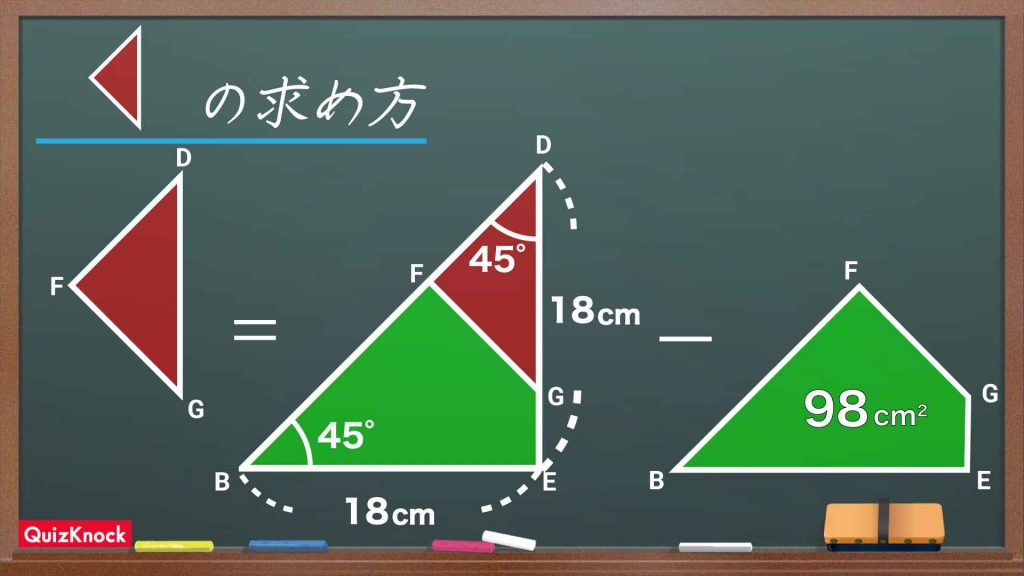
次に、下の図の引き算を行い、赤色の三角形DFGの面積を求めます。
直角二等辺三角形DBEの面積は、(18×18)÷2=162cm2です。
緑色の図形の面積は98cm2なので、赤色の三角形DFGの面積は、162-98=64cm2となります。
答え:64cm2
面積の引き算で答えを求められることに気づけるかがポイントでした。
これで終わりかと思いきや……。








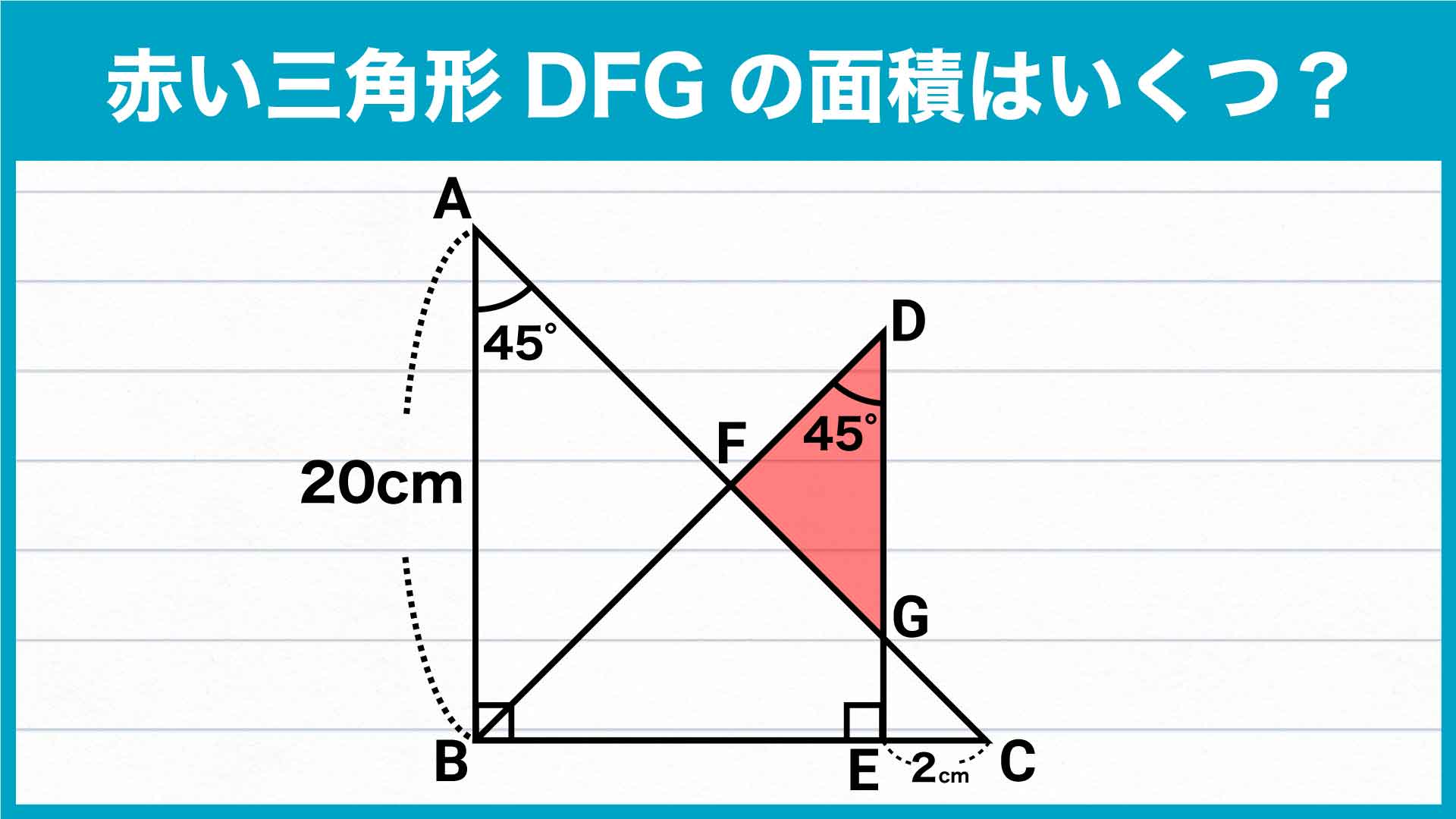










.jpg)