小学5年生で解ける「正方形の面積」を求める問題、あなたは解ける？

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

1ページ：【解答フォーム】自力で解きたい方はこちらへ！　以下は問題の答えです

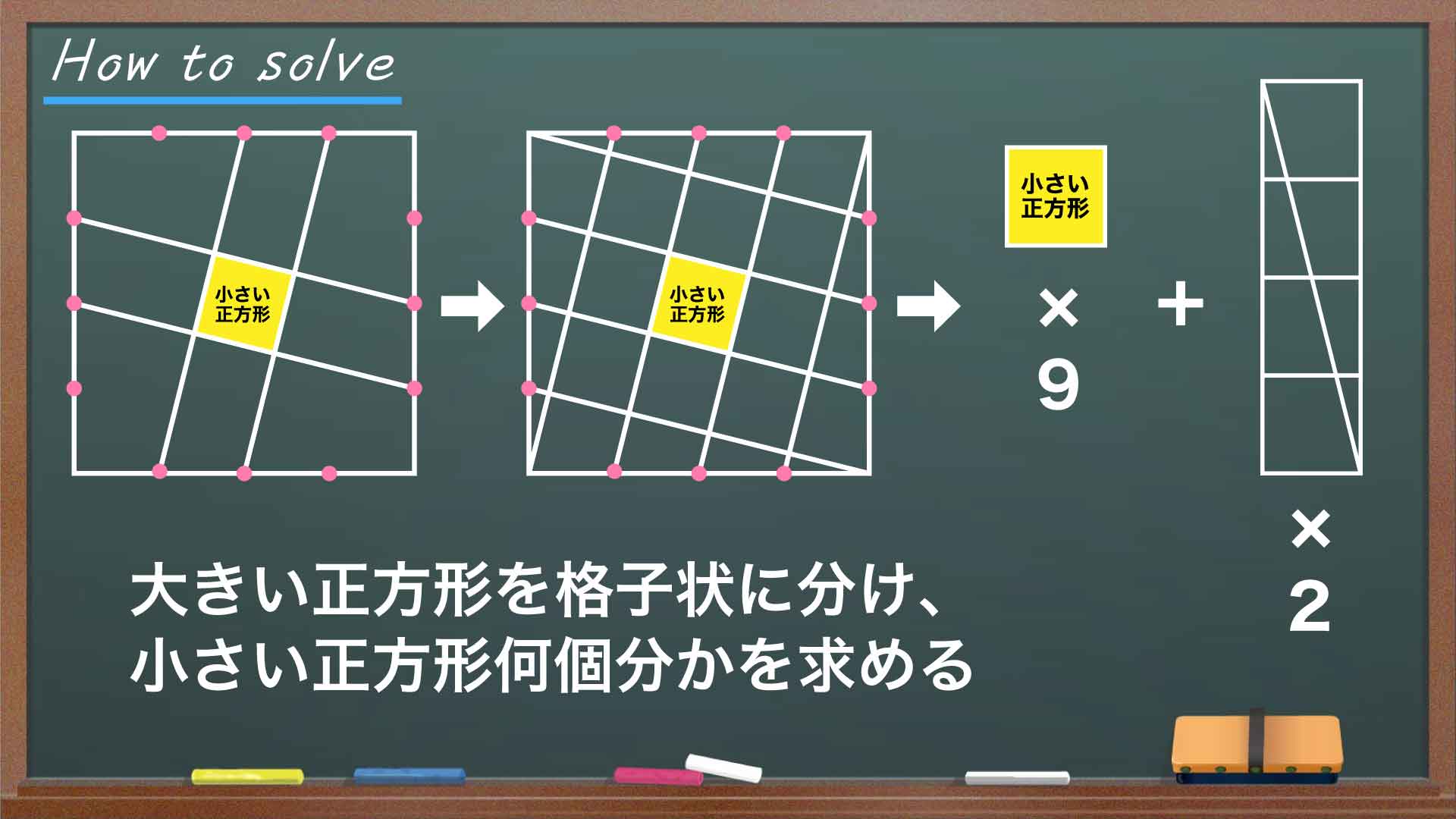
問題の解き方をまとめた図がこちらです。

ポイントは、大きい正方形を細かく分けた上で図形をうまく組み合わせ、小さい正方形何個分かを考えることです。

では、このポイントを踏まえつつ解いていきましょう！

正方形を分割する

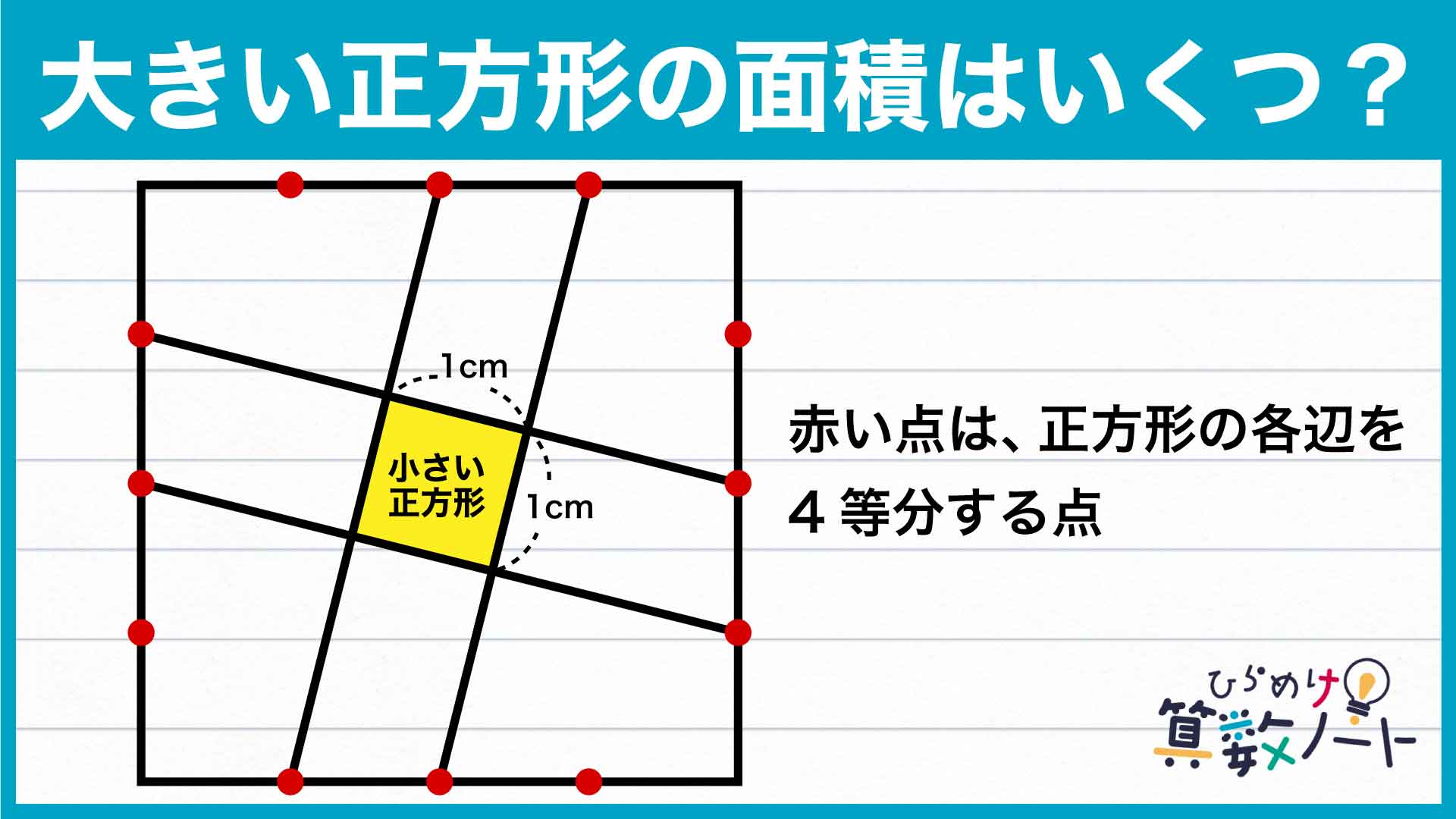
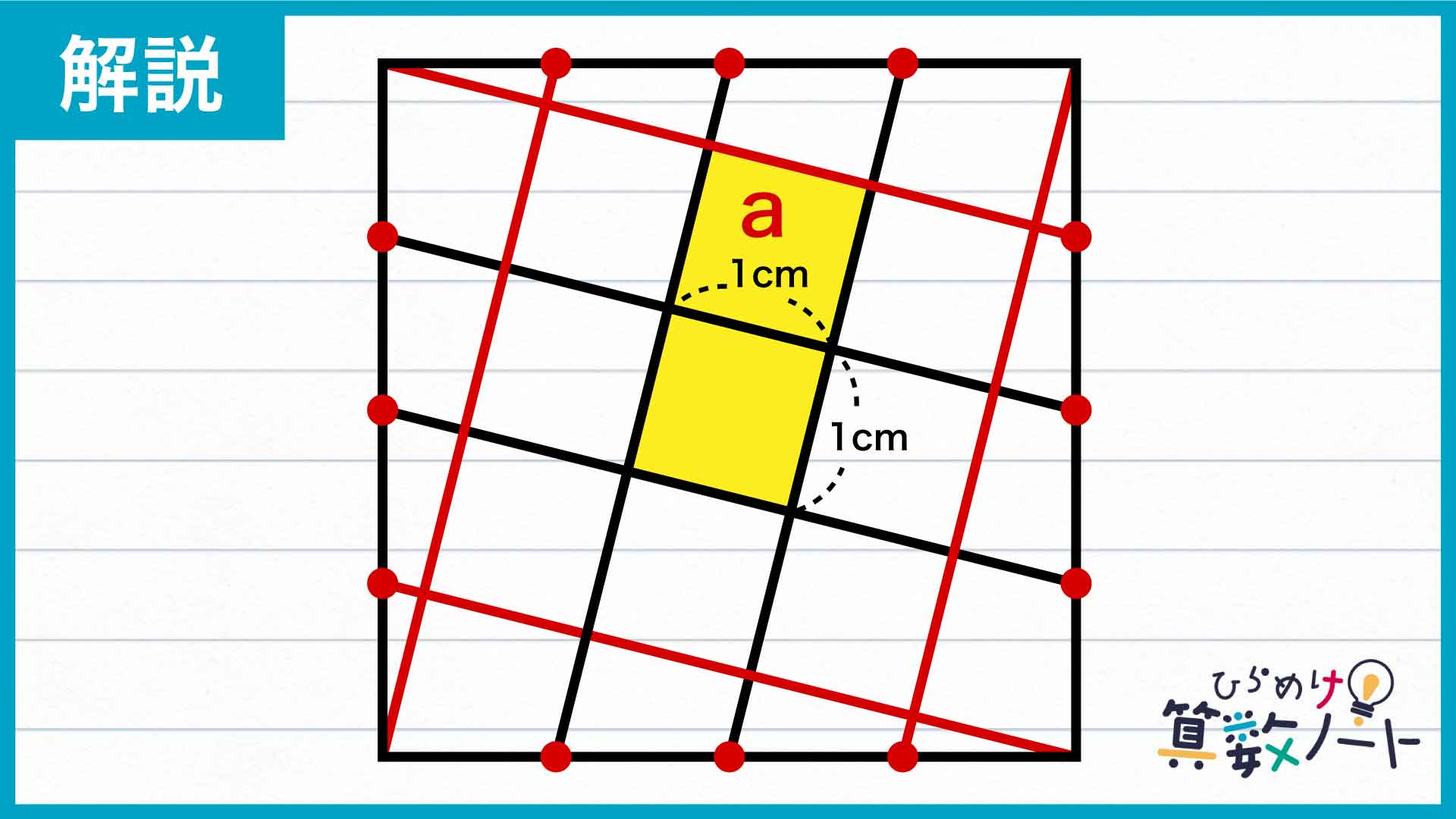
問題画像のような状態では、大きい正方形の辺の長さや面積はわかりません。そこで、大きい正方形の辺を4等分する点および頂点のうち、まだ線で結ばれていないものを同様に繋いでみます。

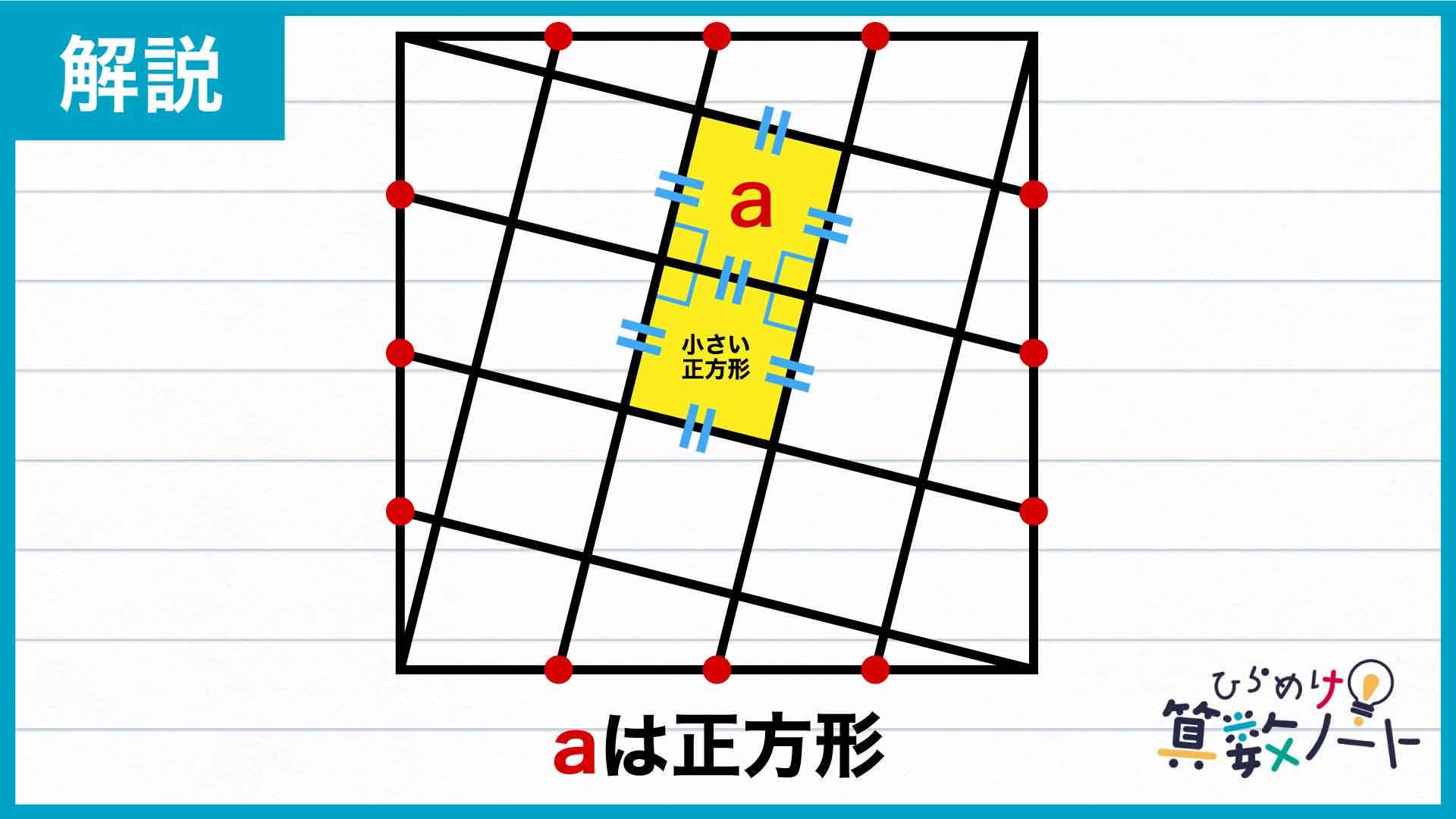
中央部にできた格子模様のうちaの部分に着目し、小さい正方形と比べてみます。大きい正方形は平行な線分で区切られていることからaは平行四辺形であり、また線分はいずれも等間隔で引かれていることから、aの各辺の長さは小さい正方形の1辺と等しくなっています。また、正方形の角と隣り合う角の大きさは180-90=90度であり、aが持つ2つの角が直角であることから、この図形もまた正方形であることがわかります。

同様にして、中央部分には小さい正方形と合同な図形が9つあることがわかるのです。

周囲部分の面積を求める

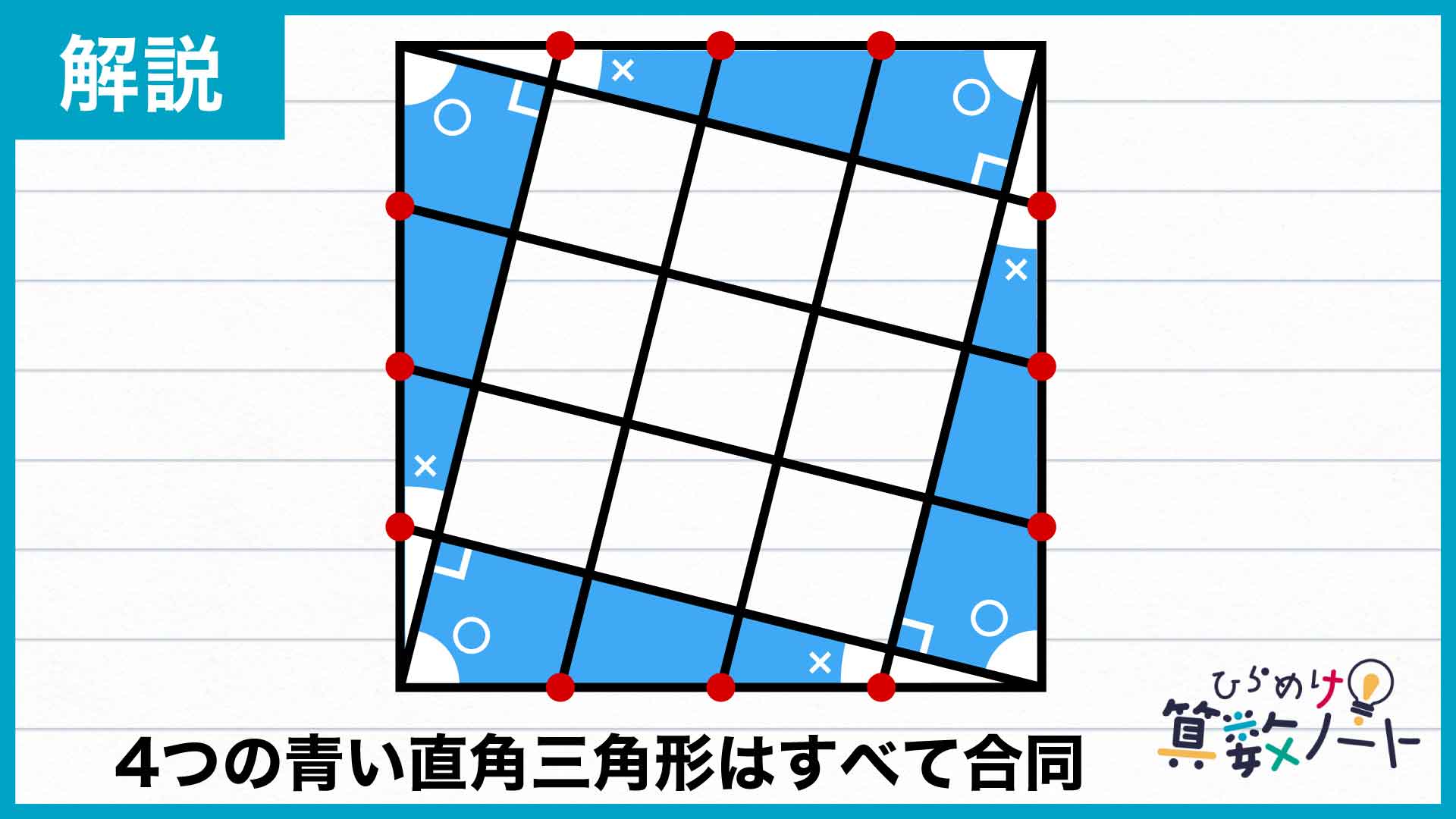
周りの部分は、下図のようにして4つの青い直角三角形に分けることができます。bの三角形が持つ内角のうち、直角でない2つを〇、×とすると、〇+×=90度が成り立ちます。

したがって、隣の直角三角形の内角についても大きさがそれぞれ90-〇=×、90-×=〇であるとわかり、同様の計算を繰り返すとそれぞれの角の大きさは以下のようになります。さらに、斜辺の長さはそれぞれ大きい正方形の1辺と等しいことから、これら4つの直角三角形は合同です。

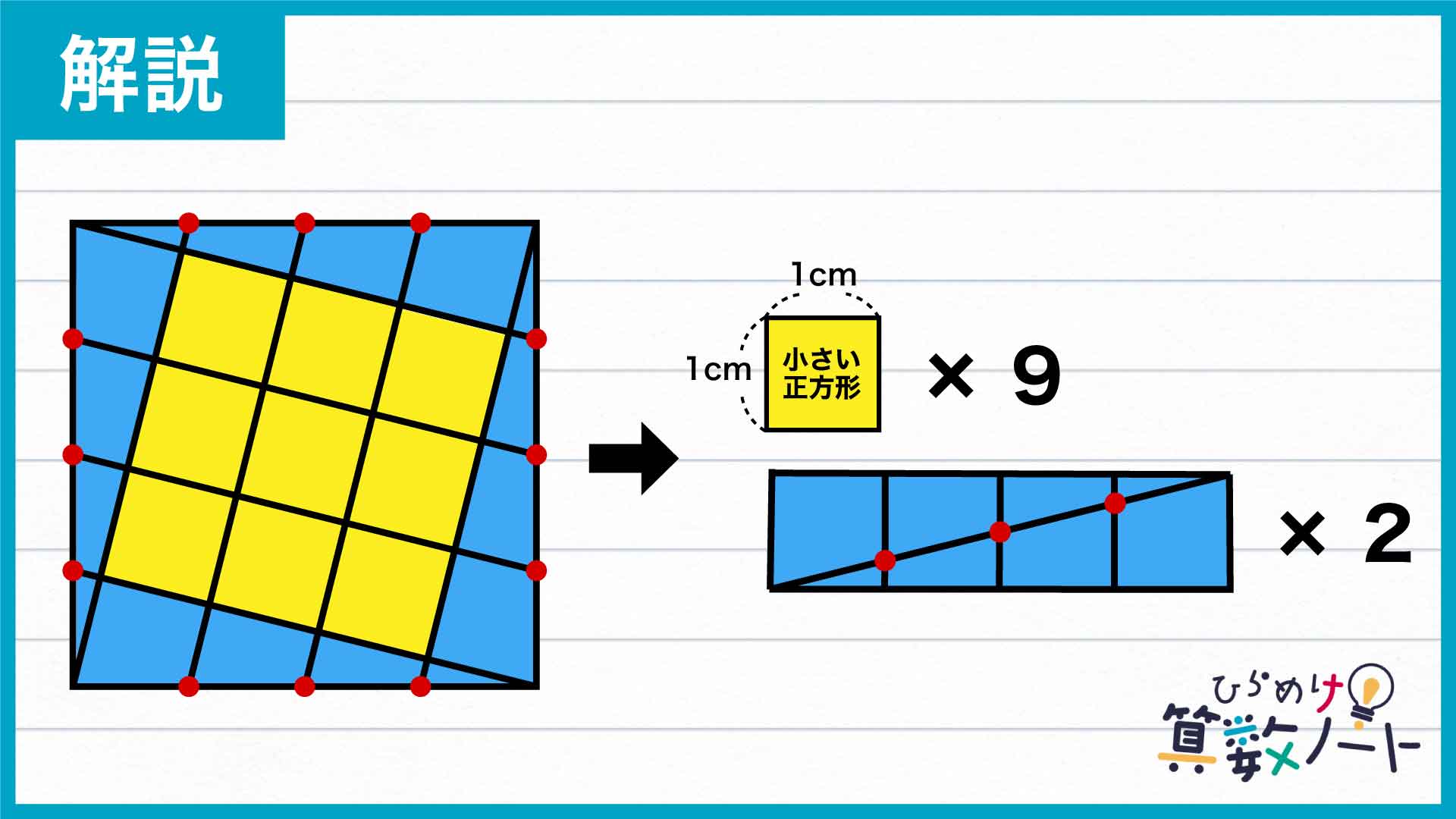
そして、この直角三角形2つを組み合わせてみると、1つの長方形が完成します。この長方形は、小さな正方形4つを繋げてできていることがわかります。

各部分の面積を足す

あとは、求めた各部分の面積を足し合わせて大きい正方形の面積を求めます。中央部分は小さい正方形9つ分、周辺部分は小さい正方形4×2=8つ分の面積を持つので、大きい正方形の面積は小さい正方形の面積の9+8=17個分であることがわかります。

小さい正方形の面積は1×1=1cm²なので、求める面積は1×17=17cm²となります。

答え：17cm²

「ひらめけ！算数ノート」のバックナンバーはこちら！

【前回の算数ノートはこちら】

【あわせて読みたい】