解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
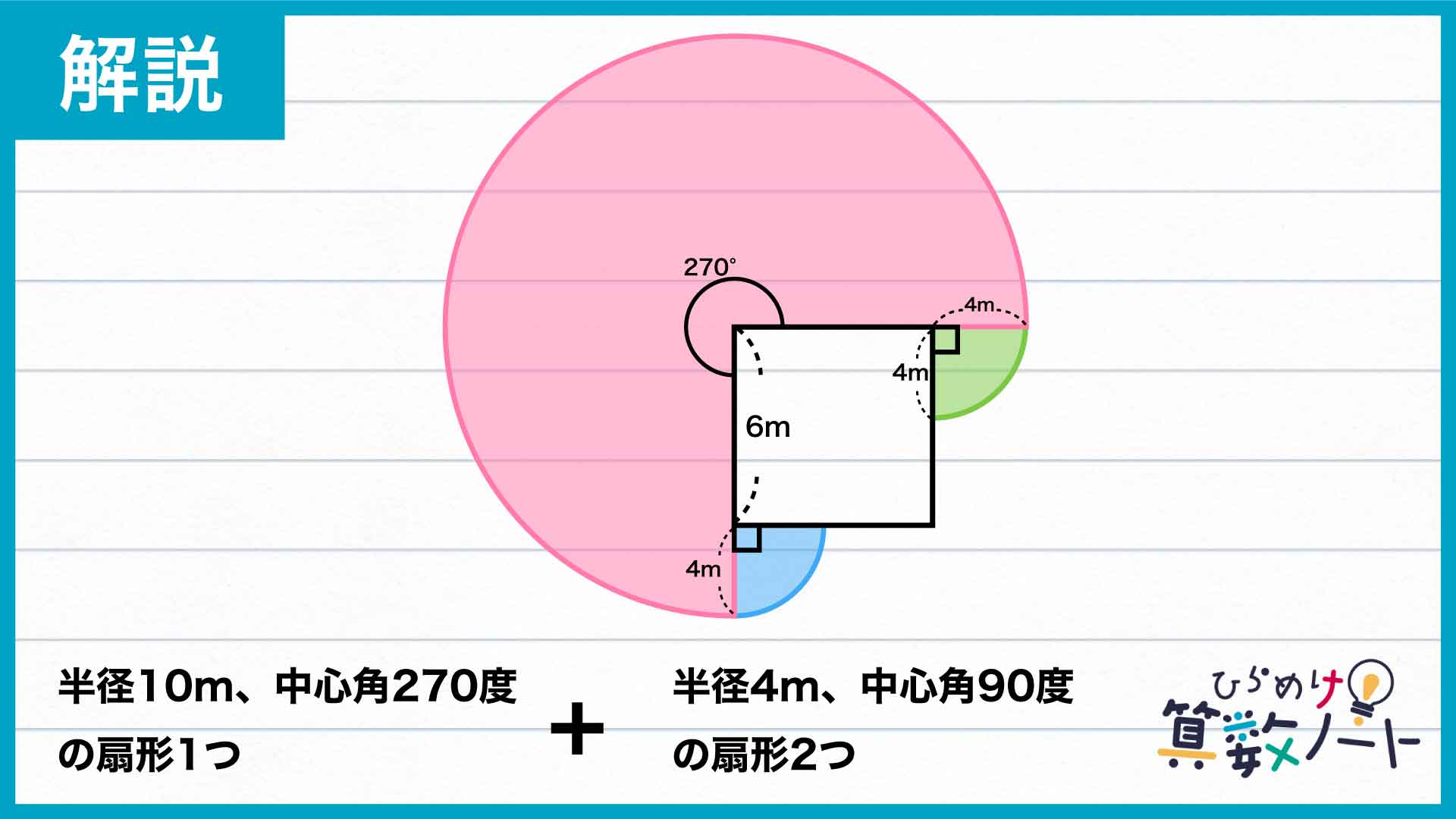
問題の解き方をまとめた図がこちらです。
ポイントは、犬が動ける範囲を複数の扇形で表すことです。
では、このポイントを踏まえつつ解いていきましょう!
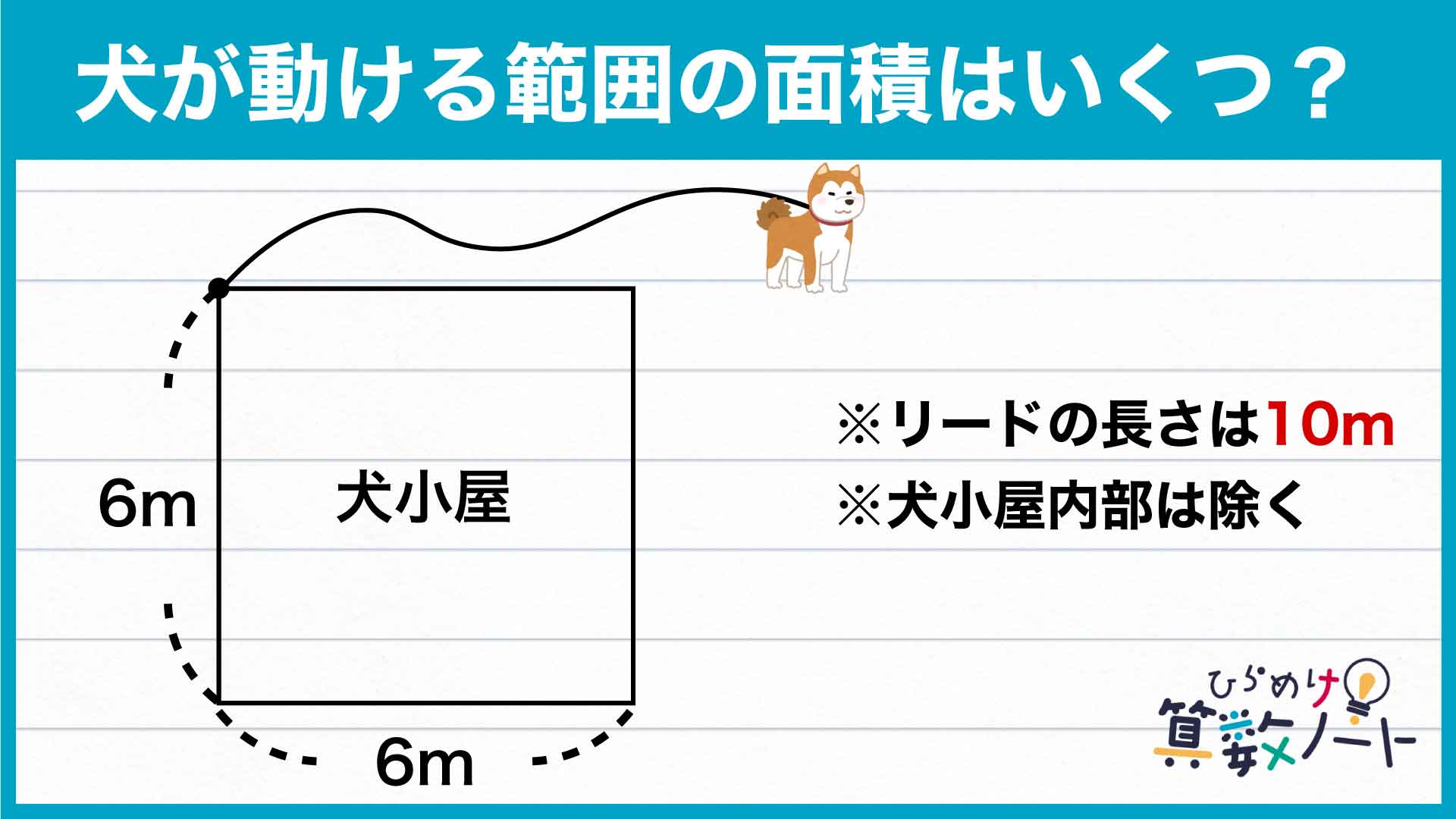
「犬が動ける範囲」はどんな形?
まずは、犬を実際に動かしてみて、動ける範囲を図に表しましょう。リードを目一杯伸ばした状態から、犬が反時計回りに動くとします。このとき、半径10m、中心角90度の扇形の弧を描いたところで、リードが壁に当たってしまうのがわかります。
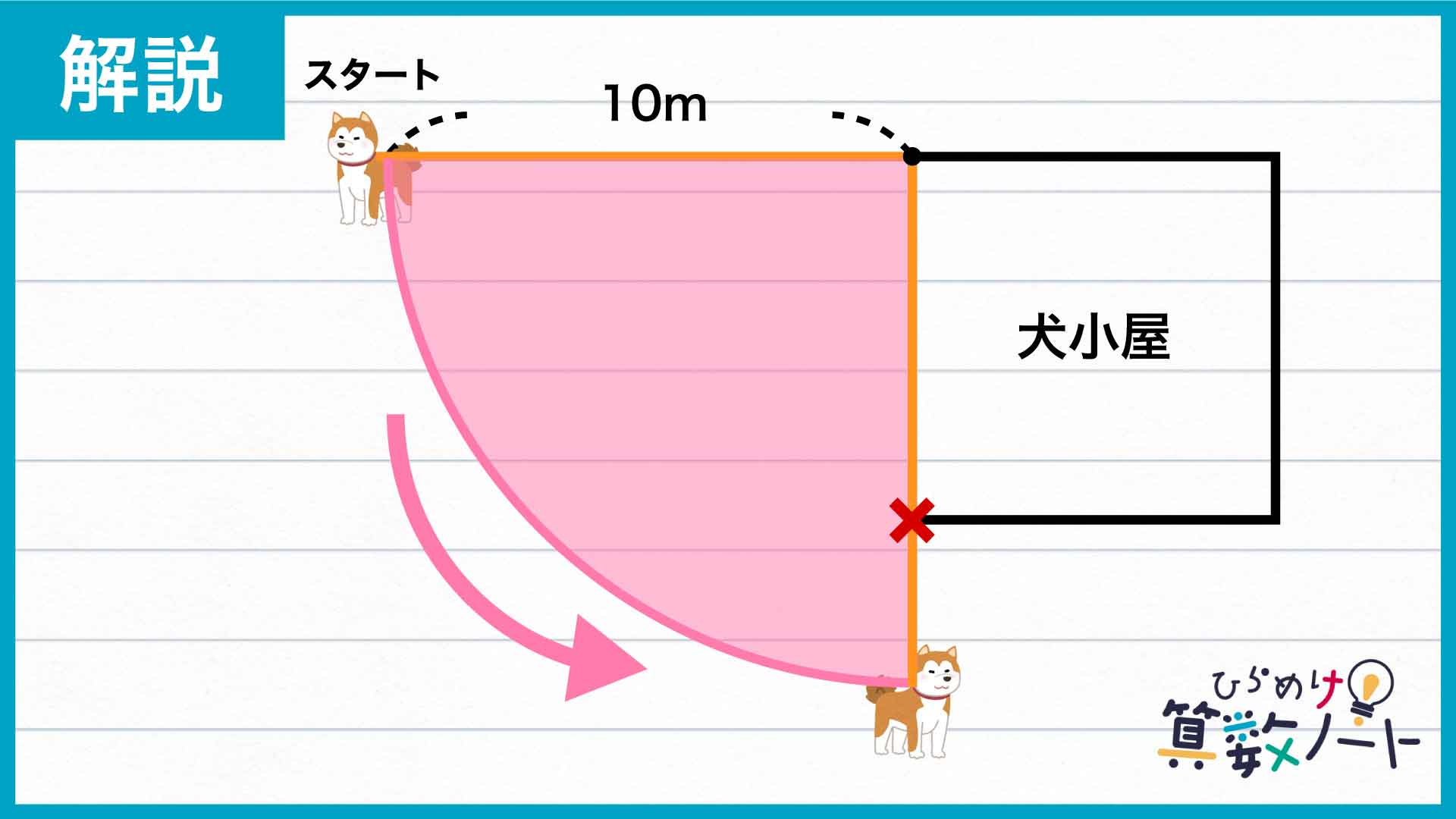
壁に邪魔されたあとの犬の動きを考えてみましょう。犬小屋の左下の角に注目すると、犬のリードが下向きに10-6=4mはみ出ています。犬がそのまま反時計回りに回ろうとすると、今度は左下の角を中心として半径4mの扇形の弧を描くことになるのです。そして、犬が90度回ったところで壁にぶつかり、これ以上は動くことができません。
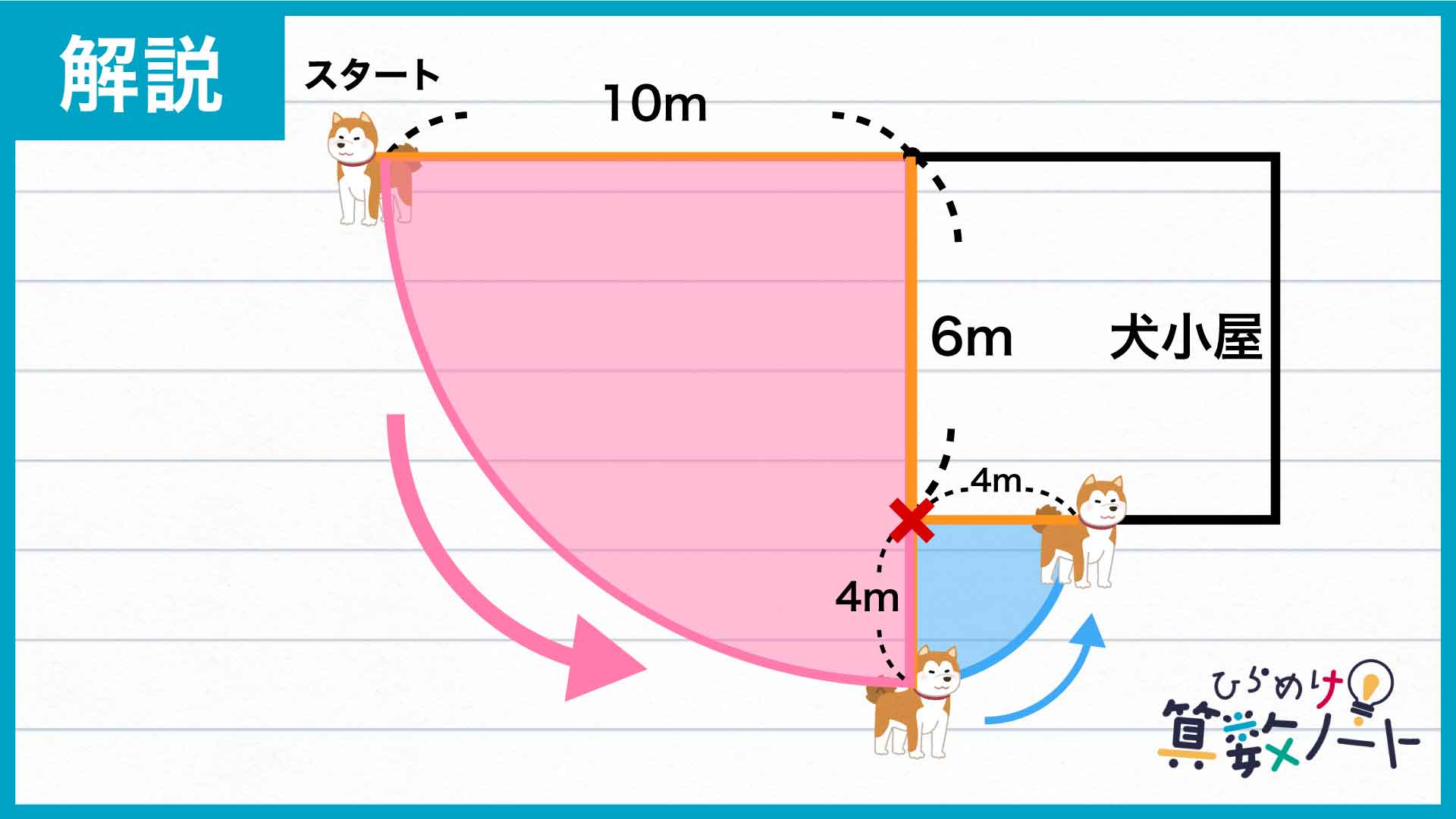
同じようにして、犬が時計回りに動ける範囲を考えます。半径10mの半円の弧を描いたところで壁にリードが当たり、その後はやはり半径4mの扇形の弧を描くように動きます。
扇形の面積を求める
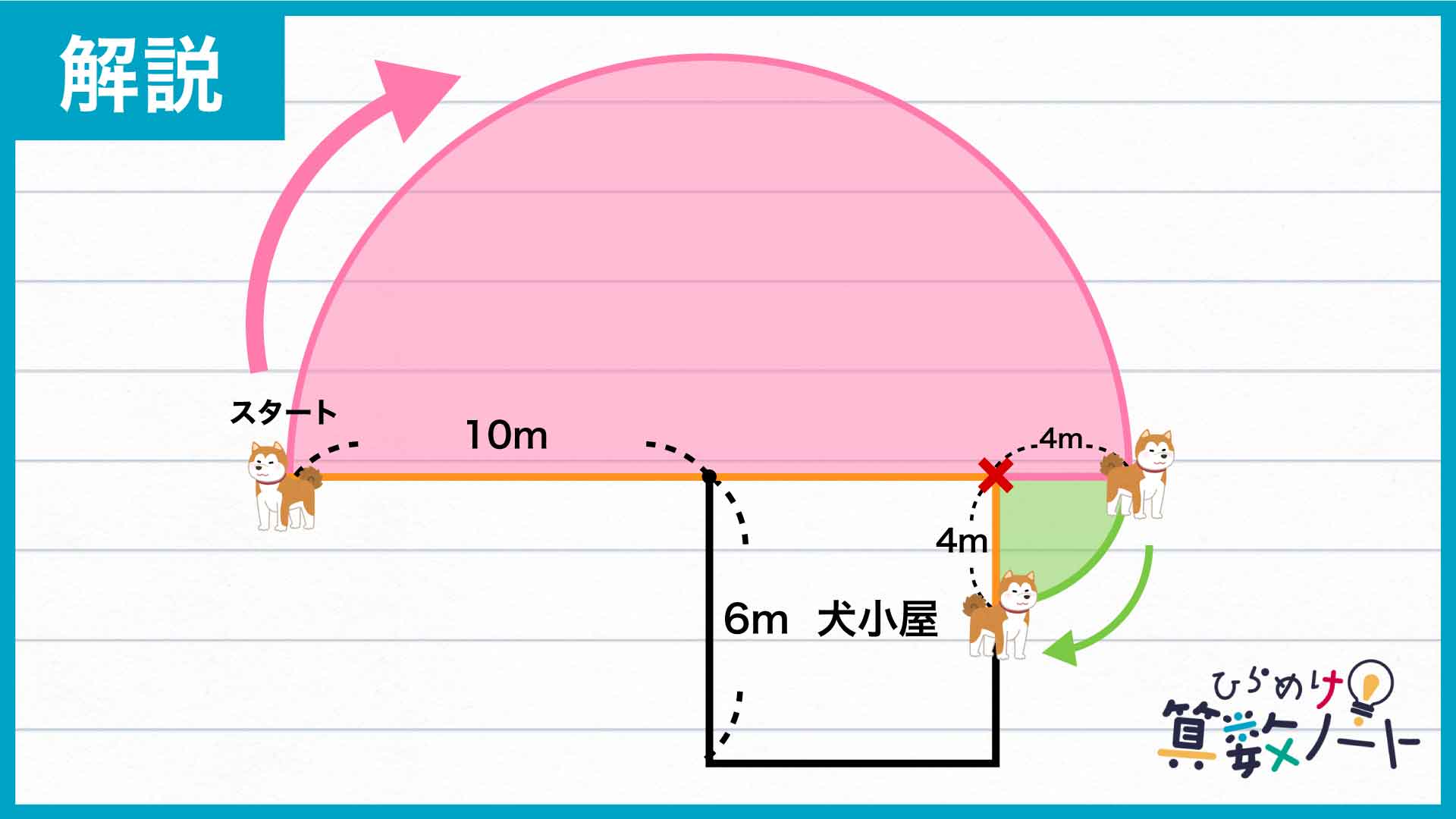
以上のことから、犬が動ける範囲は図のように表せることがわかります。
つまり、求める面積は半径10m・中心角270度の扇形と、半径4m・中心角90度の扇形2個の面積の合計です。
したがってその値は、10×10×π×(270/360)=75π㎡と4×4×π×(90/360)×2=8π㎡を合わせて、75π+8π=83π㎡となります。
答え:83π㎡
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】













.jpg)









.jpg)






