小学6年生で解ける「正八角形の中にある台形の面積」の問題に挑戦！

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

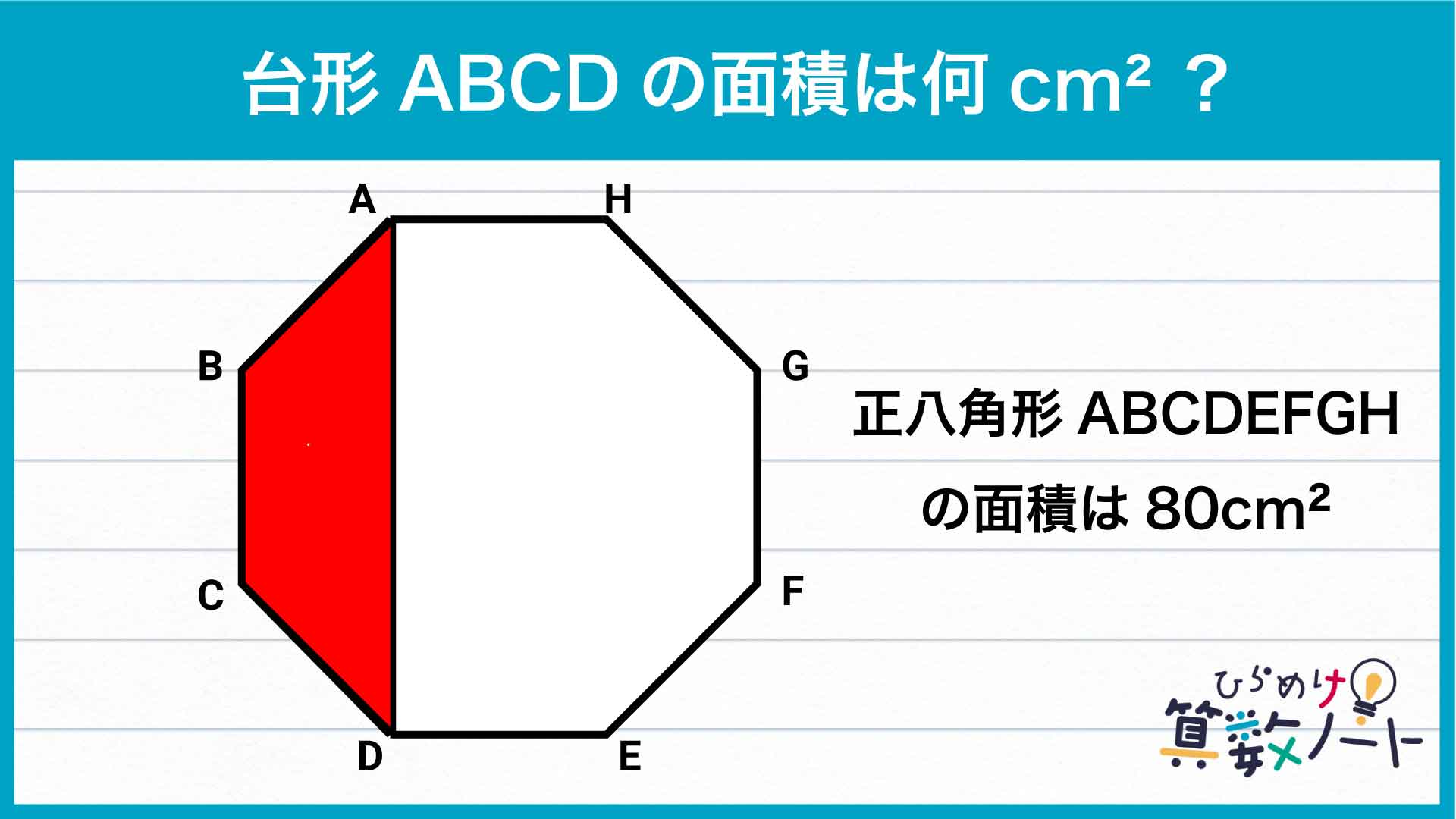
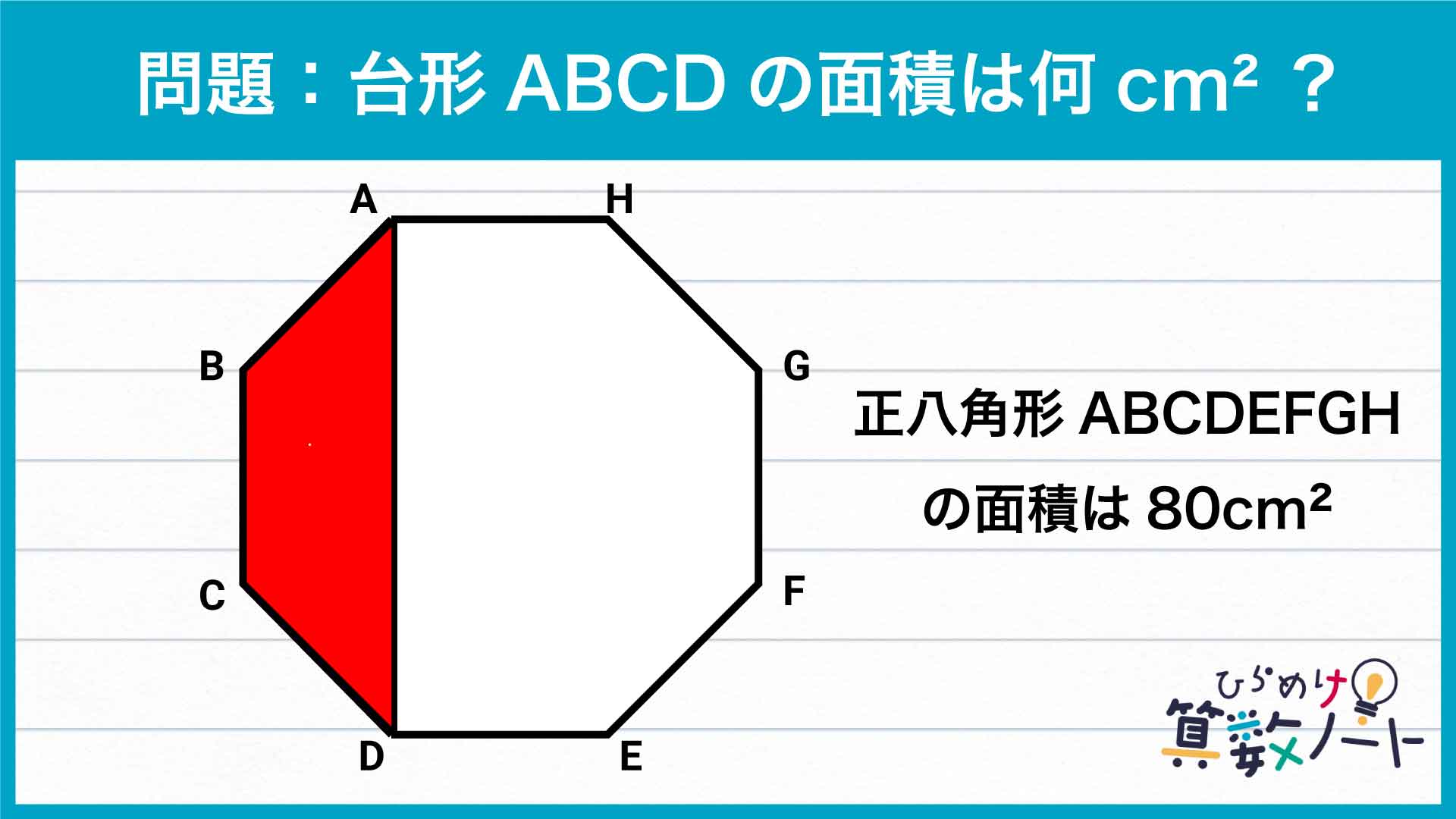
前ページ：【解答フォーム】自力で解きたい方はこちらへ！　以下は問題の答えです

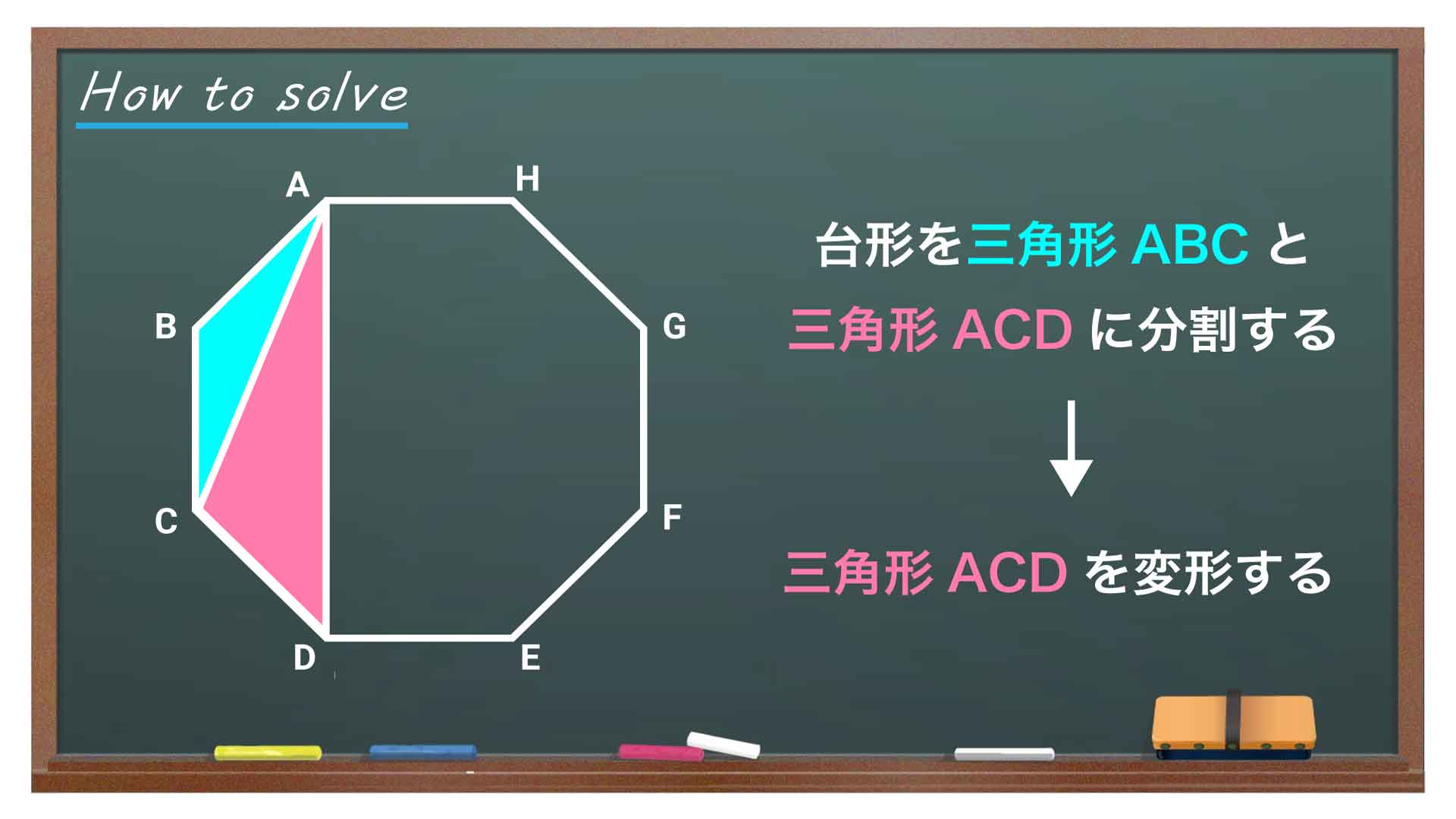
今回の問題の解き方をまとめた図がこちらです。ポイントは台形を分割し、三角形ACDの面積を変えずに変形することです。

この図の流れに沿って、解いていきましょう！

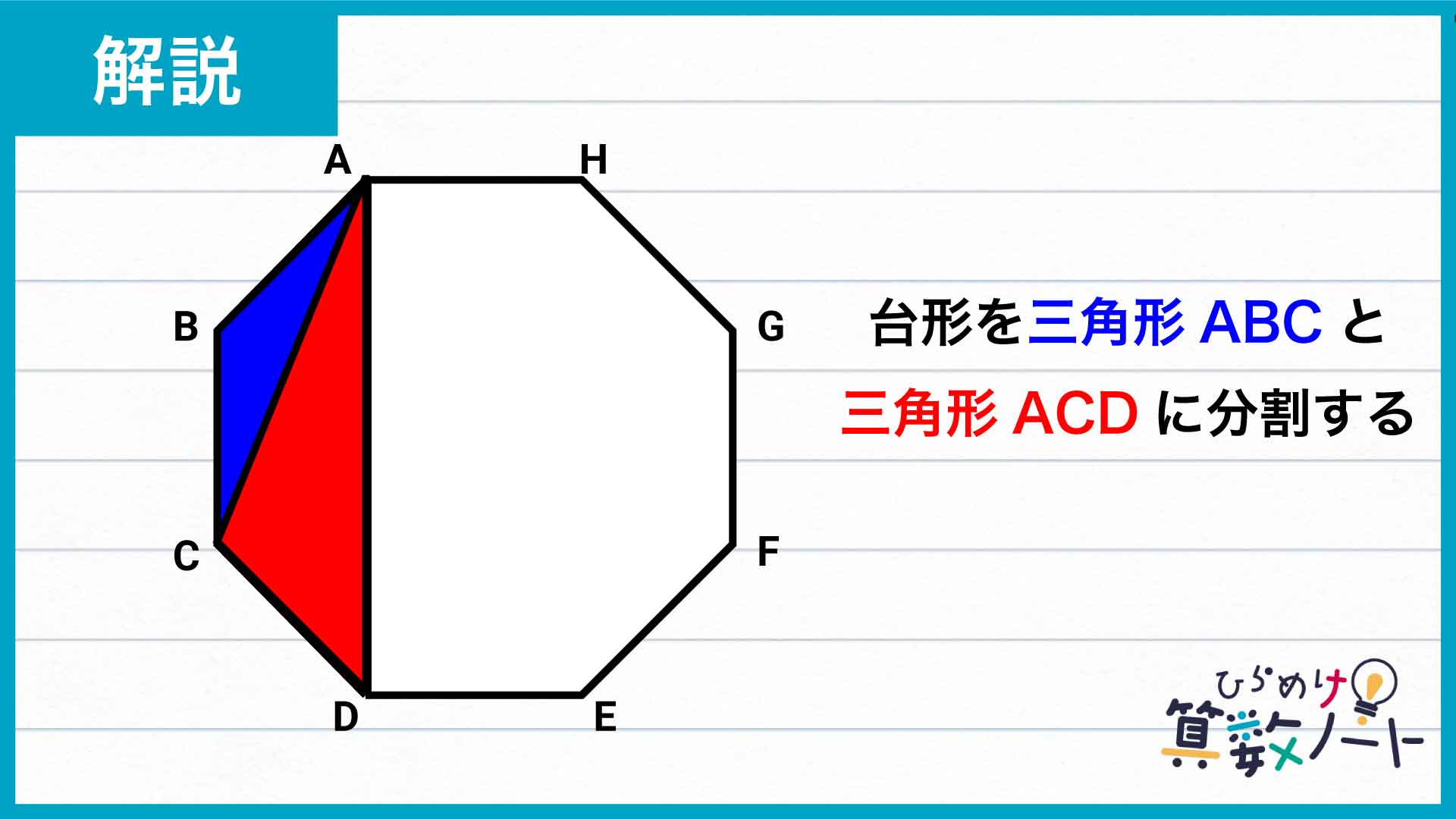
台形を2つの三角形に分割する

まずは、直線ACで、台形ABCDを三角形ABCと三角形ACDに分割します。

台形ABCDを面積を求めやすい形にするために、三角形ACDを変形させていきます。

直線ACと平行な直線は？

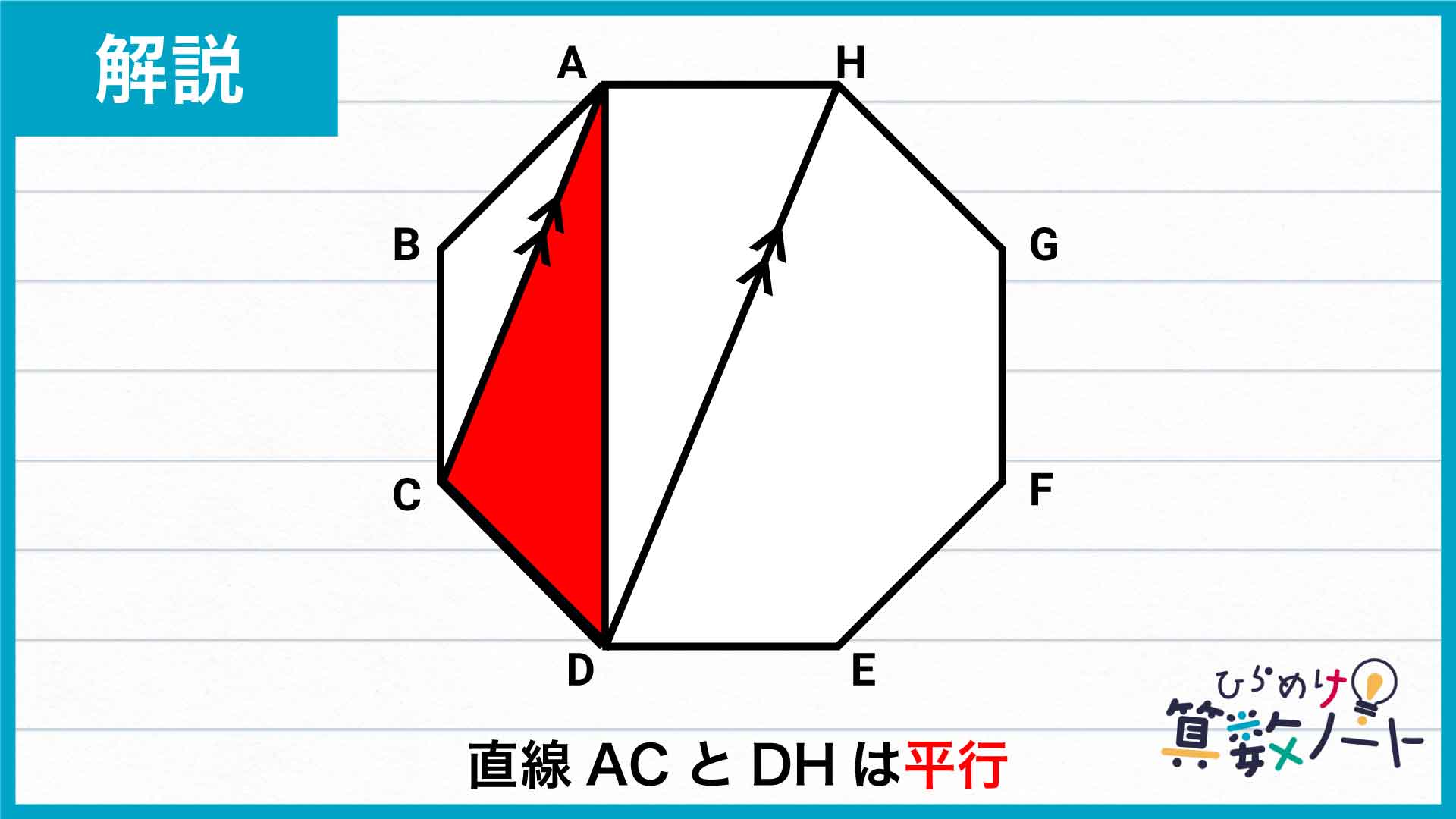
辺ACを三角形ACDの底辺とすると、点Dを辺ACと平行な直線上で動かせば高さは変わらず、面積も変わりません。

点Dを通り、辺ACと平行な直線は直線DHです。ACとDHが平行であることは、正八角形が直線BFに対して線対称であることからわかります。

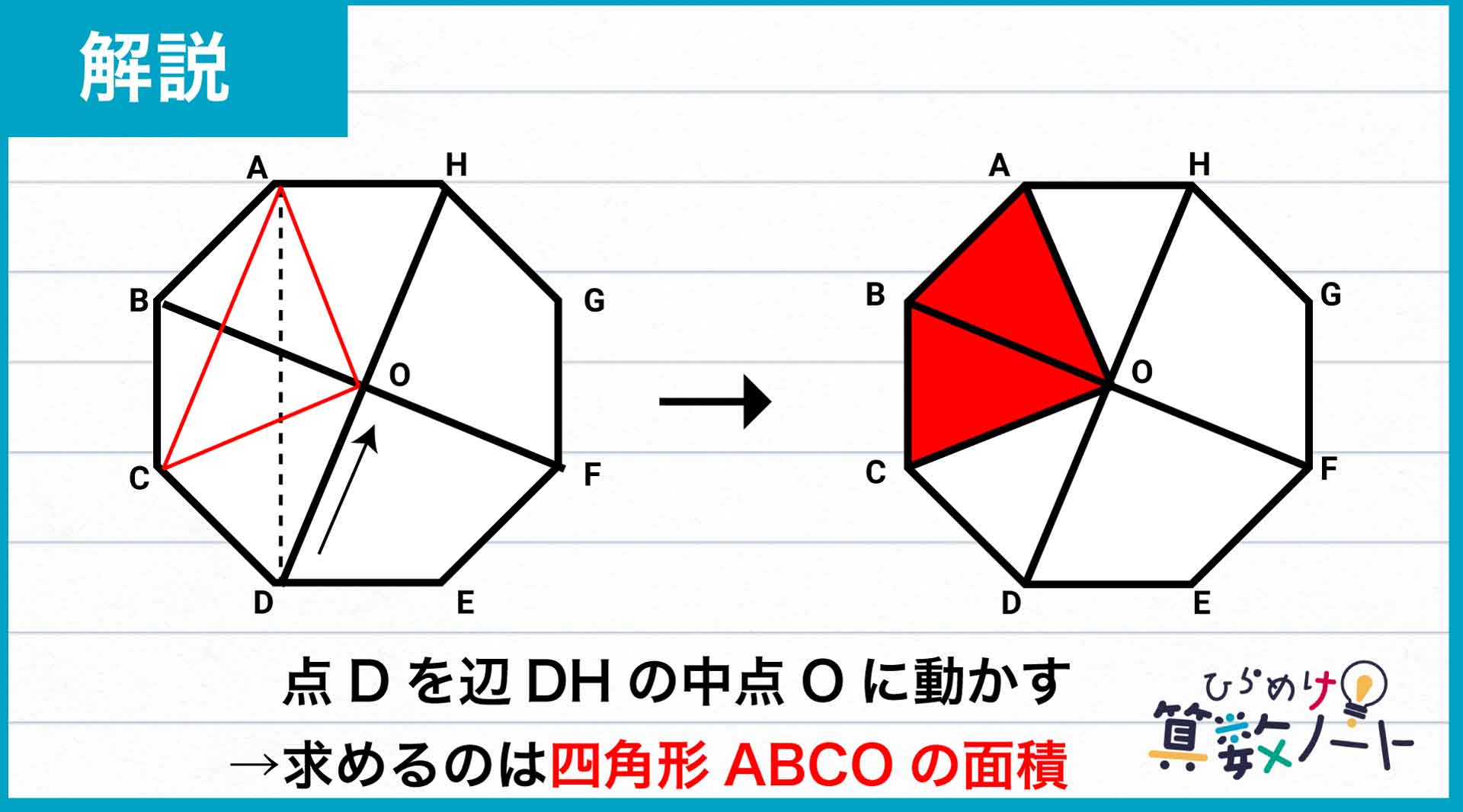
台形を面積が求めやすい形に変形するために、点Dを辺DHの中点（この点を点Oとします）に動かします。

変形させた図形と正八角形の面積の比は？

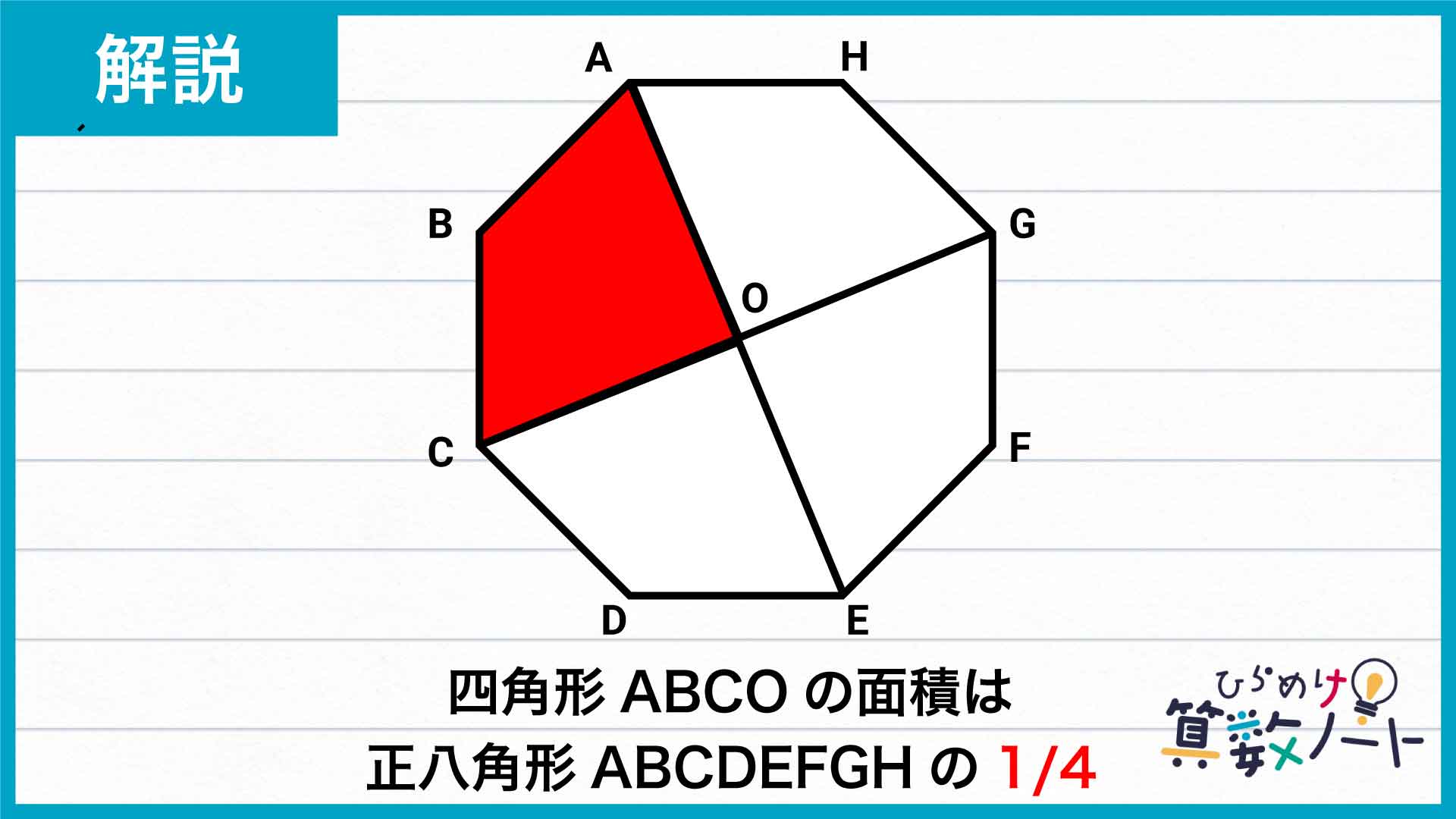
変形させた図形（四角形ABCO）は、正八角形ABCDEFGHを直線AEで2等分し、それをさらに直線CGで2等分した図形です。

したがって、四角形ABCOは正八角形ABCDEFGHの面積の1/4となります。

台形ABCDは四角形ABCOと面積が等しく、80÷4=20cm²です。

答え：20cm²

「ひらめけ！算数ノート」のバックナンバーはこちら！

【前回の算数ノートはこちら】

【あわせて読みたい】