解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
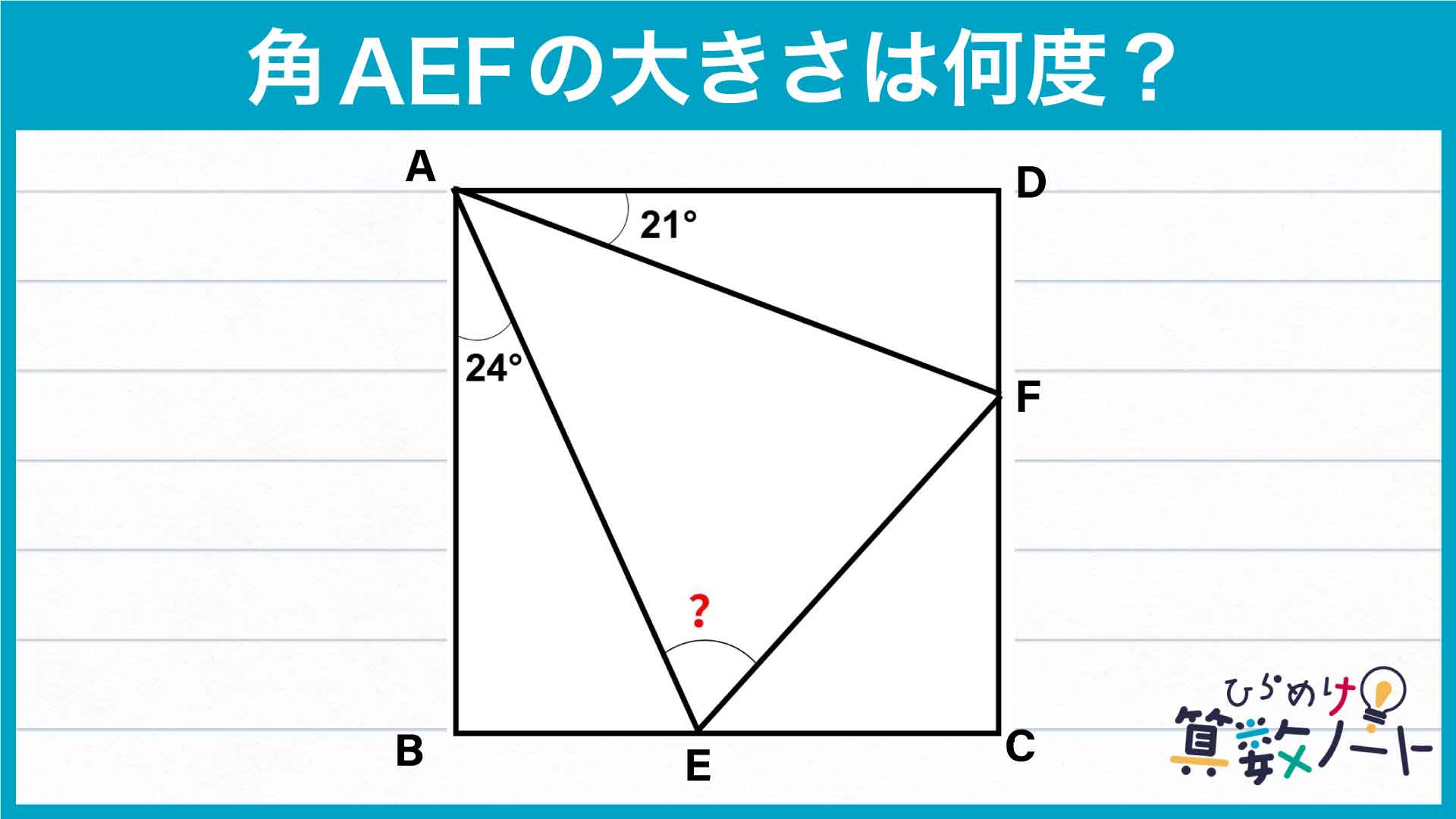
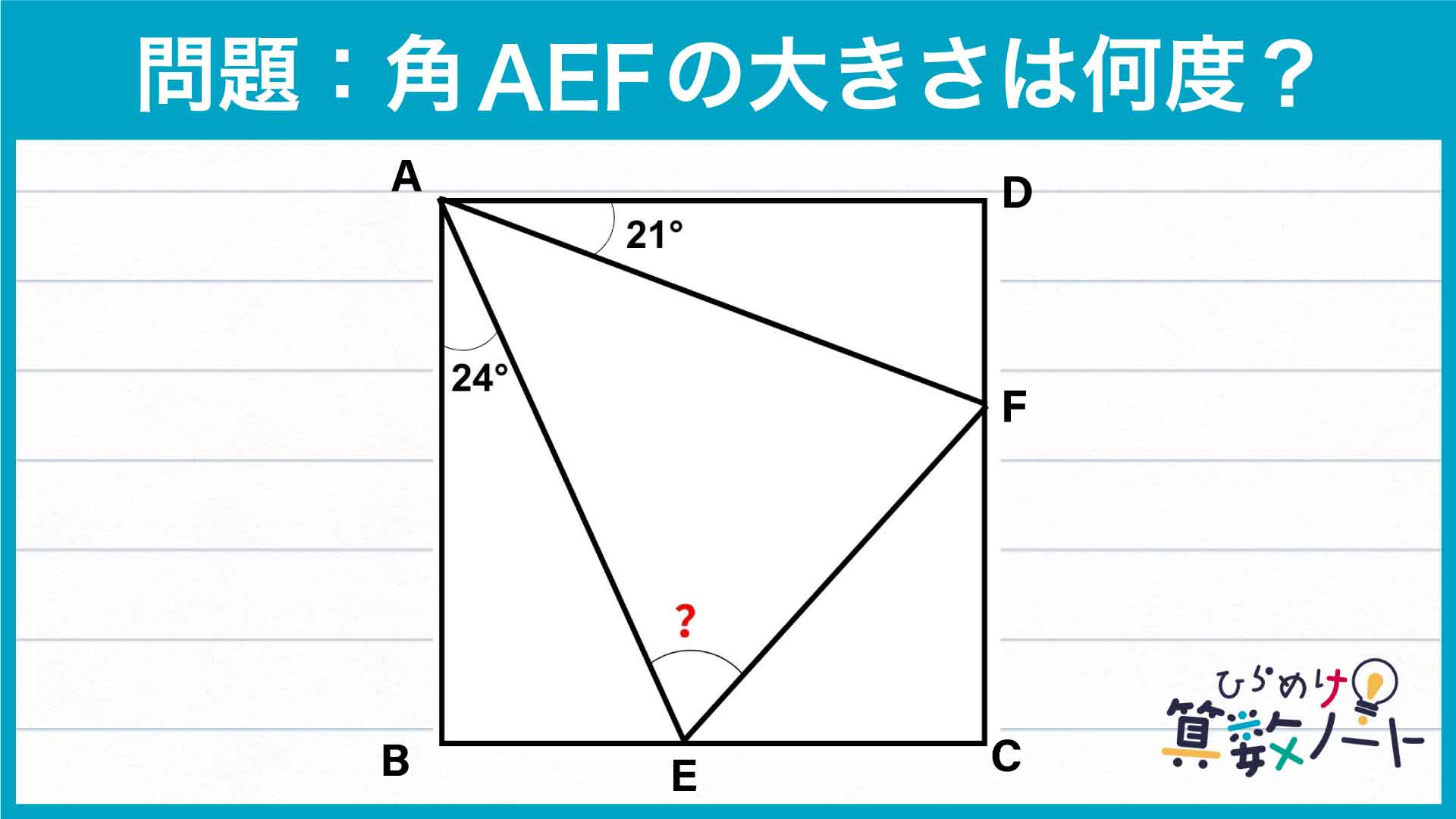
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
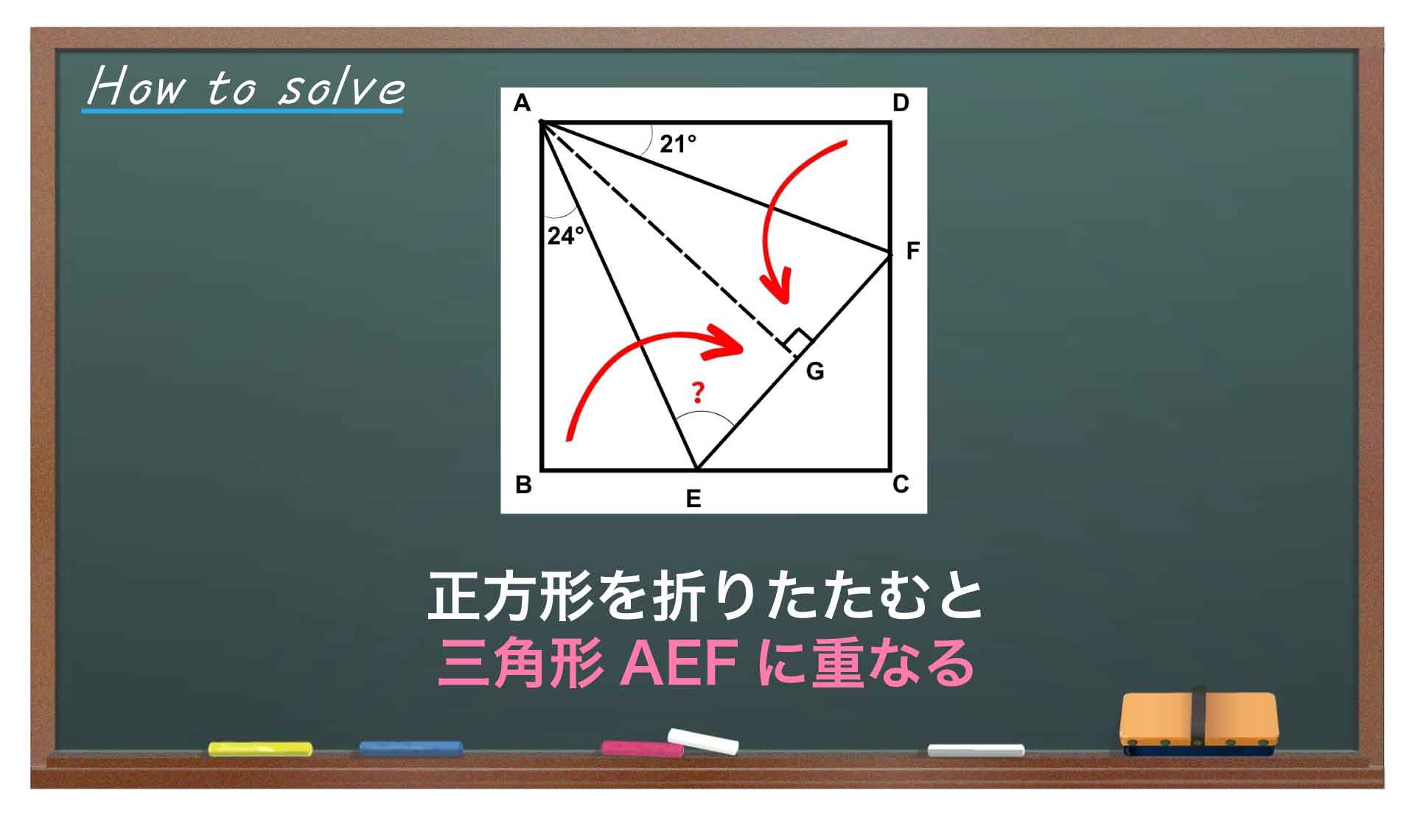
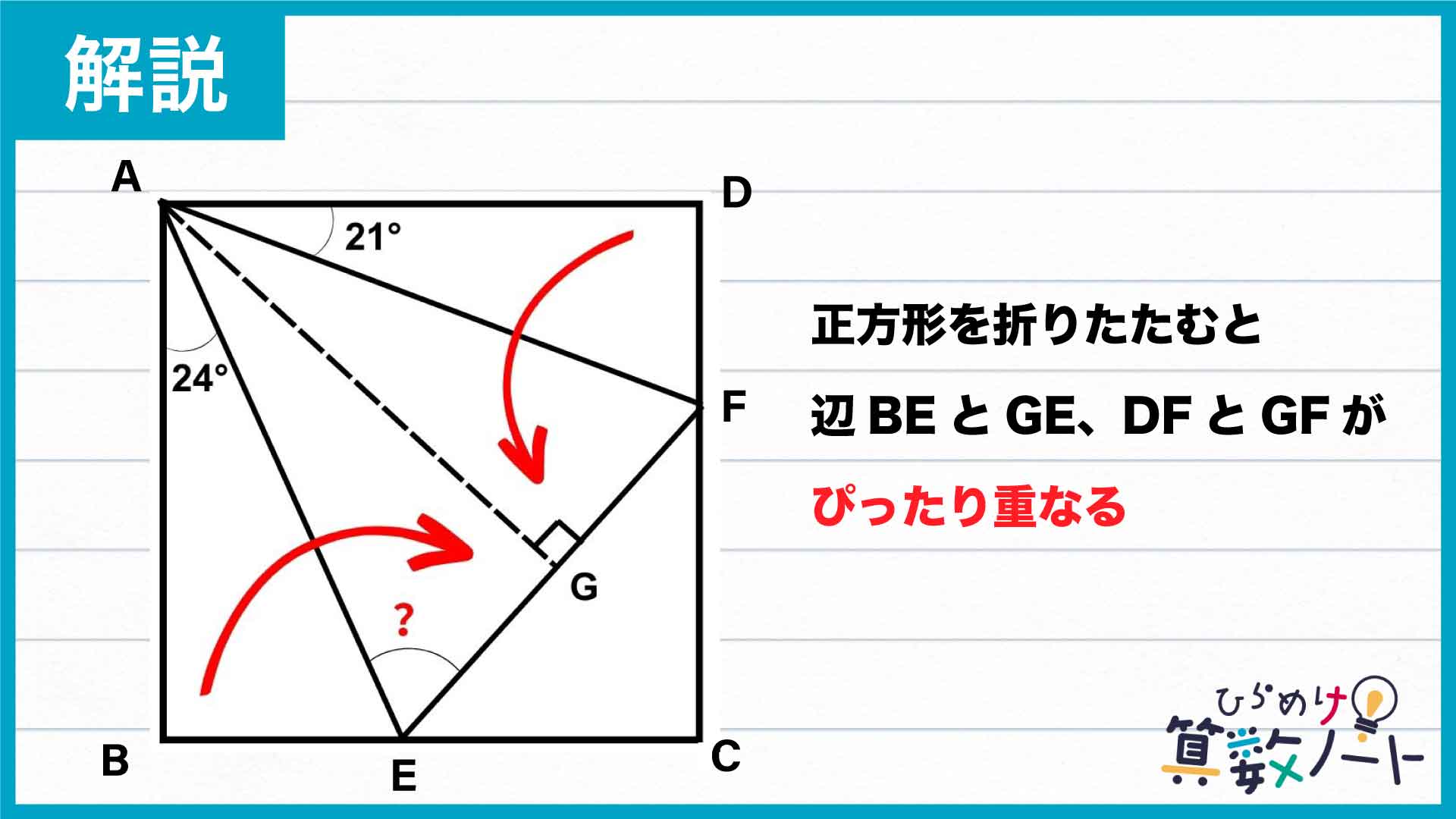
今回の問題の解き方をまとめた図がこちらです。ポイントは正方形を折りたたむと三角形AEFに重なることです。
この図の流れに沿って、解いていきましょう!
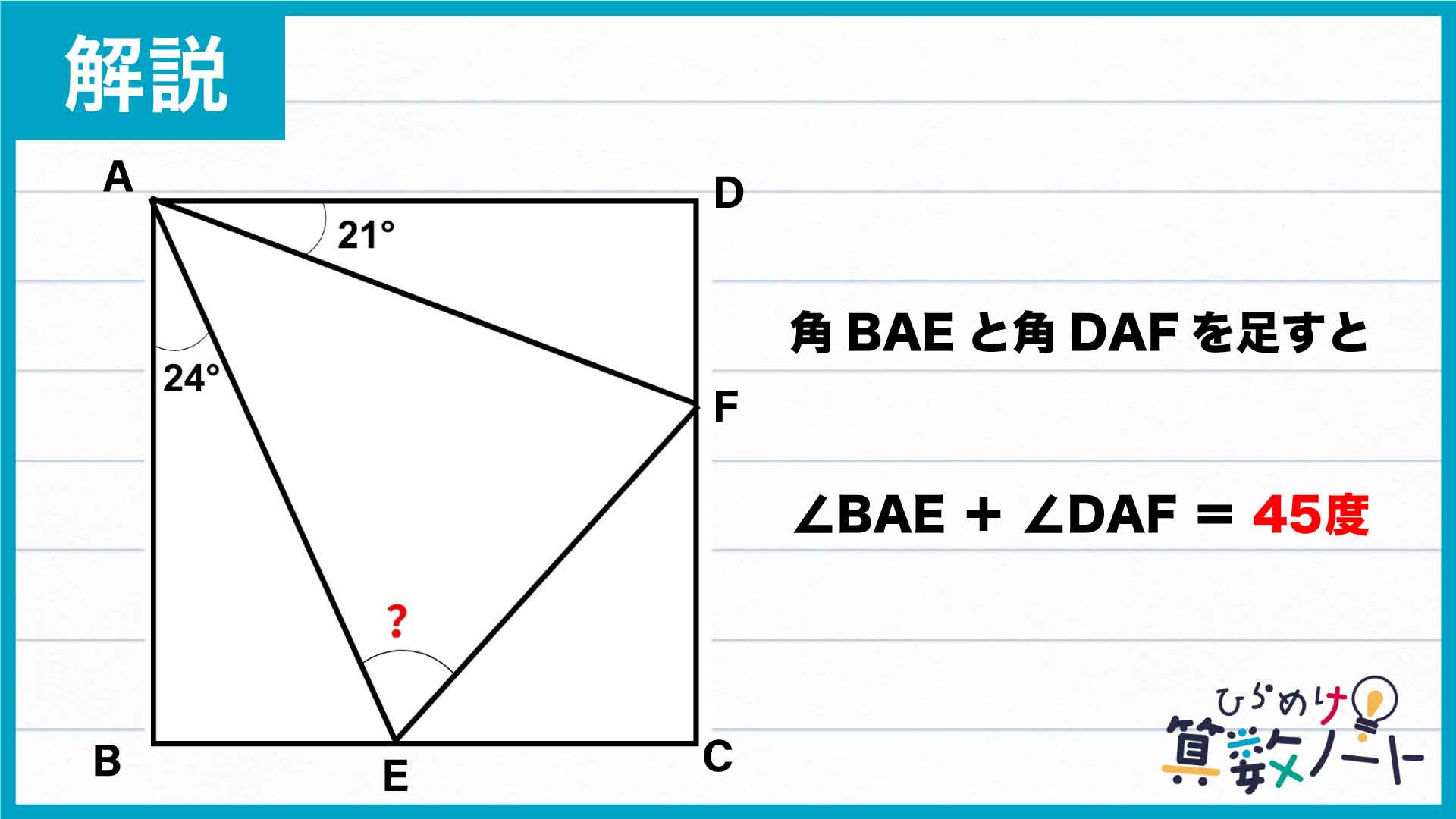
角BAEと角DAFを足すと?
まずは、角BAEと角DAFの和に着目しましょう。この2つの角の和は、24+21=45度です。
正方形を折りたたむ
角BAEと角DAFの和の45度は、90度(直角)のちょうど半分です。このことから、正方形を直線AE、AFで折ると、三角形AEFにぴったり重なることがわかります。
図のように、点Aから直線EFに垂線を下ろし、直線EFとの交点をGとします。すると、辺BEはGEに、辺DFはGFに重なります。
折りたたむとぴったり重なるということは……
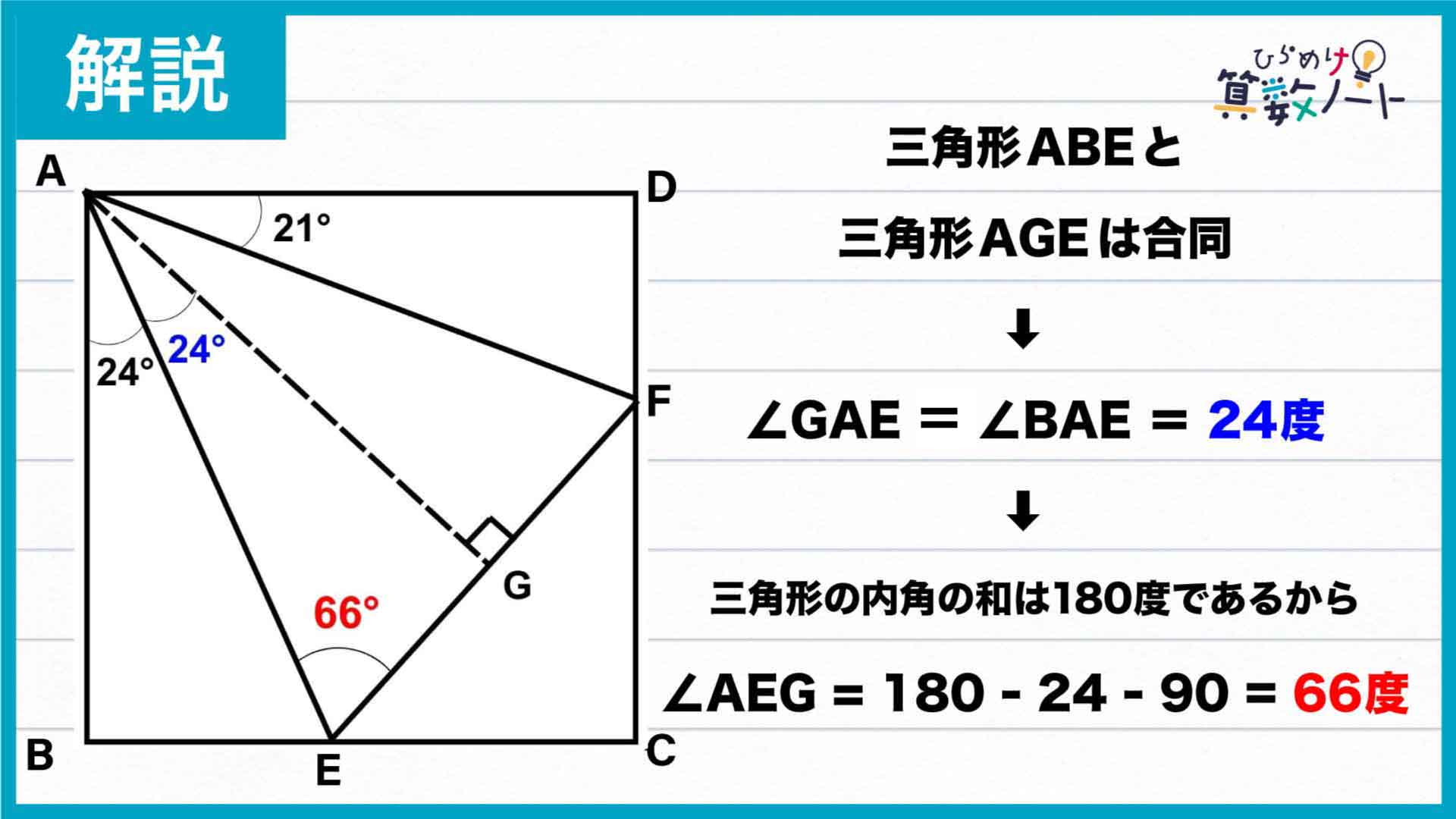
正方形を直線AEで折ると、辺BEがGEにぴったり重なることから、三角形ABEと三角形AGEは合同であるとわかります。
したがって、角GAE=角BAE=24度、角AGE=角ABE=90度です。
三角形AGEの内角の和が180度であることから、角AEG(角AEF)の大きさは、180-24-90=66度となります。
答え:66度
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)









.jpg)







