小学生でも解ける！4つの円の数字パズル、あなたはわかる？

問題はこちら

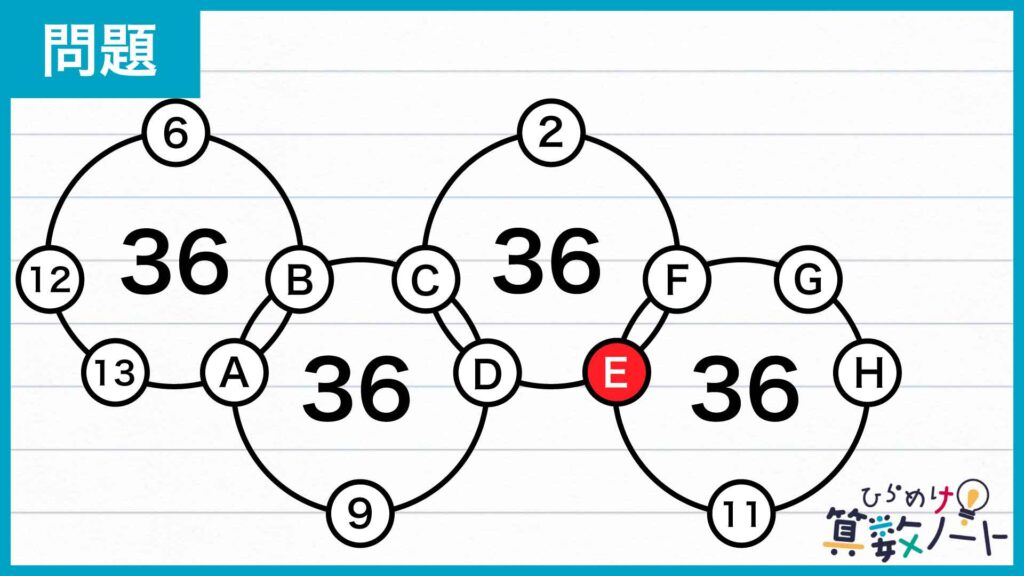
1ページ：【解答フォーム】自力で解きたい方はこちらへ！以下は問題の解説です

解説

それでは解説です。この問題のポイントは、各円の数字の合計が36になることを使って、未知の数の組み合わせを絞り込むことです。

結実子

まずは、わかっている数を使って、未知の数の和を求めましょう！

この問題の解き方をまとめた図がこちらです。

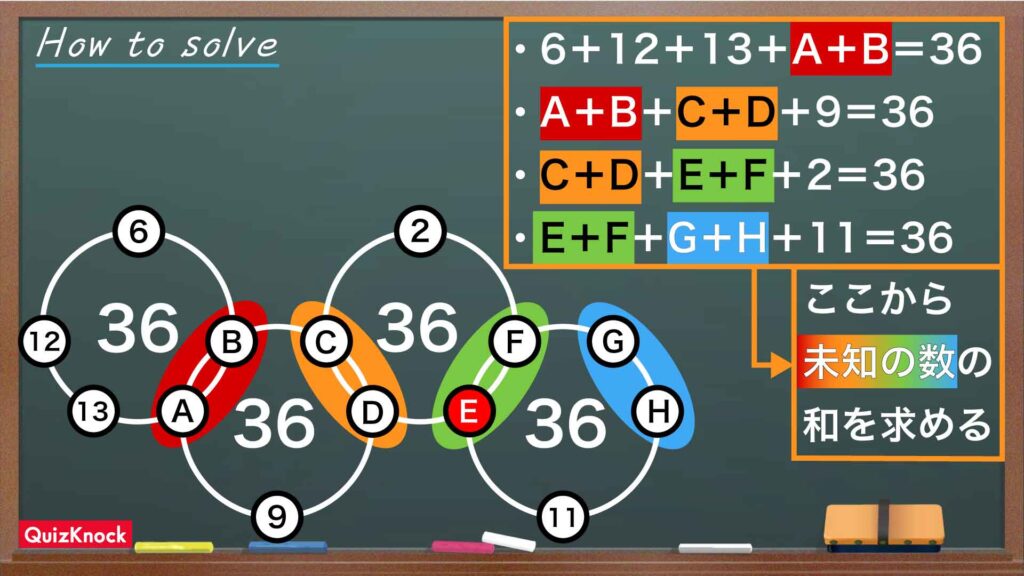
ステップ1：未知の数の和を求める

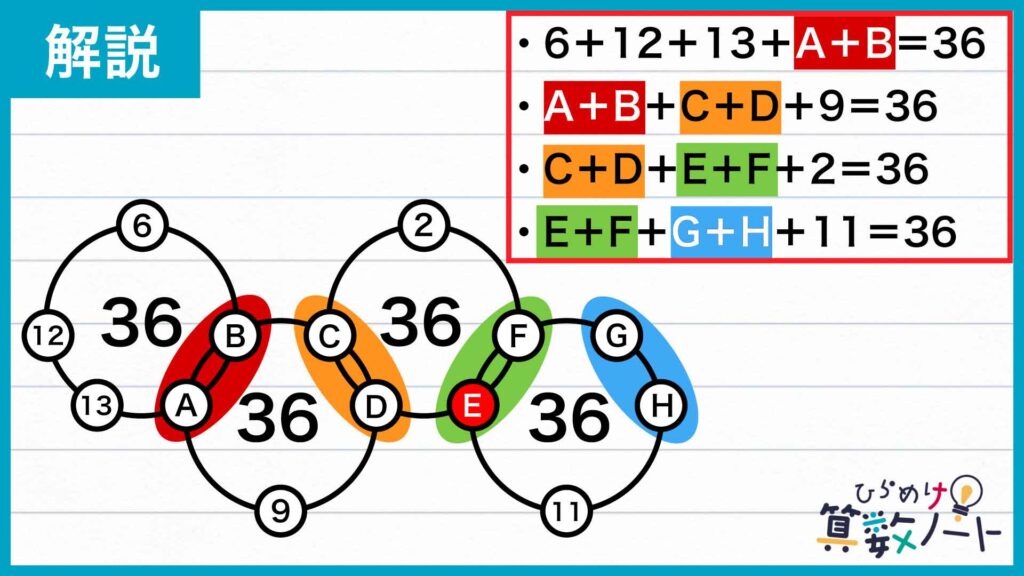
各円の合計が36なので、次のように計算できます。

6 + 12 + 13 + A + B = 36より、31 + A + B = 36なので
A + B = 5

A + B + C + D + 9 = 36より、5 + C + D + 9 = 36なので
C + D = 22

C + D + E + F + 2 = 36より、22 + E + F + 2 = 36なので
E + F = 12

E + F + G + H + 11 = 36より、12 + G + H + 11 = 36なので
G + H = 13

ステップ2：残りの数字を確認する

1〜14のうち、すでに使われている数は2、6、9、11、12、13です。

したがって、残りの数字は1、3、4、5、7、8、10、14です。

結実子

次に、この8つの数字から、和を作る組み合わせを探します！

ステップ3：A + B = 5、C + D = 22となる組み合わせを考える

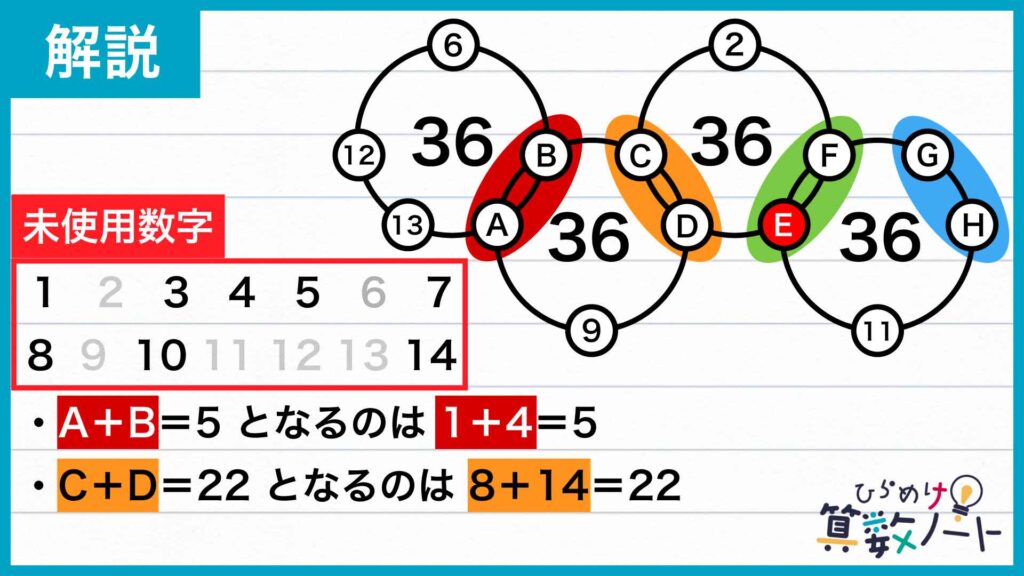
残りの数字（1、3、4、5、7、8、10、14）から、先ほど示したアルファベットの組み合わせを探していきます。

まず、合計が最小であるA + B = 5の組み合わせと、合計が最大であるC + D = 22の組み合わせを当てはめていきます。

A + B = 5となる組み合わせは1 + 4 = 5しかありません。

C + D = 22となる組み合わせは8 + 14 = 22しかありません。

これでA、B、C、Dの組み合わせが決まりました。残りの数字は3、5、7、10です。

ステップ4：E + F = 12、G + H = 13となる組み合わせを考える

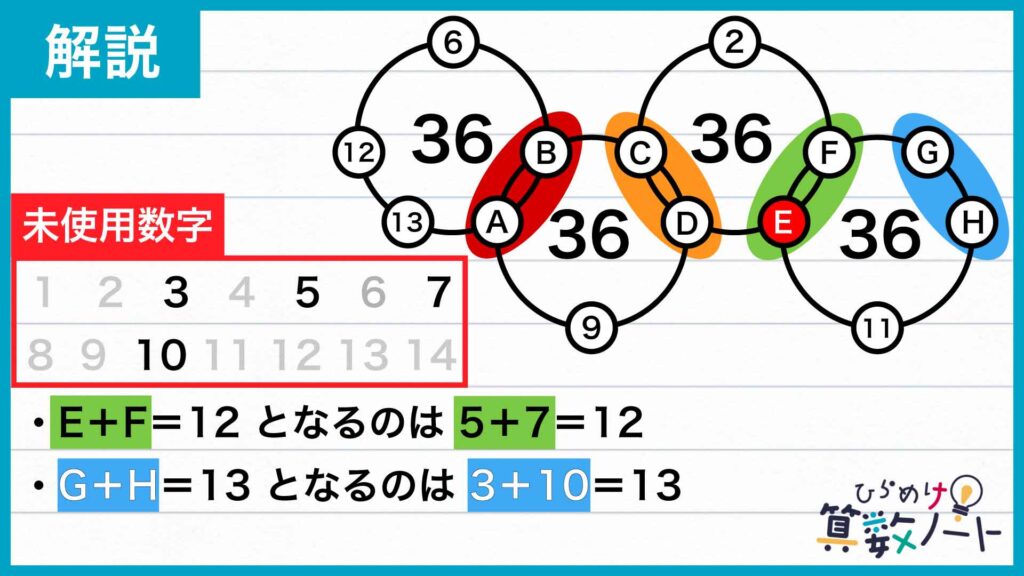
残りの数字（3、5、7、10）から、E + F = 12とG + H = 13を作る組み合わせを探します。

E + F = 12となる組み合わせは5 + 7 = 12のみです。

G + H = 13となる組み合わせは3 + 10 = 13のみです。

よって、EとFは5と7の組み合わせになります。問題文で「EよりもFの数が小さい」と示されていますので、E = 7、F = 5が確定します。

答え：7

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】