想定解は「フラクタル構造を持っている」ということです。
フラクタルとは、一部が全体と自己相似な構造を持っている図形のことです。たとえば左の図形は、シェルピンスキーの三角形と呼ばれるものです。この図形を4等分したものは元の図形と見分けがつかないです。右の写真では、シダの葉の分岐した1つ1つは元の葉と同じ形をしています。
Via/ https://commons.wikimedia.org/wiki/File:Sierpinski_zoom.gif
上のアニメーションでは、シェルピンスキーの三角形をどんなに拡大して、元と同じ図形が現れます。自己相似とはこういうことです。
フラクタルは「とても複雑な図形」ということもできます。複雑なのでよく見ようと拡大しても無限に複雑な形をしていてきりがないもののことです。
たとえば、雲はフラクタルです。
雲はフラクタルである
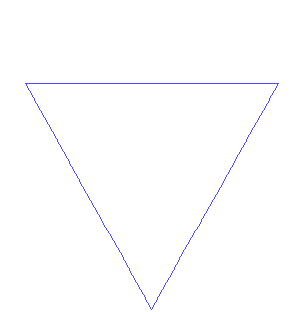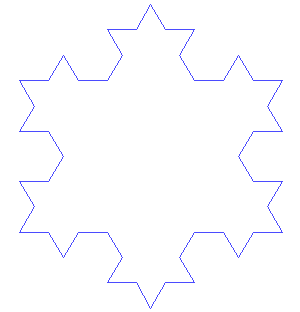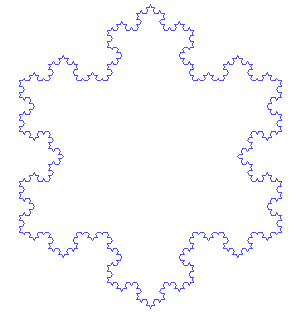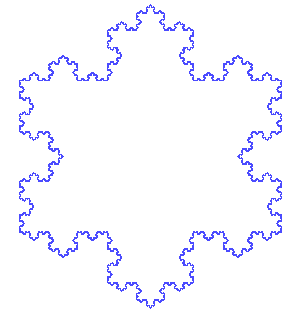
これはコッホ曲線と呼ばれるフラクタル図形を作っていくアニメーションです。コッホ曲線は線分を3等分し分割した2メンガーのスポンジ
Via/ https://commons.wikimedia.org/wiki/File:Menger.png
シェルピンスキーの三角形やコッホ曲線は平面のフラクタルでしたが、メンガーのスポンジは立体のフラクタルです。立方体の中央の3分の1に穴をあけ、残りの3分の1にさらに穴をあけ……、と繰り返した極限がメンガーのスポンジです。
数学の極限を学んだ人はこの立体の表面積と体積を計算してみてください。表面積は無限大に、体積は0になるはずです。体積が0なのに表面積が無限大というのはとても違和感があります。しかし先程述べたようにフラクタル自体が極限的な操作による空想上の産物にすぎないので（自然界に見られるフラクタルはあくまで近似）、まあそういうことだと思ってください。
マンデルブロ集合
Via/ https://commons.wikimedia.org/wiki/File:Mandel_zoom_00_mandelbrot_set.jpg
コッホ曲線やメンガーのスポンジより高度（？）な数学的操作で得られるフラクタル図形にマンデルブロ集合があります。これは複素平面上で「ある条件」を満たす点をプロットしていったものです。
マンデルブロ集合を拡大するとさまざまなパターンが見られます。こんな不思議なパターンもあります。
Via/ https://commons.wikimedia.org/wiki/File:Mandel_zoom_11_satellite_double_spiral.jpg?uselang=ja
ちなみに、マンデルブロ集合に名を残すブノワ・マンデルブロ氏は、何を隠そう「フラクタル」の概念を考案した人です。
バーンズリーのシダ
Via https://commons.wikimedia.org/wiki/File:Barnsley_fern_plotted_with_VisSim.PNG
最初に見せたシダの写真のような図形も、「ある条件を満たす点をプロットしていく」という数学的な操作で書くことができます。これが、「バーンズリーのシダ」です。単なる数学的な操作でこんな絵が描けてしまうのは、とても興味深いです。
いかがでしたでしょうか。フラクタル図形はその数学的な背景を考えなくても、単に見ているだけで不思議な気分に浸れるものです。興味を持った人にはマンデルブロが書いた『フラクタル幾何学（上・下）』（ちくま学芸文庫）がオススメです。
復習
