小学生で解ける「図形の面積」を求める問題にチャレンジ！

問題はこちら

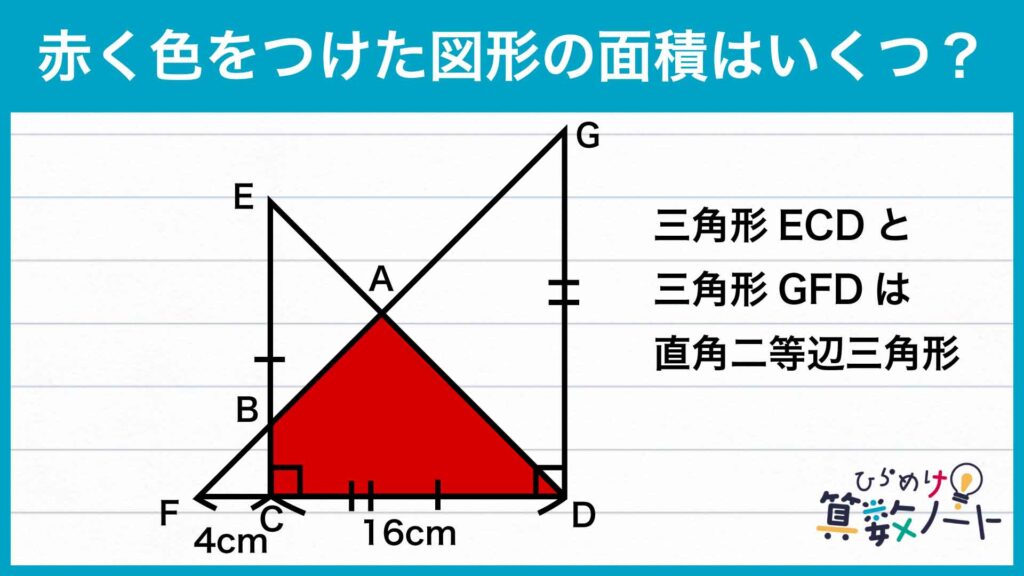
1ページ目：自力で解きたい方はこちらへ！　以下は問題の解説です

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

今回の問題を解くうえで重要なポイントを以下にまとめました。

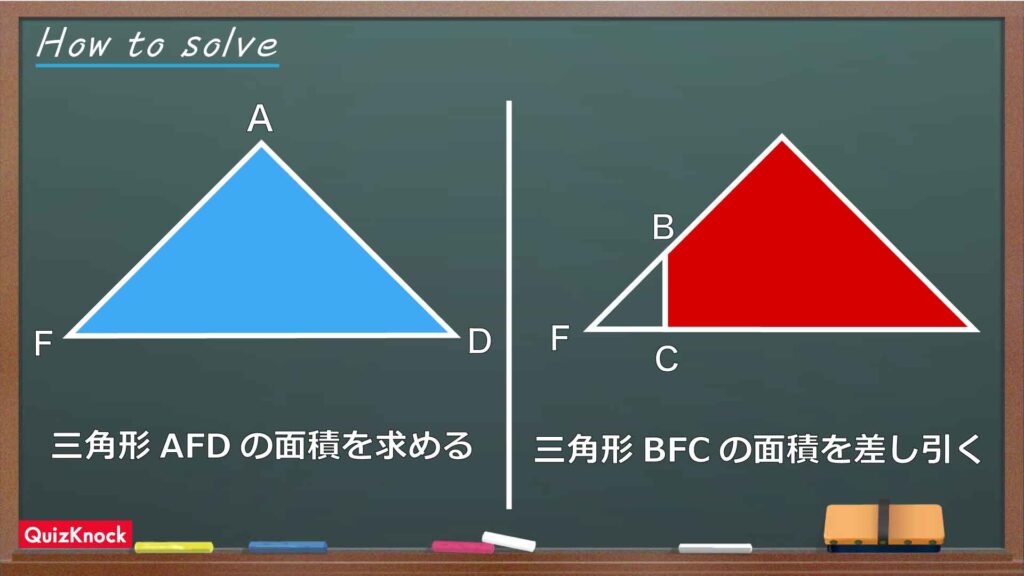
整理すると、

• 三角形AFDの面積を求める
• 三角形BFCの面積を差し引く

の2点です。これらのポイントを踏まえながら、問題を解いていきましょう。

三角形AFDの面積を求める

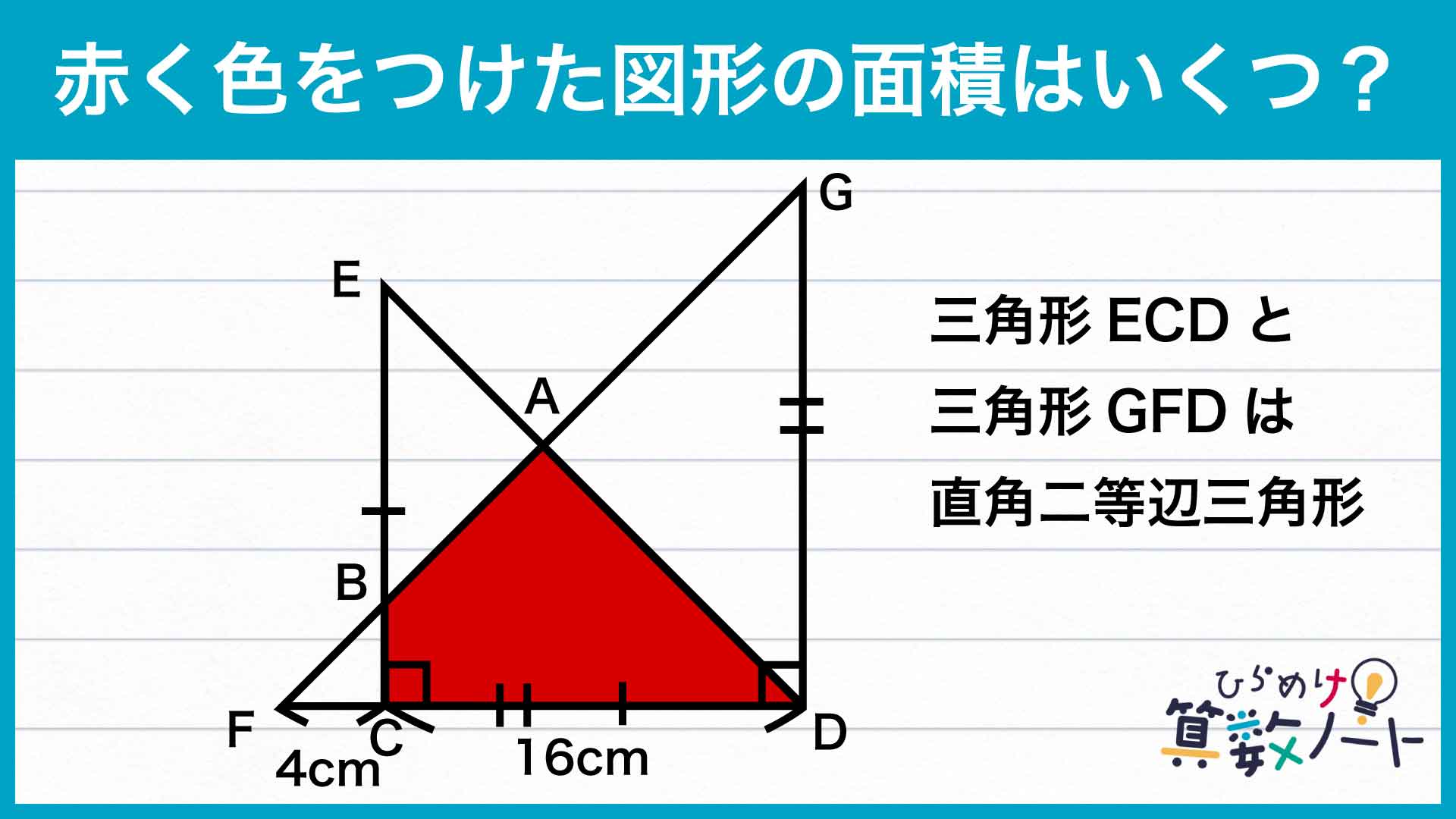
四角形ABCDの面積は、三角形AFDの面積から三角形BFCの面積を差し引くことにより求めることができます。そこで、まずは下のような三角形AFDに注目します。

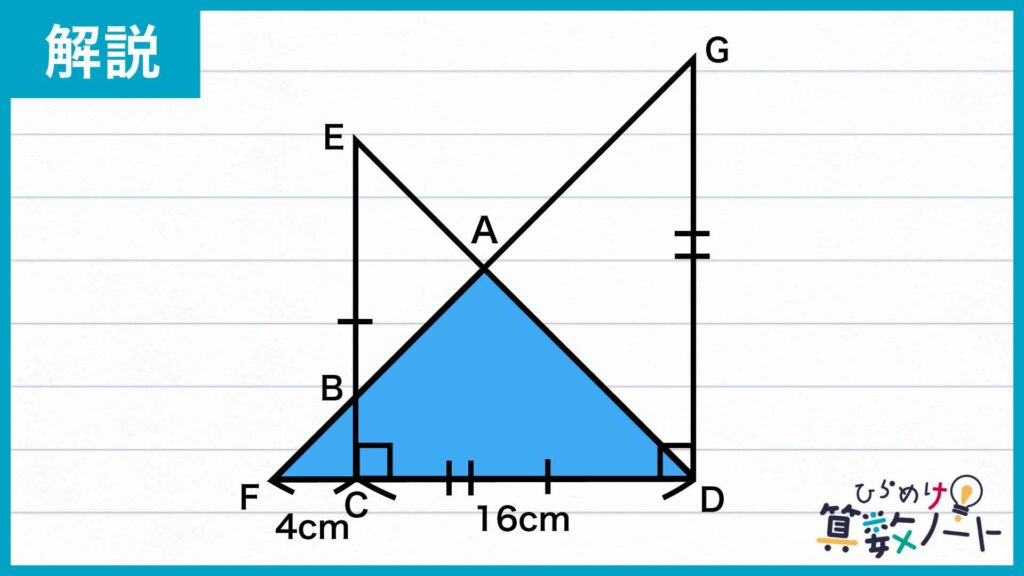
ここから、三角形AFDの面積を求めていきます。

点AからFDに垂線を下ろし、垂線とFDとの交点を点Hと置きます。FDを三角形AFDの底辺とみなすと、三角形AFDの高さはAHの長さになります。

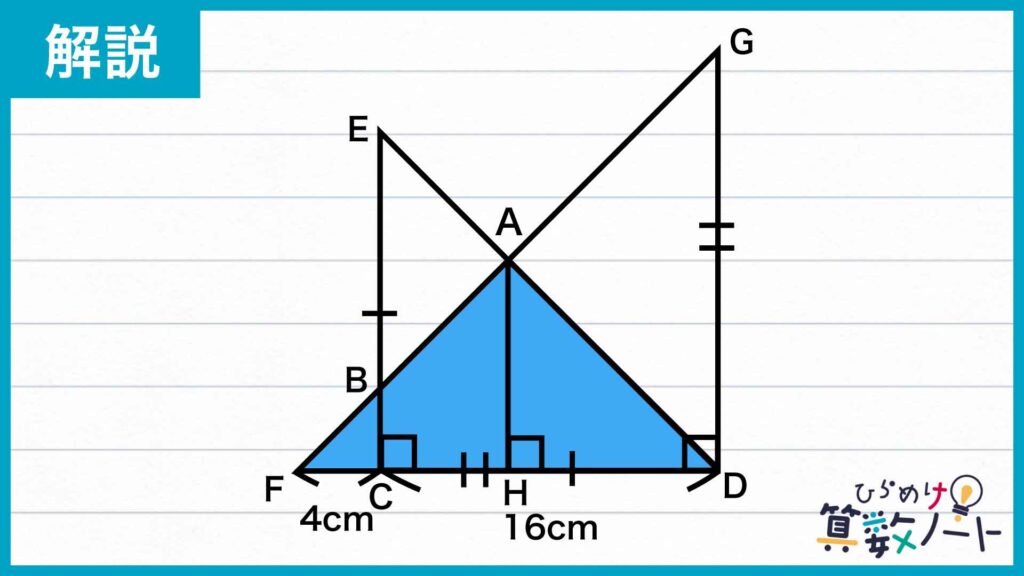
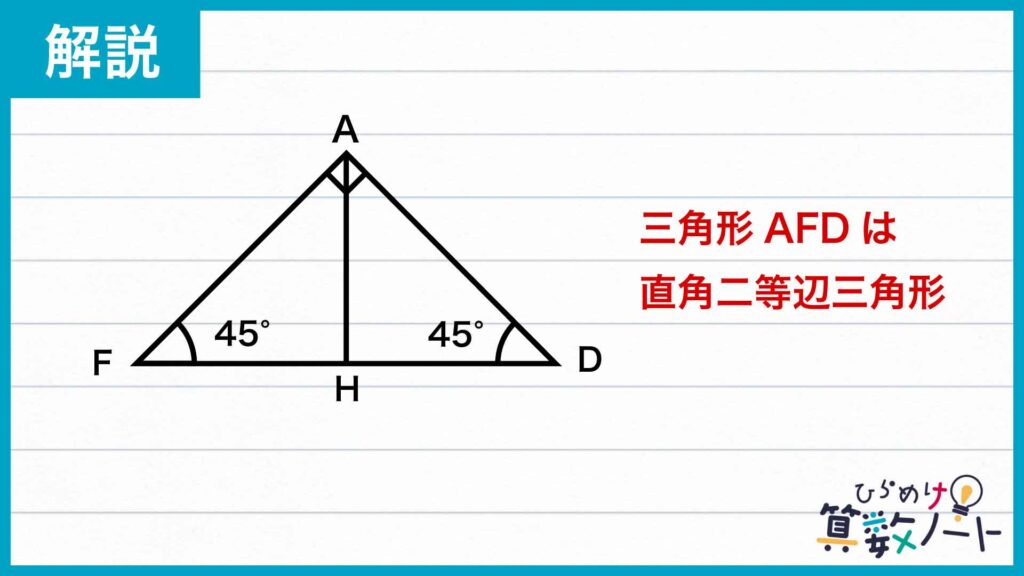
ここで、三角形ECDは問題の条件から直角二等辺三角形なので、角ADF=45度です。また、三角形GFDも直角二等辺三角形なので、角AFD=45度です。したがって、角DAF=180-45-45=90度であるので、三角形AFDは直角二等辺三角形になることがわかります。

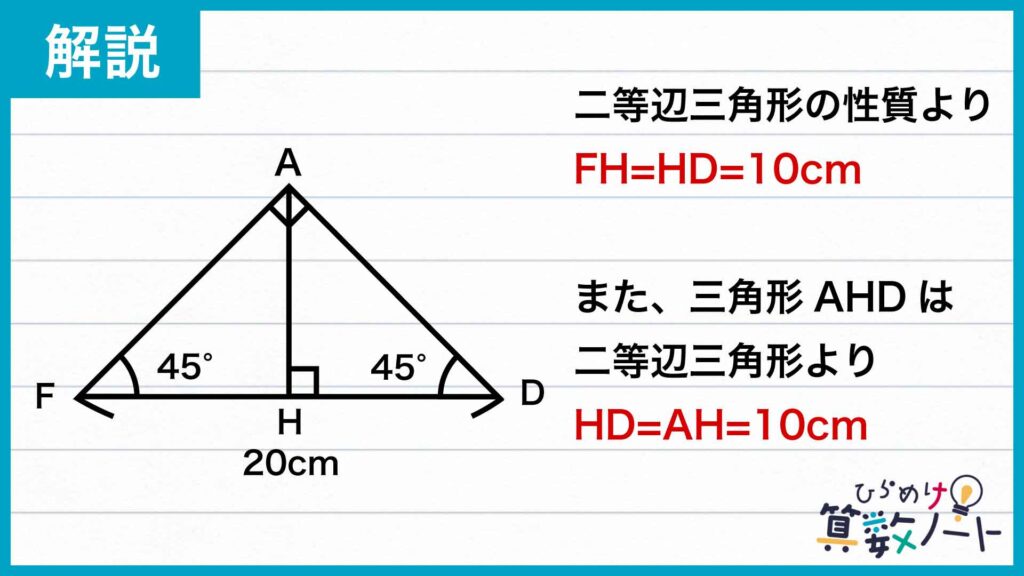
ここで、AHは点AからFDに下ろした垂線であるので、二等辺三角形の性質から、点HはFDをちょうど二等分する点になります。したがって、FD=FC+CD=4+16=20cmより、FH=HD=10cmになります。さらに、角ADF=45度、角AHD=90度より、三角形AHDは直角二等辺三角形になるので、HD=AH=10cmです。

したがって、三角形AFDの面積は、（FDの長さ）×（AHの長さ）÷2=20×10÷2=100cm²になります。

三角形BFCを差し引く

次に、三角形BFCの面積を求めましょう。

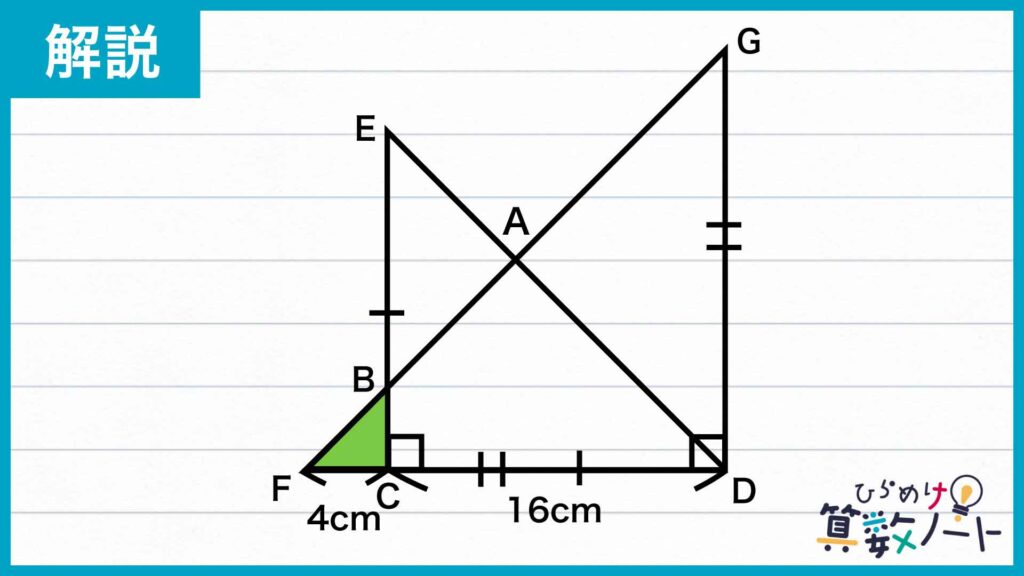
次に、三角形GFDは直角二等辺三角形なので、角BFC=45度です。また、三角形ECDも直角二等辺三角形であるので、角BCF=90度です。したがって、角CBFの大きさは180-(45+90)=45度であることがわかります。

よって、三角形BFCはCF=BCの直角二等辺三角形であることがわかります。

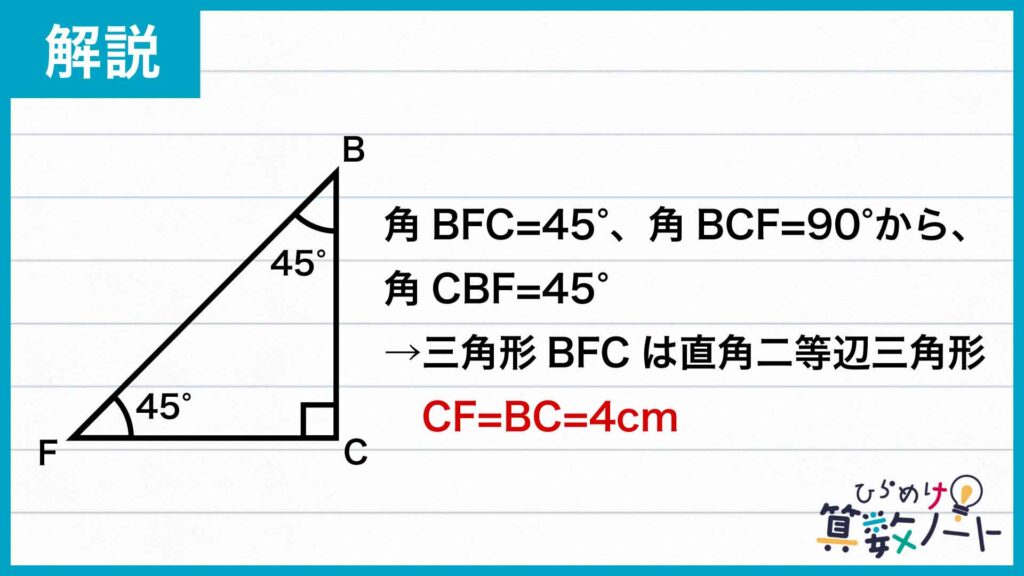
したがって、三角形BFCの面積は、（BCの長さ）×（CFの長さ）÷2=4×4÷2=8cm²になります。

よって、求める答えは三角形AFDの面積から三角形BFCの面積を差し引くことで、100-8=92cm²と求められます。

答え：92cm²

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】