問題はこちら
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の解説です
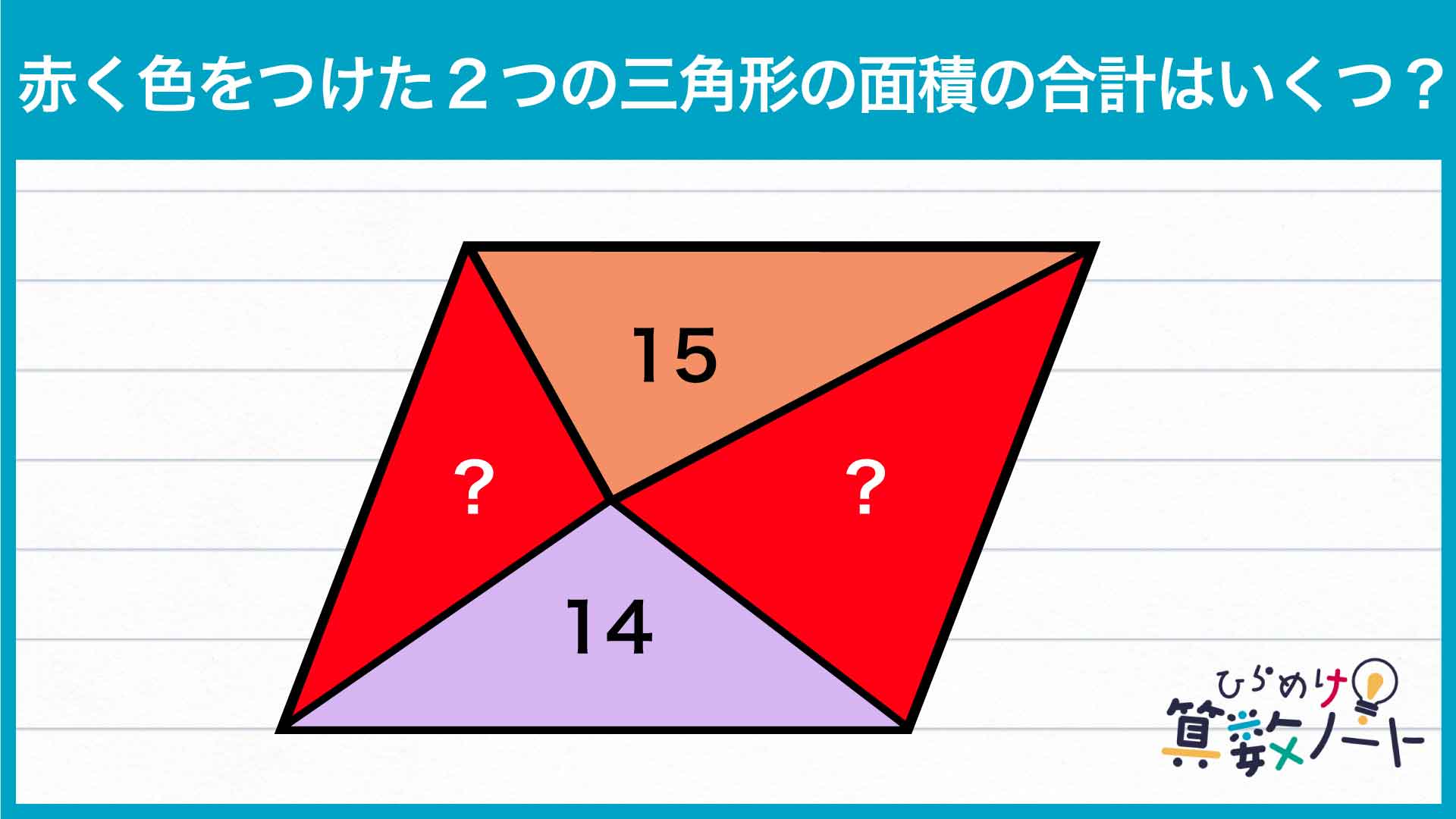
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
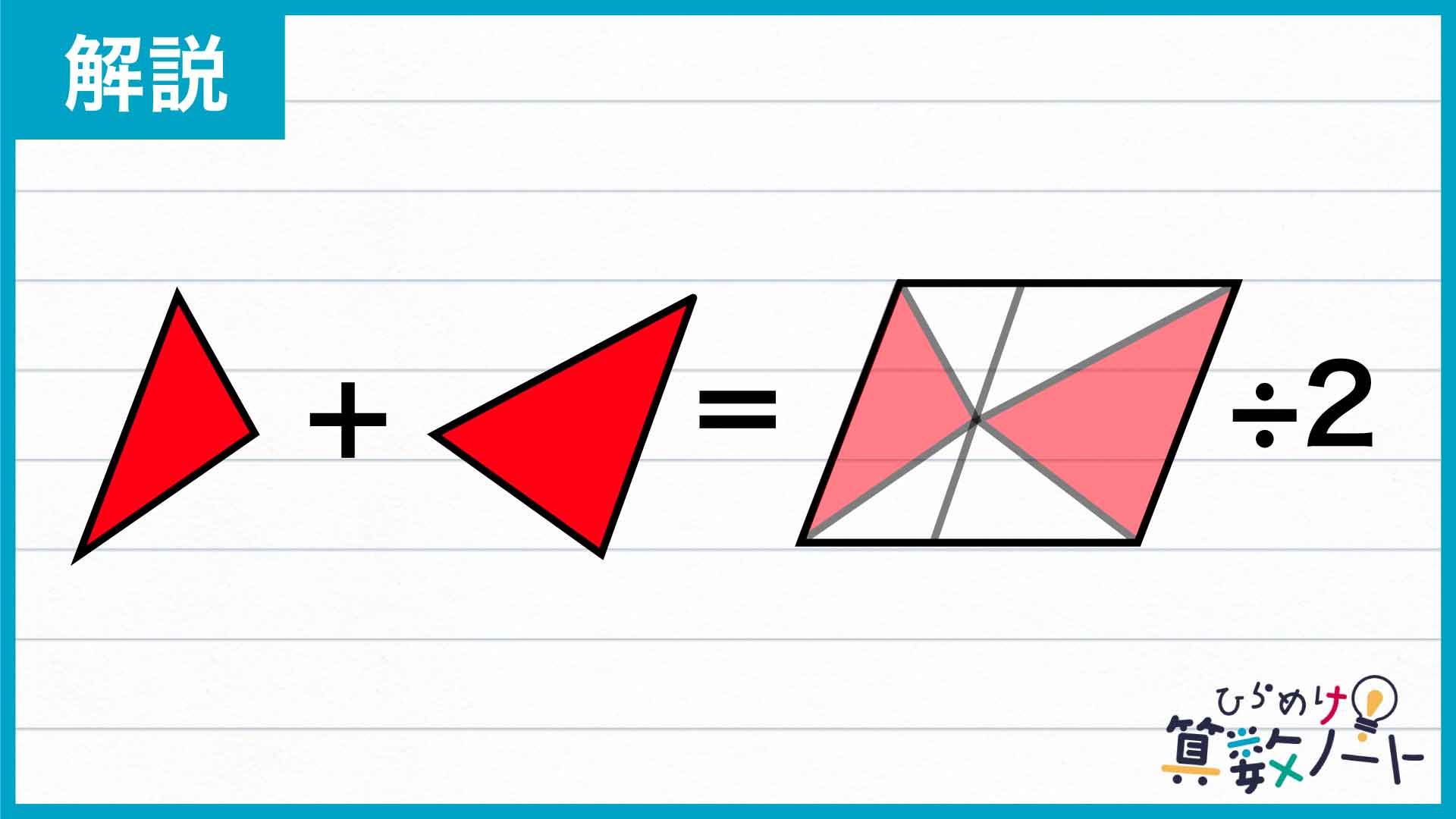
この問題の解き方をまとめた図がこちらです。
ポイントは、向かい合う三角形の面積の合計と平行四辺形の面積の関係を考えることです。
では、このポイントを踏まえつつ解いていきましょう!
解説はこちら
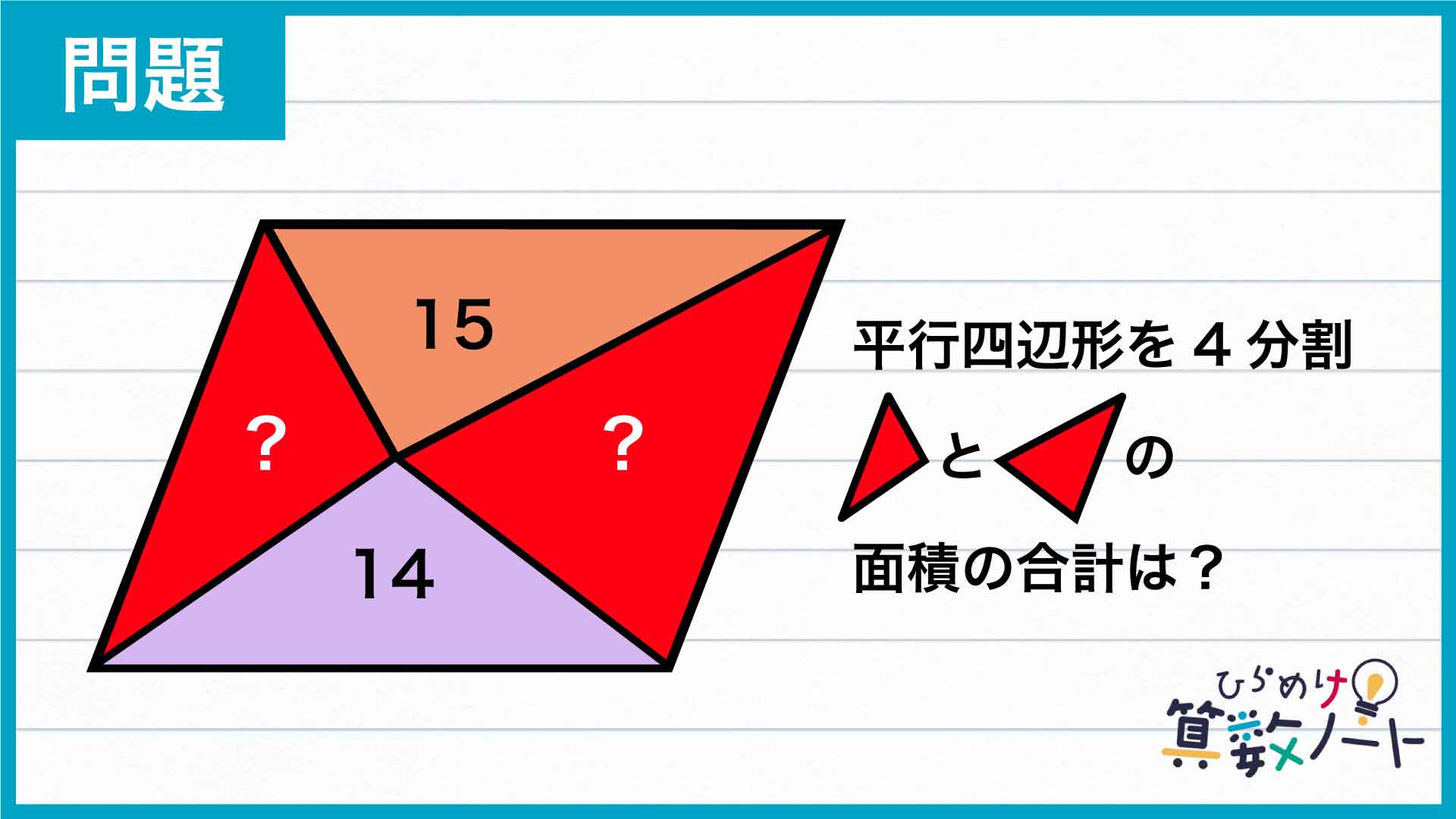
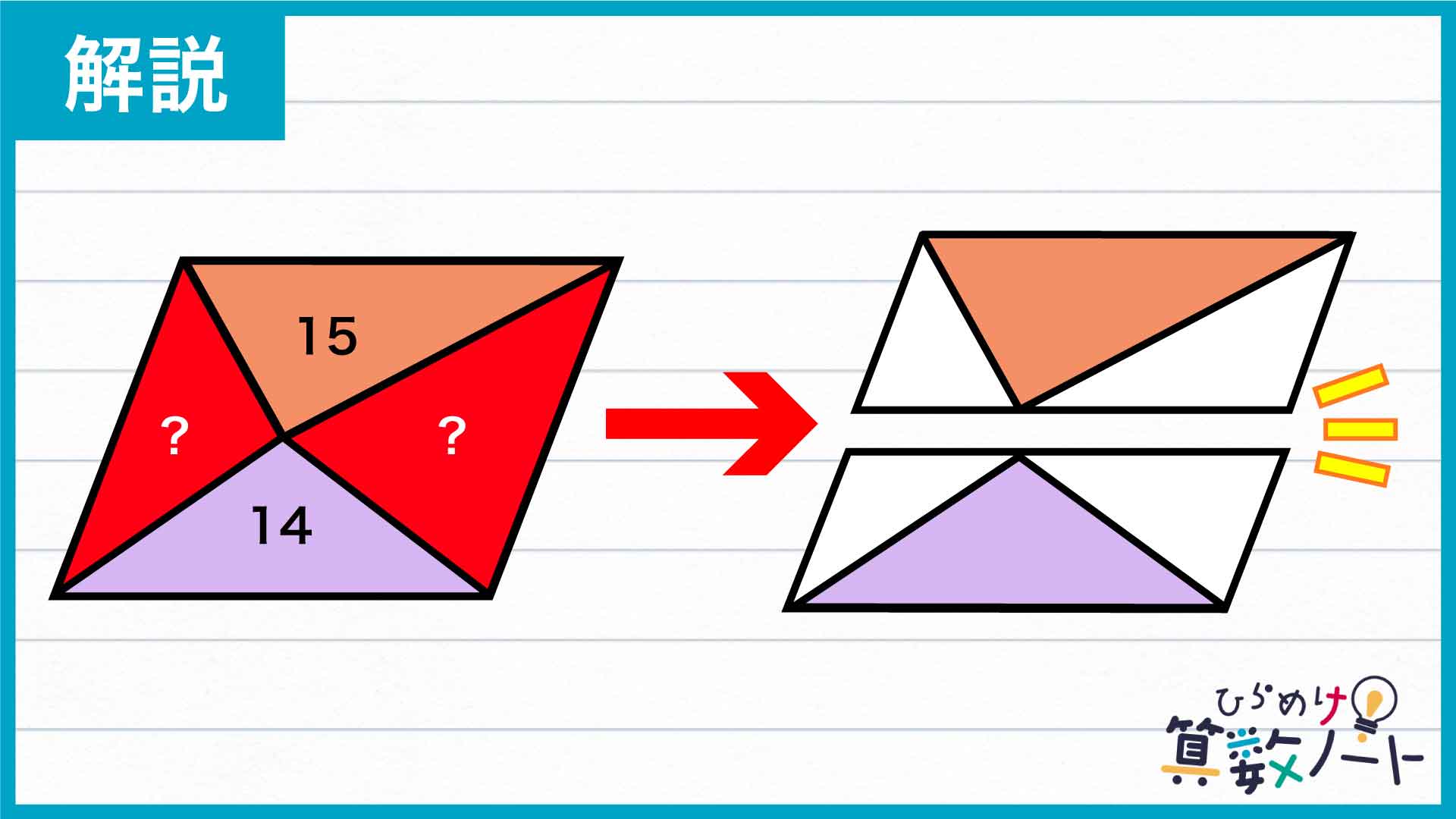
分割する前の平行四辺形は底辺の長さも高さもわからないため、このままでは答えを導けそうにありません。そこで、面積がわかっている三角形をうまく利用するため、下の図のように平行四辺形を分割しなおしてみます。
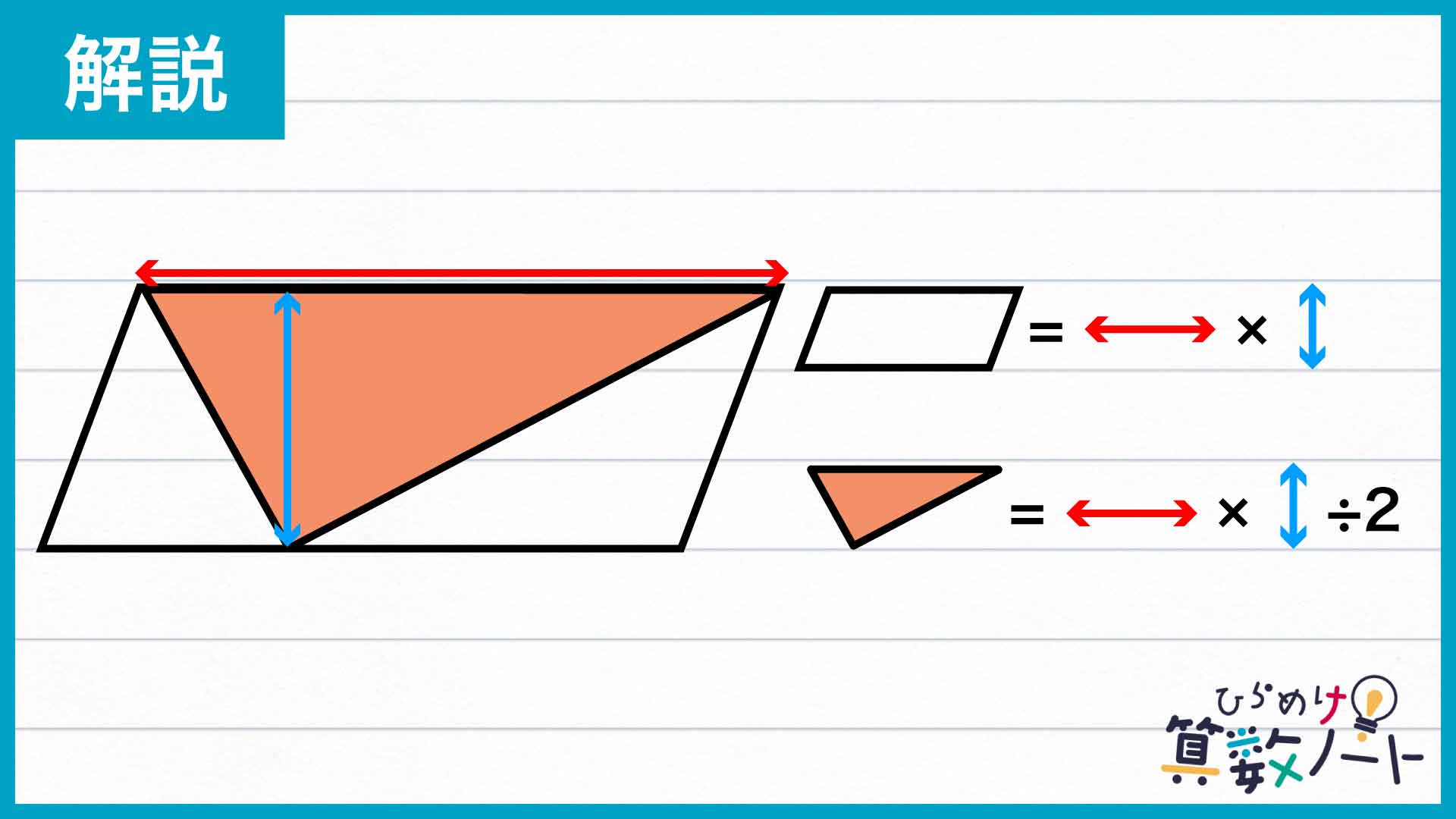
そして、小さい平行四辺形のうち上側のものに注目してみましょう。この平行四辺形は、中にすっぽり収まっている面積15の三角形と底辺の長さおよび高さが共通しています。
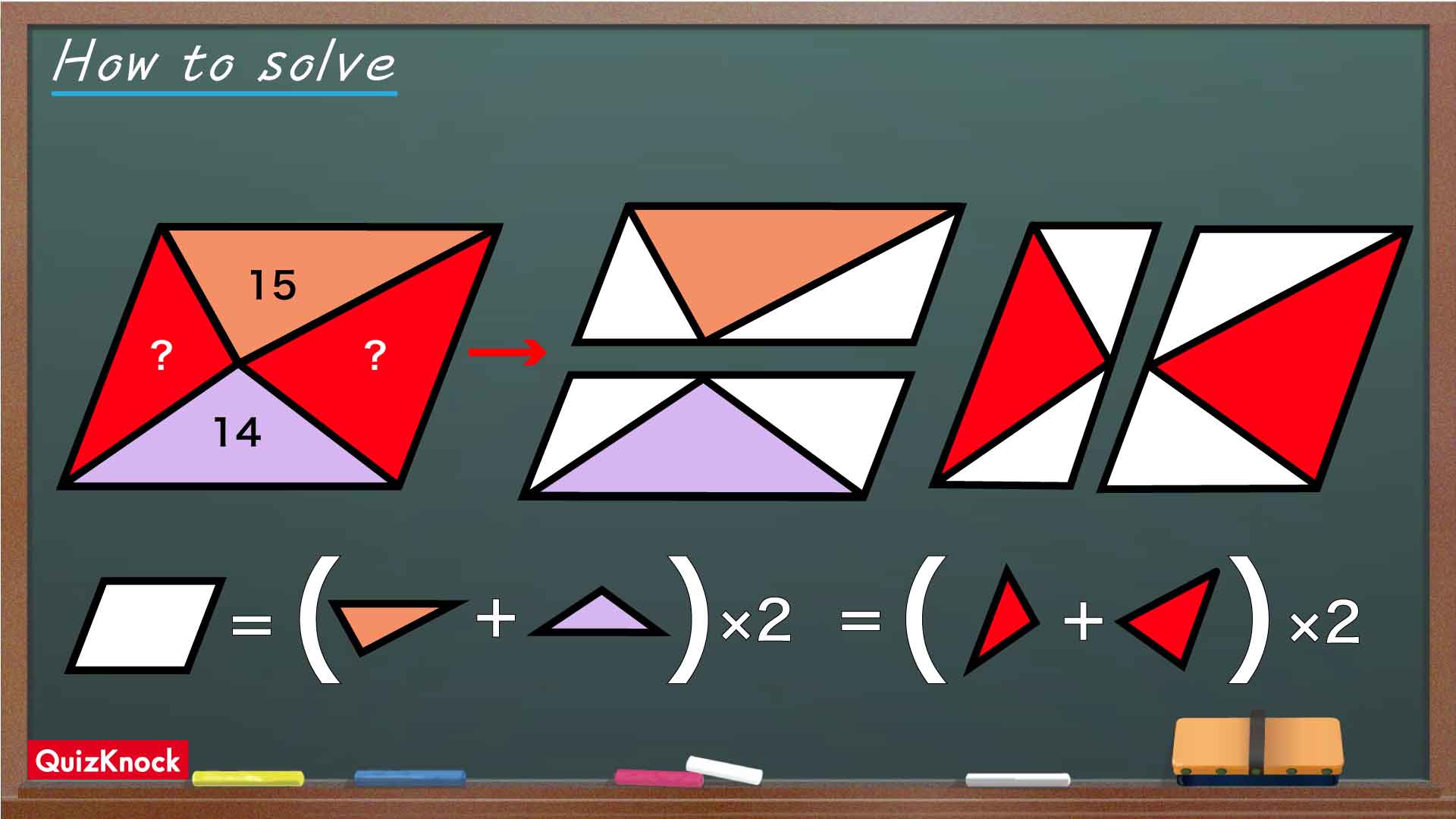
平行四辺形の面積は(底辺)×(高さ)、三角形の面積は(底辺)×(高さ)÷2という公式で求めることができるため、下の図において平行四辺形の面積は三角形の面積のちょうど2倍ということがわかるのです。
同様の関係が、下側の平行四辺形と面積14の三角形についてもいえます。したがって、面積15と14の三角形を合わせた面積が、大きな平行四辺形全体の面積のちょうど半分であるということがわかります。
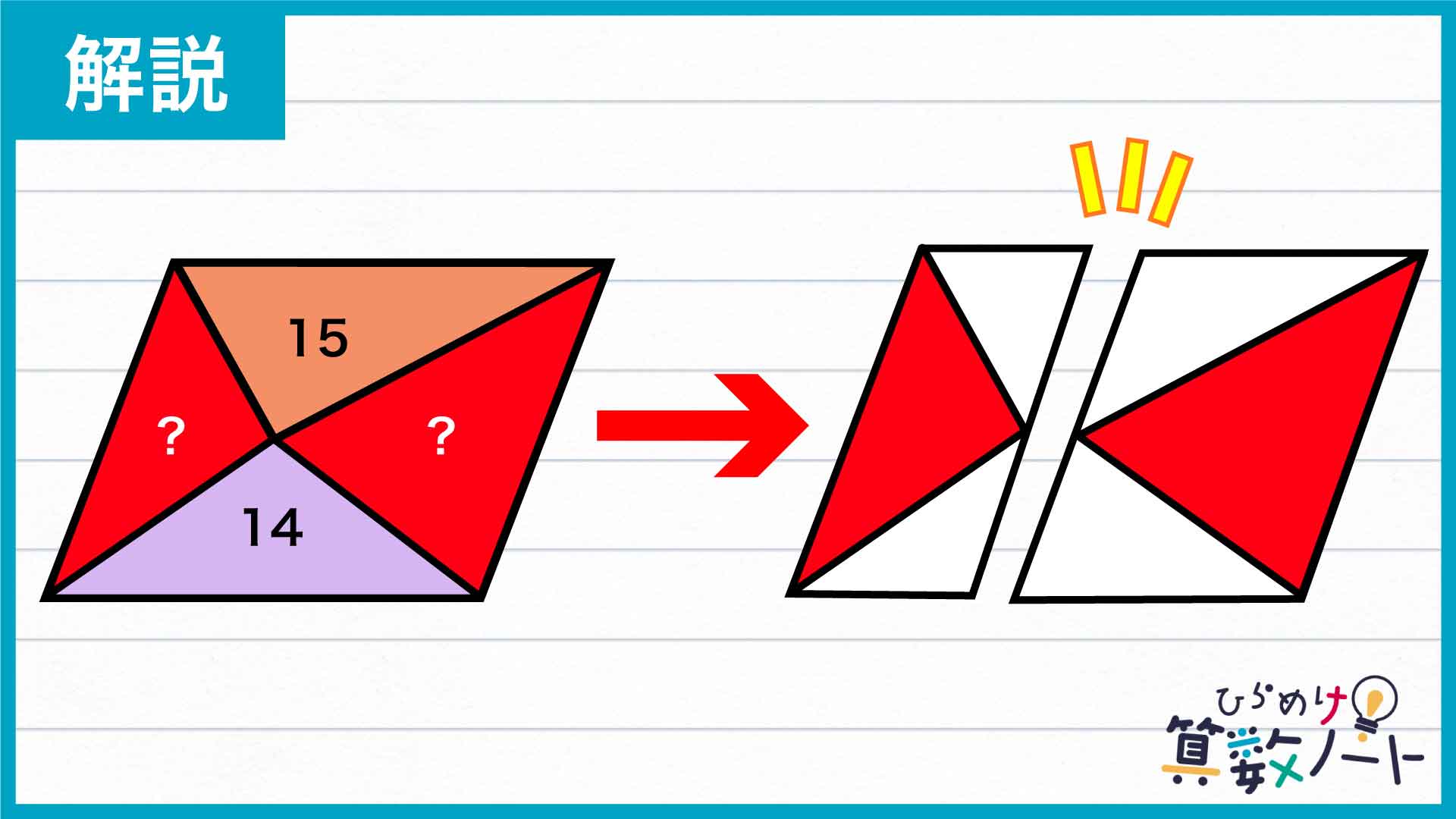
今度は、平行四辺形を左右に分割してみましょう。赤い2つの三角形がそれぞれ平行四辺形にすっぽり収まるように分けてみます。
すると、先ほどと同様に、三角形の面積の合計が大きな平行四辺形の面積の半分であるとわかります。
以上のことから、大きな平行四辺形を分割してできた4つの三角形のうち、上下・左右で向かい合う2つの面積の合計が互いに等しくなるのです。
したがって、赤い2つの三角形の面積の合計は15+14=29であるとわかります。
答え:29
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】










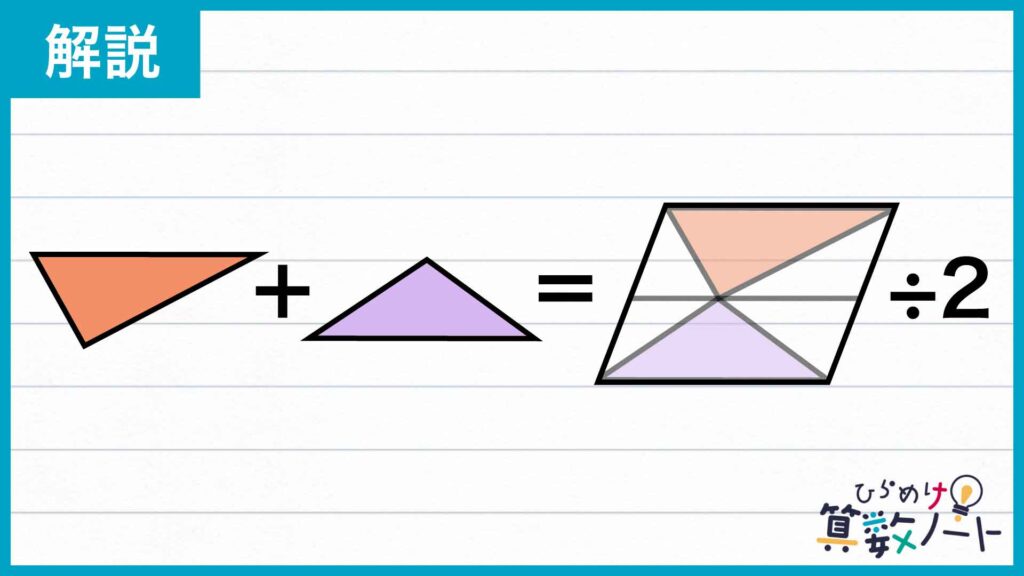

.jpg)









.jpg)






