解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
この問題の解き方をまとめた図がこちらです。
ポイントは、大きさが等しい三角形のペアを2つ見つけて、各部分の面積に成り立つ関係を考えることです。
では、このポイントを踏まえつつ解いていきましょう!
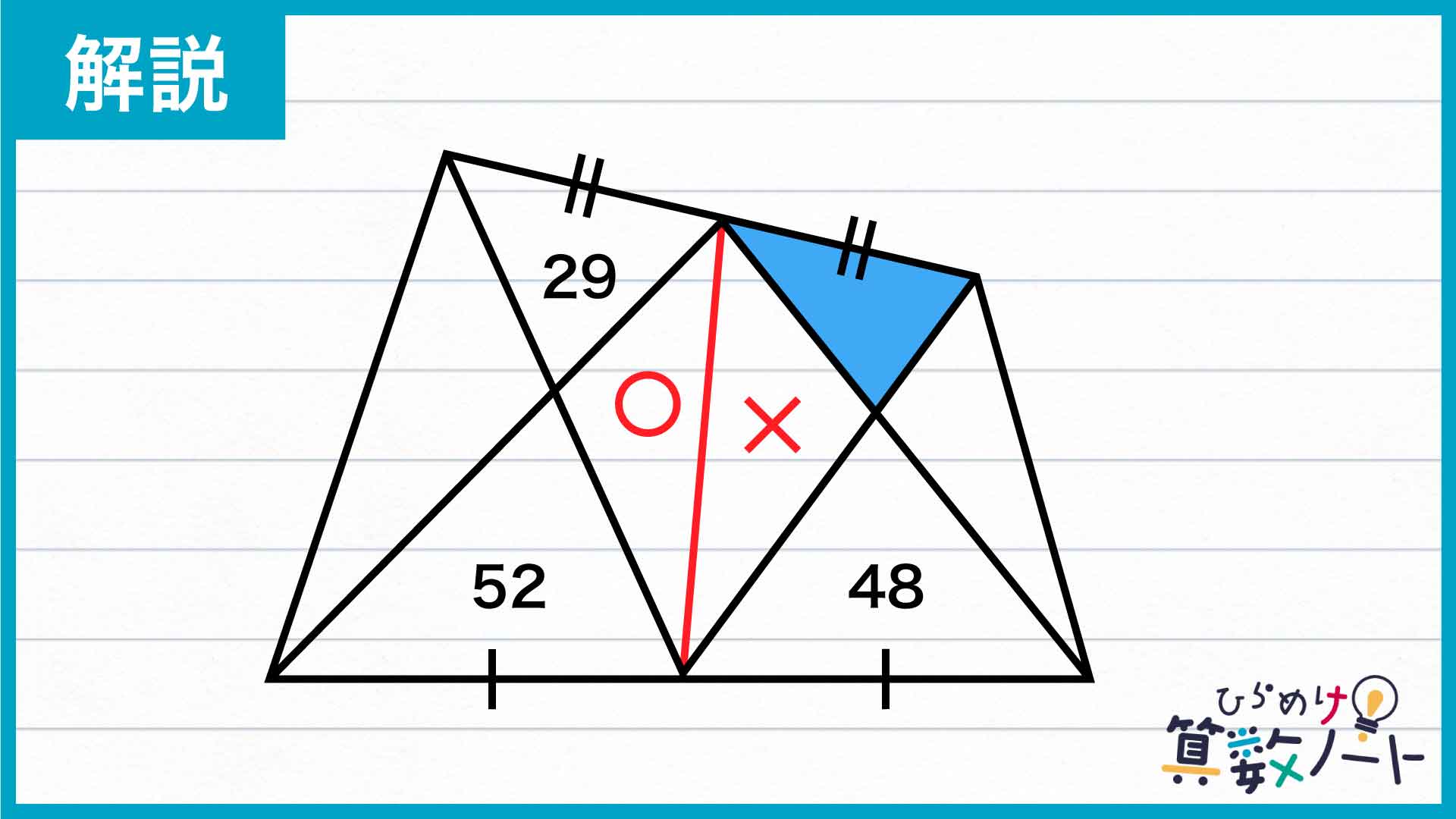
補助線を引いて、三角形のペアを見つける
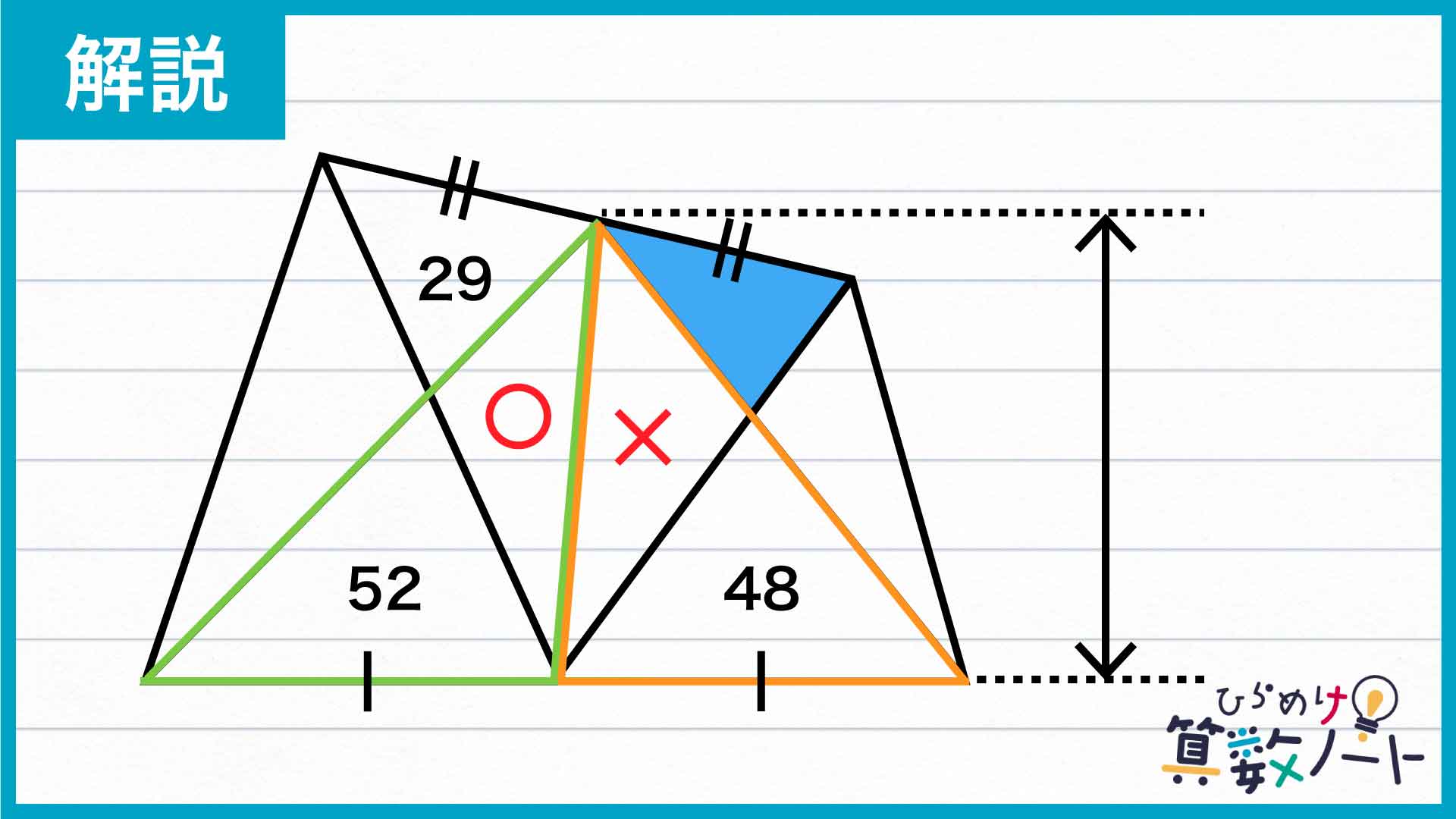
最初のポイントになるのは、真ん中にある四角形の部分をうまく補助線で区切ることです。辺を2等分している点を活かすため、図のように補助線を引いてみましょう。新しく生まれた2つの三角形の面積をそれぞれ〇、×とします。
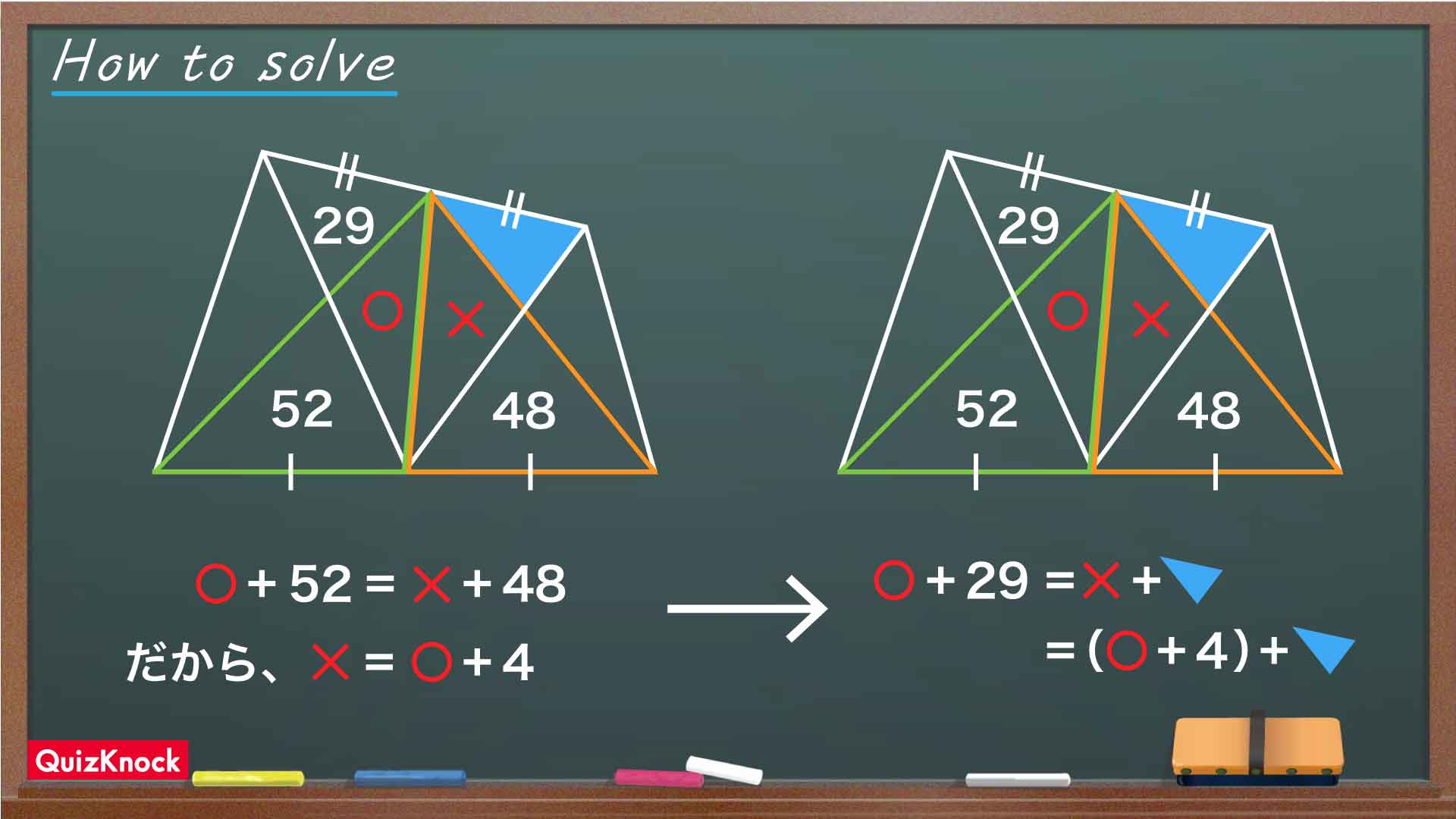
まず注目するのは、下の図において緑とオレンジで囲んだ2つの三角形です。
2つの三角形は底辺の長さが等しく、高さも共通しています。したがって面積が等しいことから、〇+52=×+48が成り立つとわかります。52-48=4なので、2つの三角形の面積が等しくなるには×が〇より4大きくなければなりません。
次に、下の図において緑とオレンジで囲んだ三角形のペアに注目してみましょう。
2つの三角形は、やはり底辺の長さと高さが等しくなっています。したがって面積も等しく、〇+29=×+青く塗りつぶされた部分が成り立ちます。先ほど求めた通り×は〇より4大きいので、〇+29=〇+4+青く塗りつぶされた部分となり青く塗りつぶされた部分は29より4小さいことがわかります。したがって、求める面積は29-4=25となります。
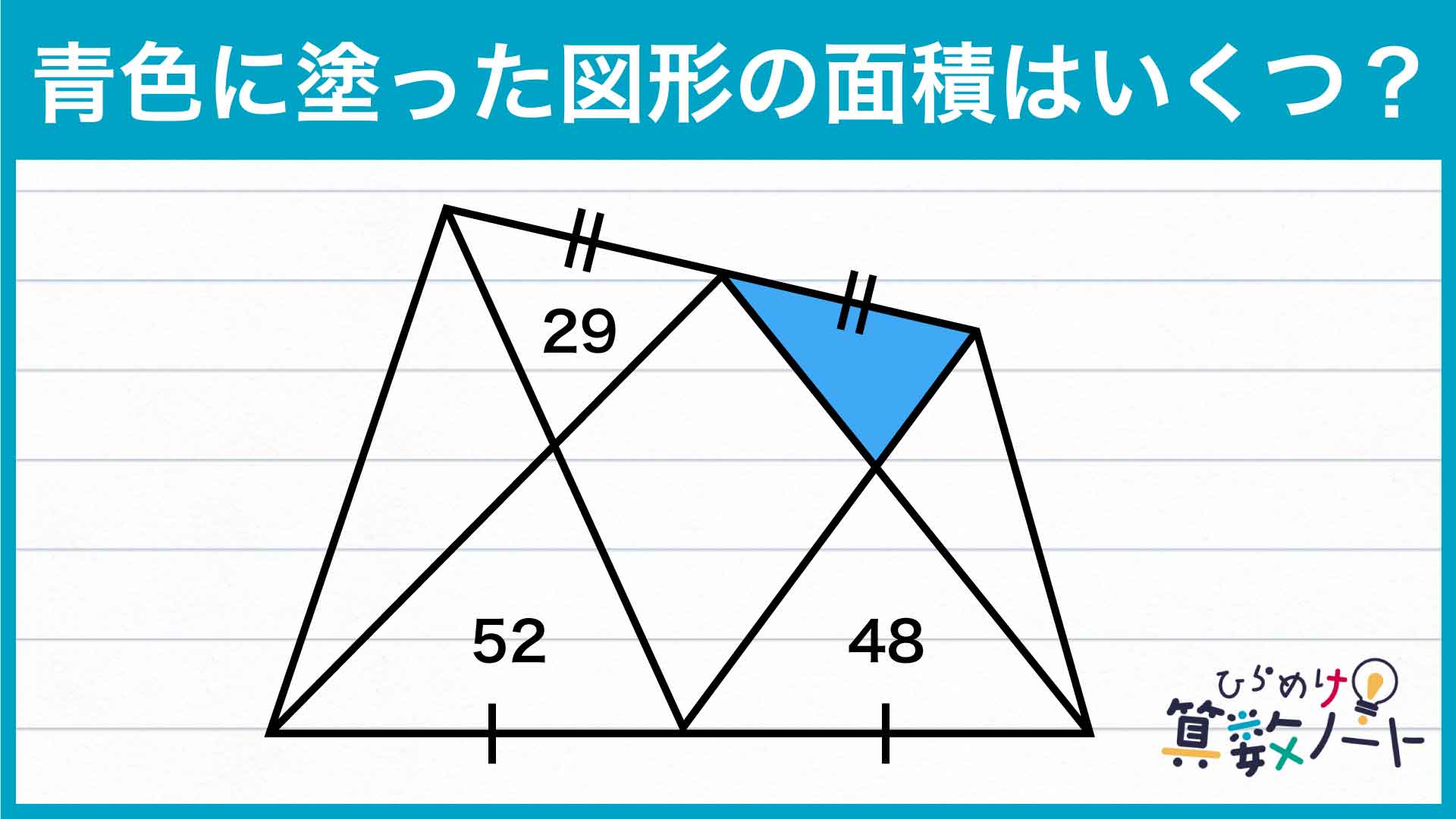
答え:25
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)









.jpg)







