ステップ2:分割してできた三角形の面積を求める
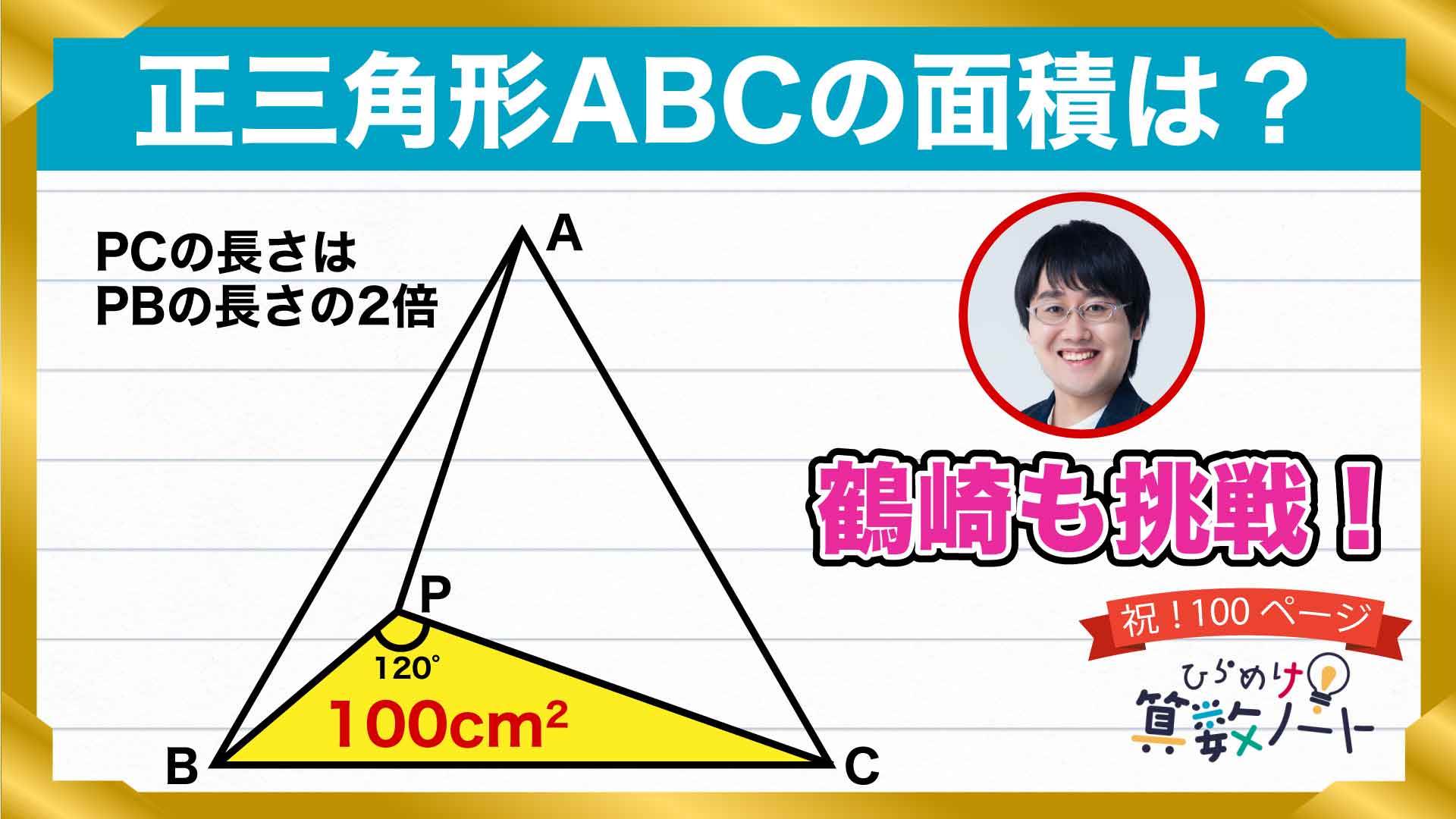
ステップ1までで、正三角形ABCを100cm2の三角形3つと、正三角形PQRに分割しました。ここからは正三角形PQRの面積を求めていきます。
ここからしばらくは、三角形APCの部分についてのみ考えます。
底辺の長さが等しく、高さが同じ三角形の組を見つける
三角形APCの中には、同じ長さの線分がいくつもあります。これらを駆使すると、複数の三角形の面積比がわかります。
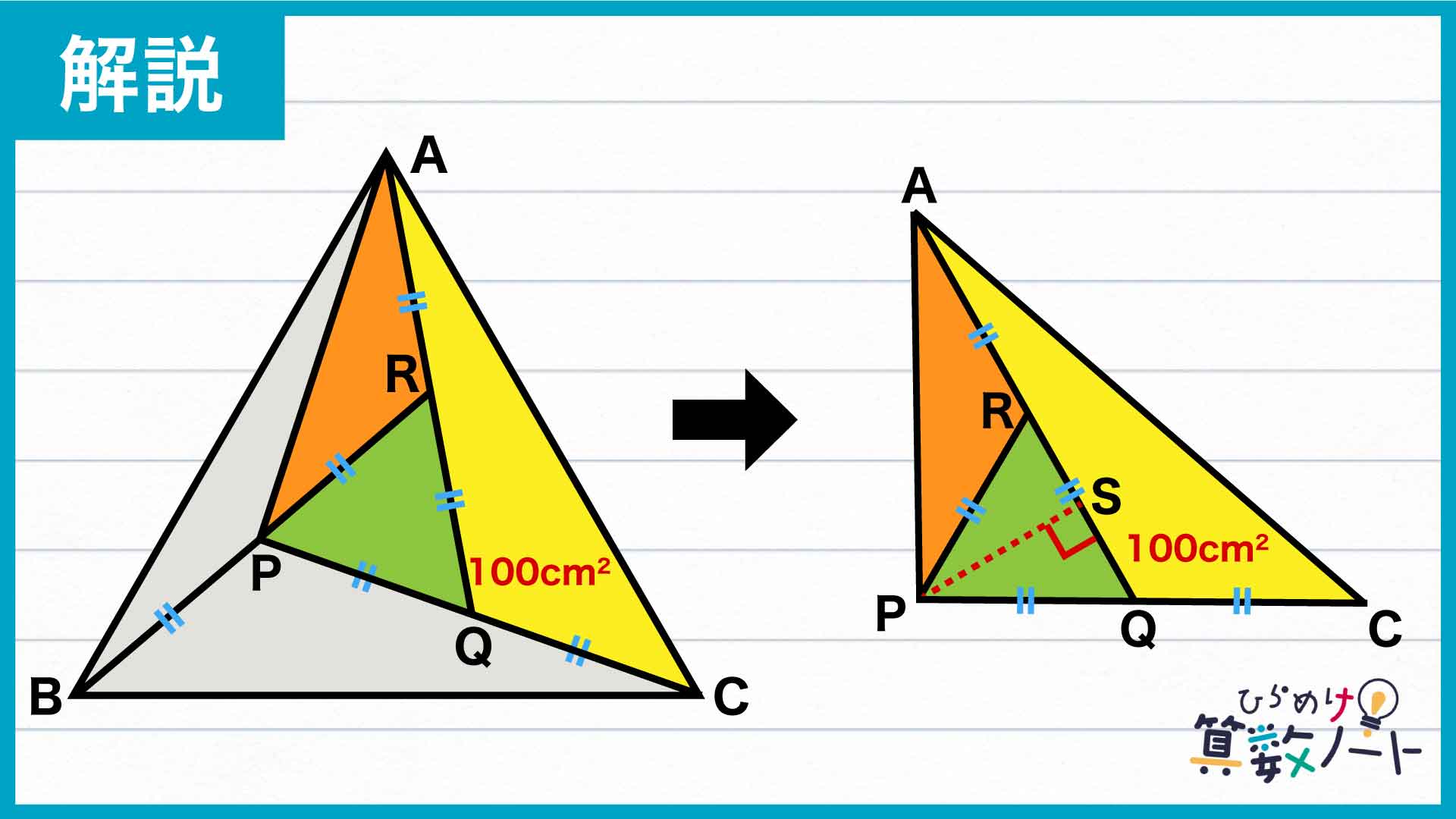
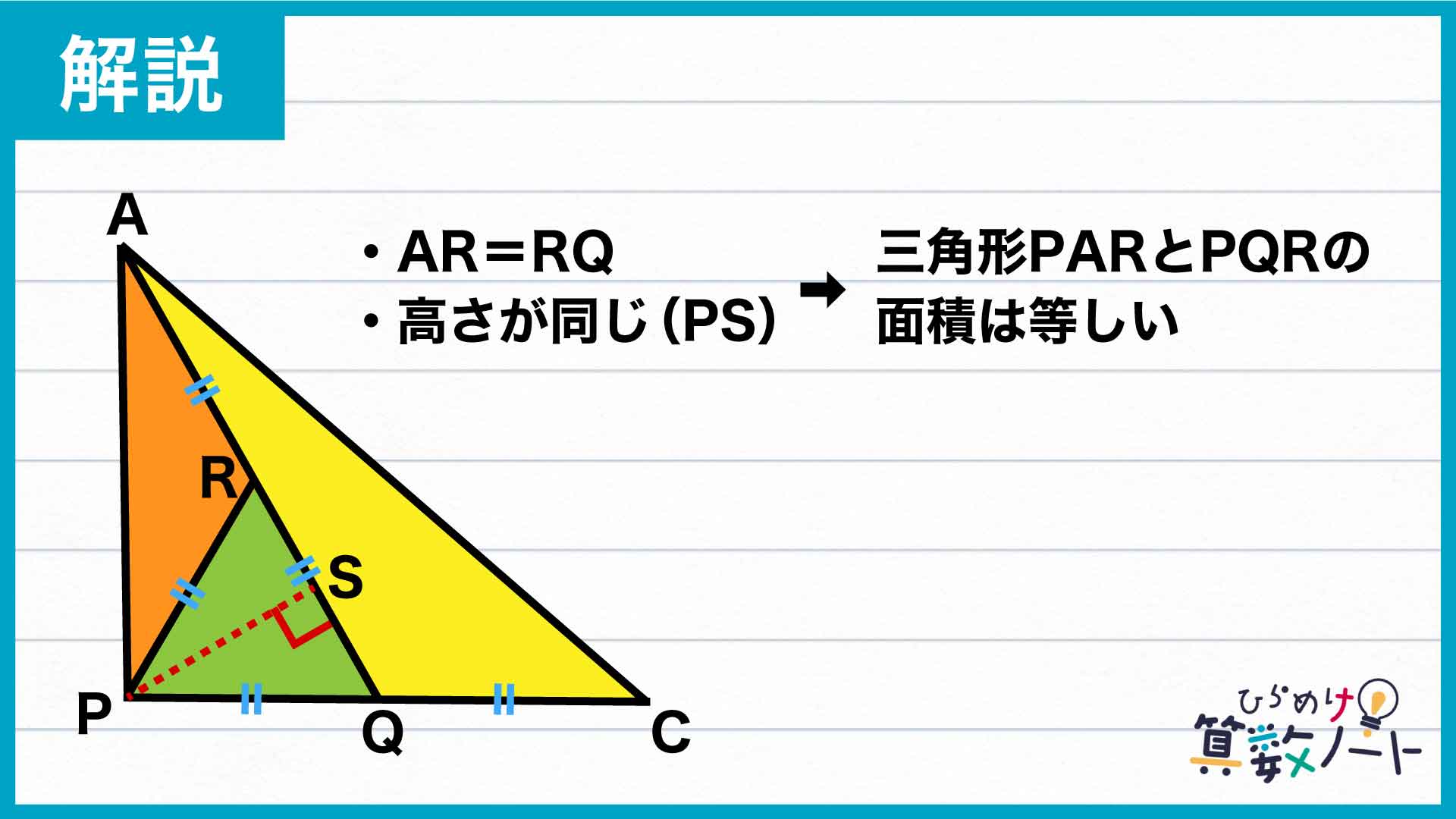
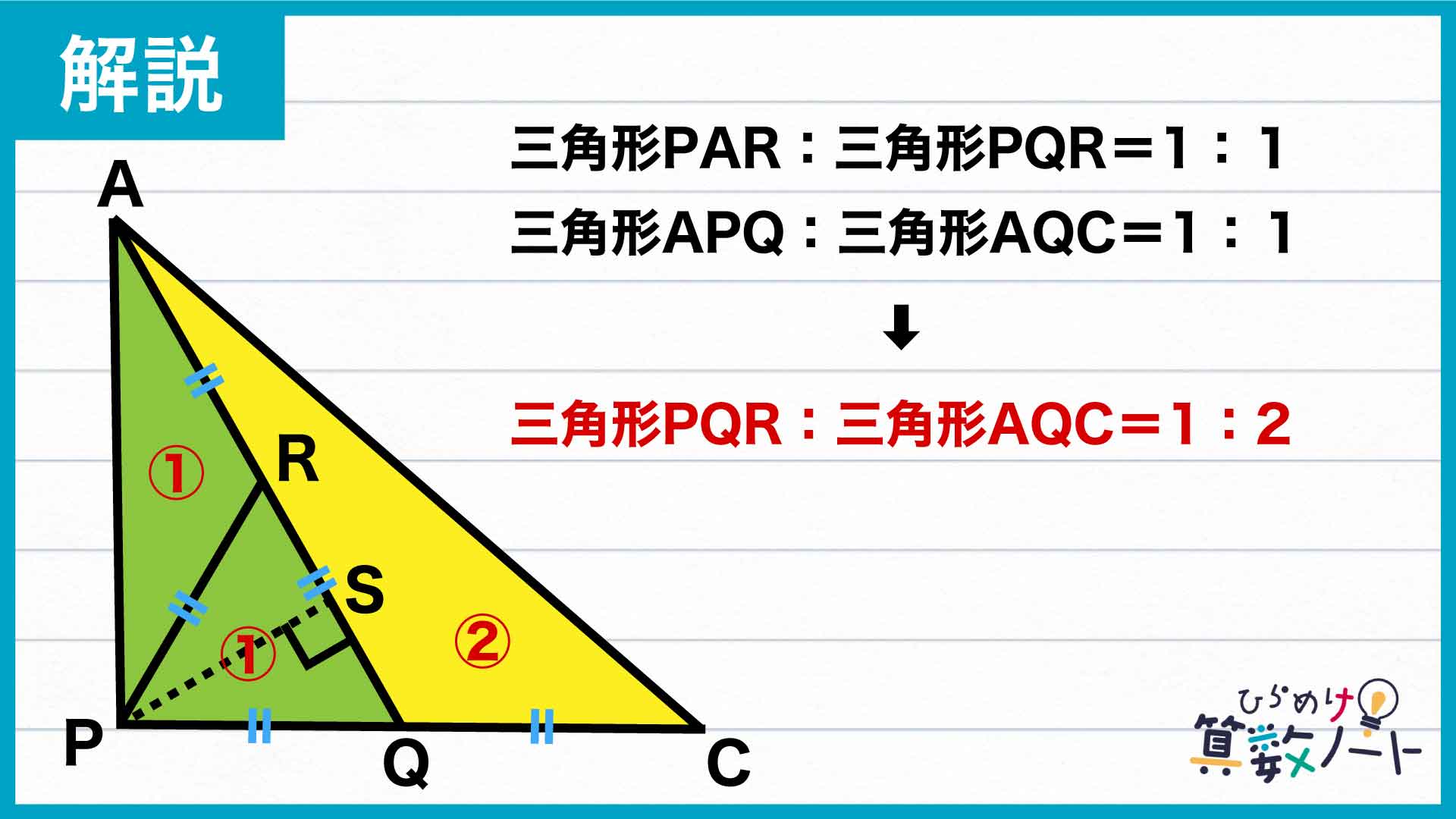
まずは、三角形APQを構成する三角形PARとPQRについて。PからAQに向かってAQと垂直な線PSを引くと、AQを底辺として見たとき、ARとRQの長さが等しく、どちらも高さは線分PSとなっています。
ここで、三角形の底辺の長さと高さ、面積について成り立つ以下の関係性を使います。
この関係を使うと、三角形PARとPQRの面積は等しいことがわかります。
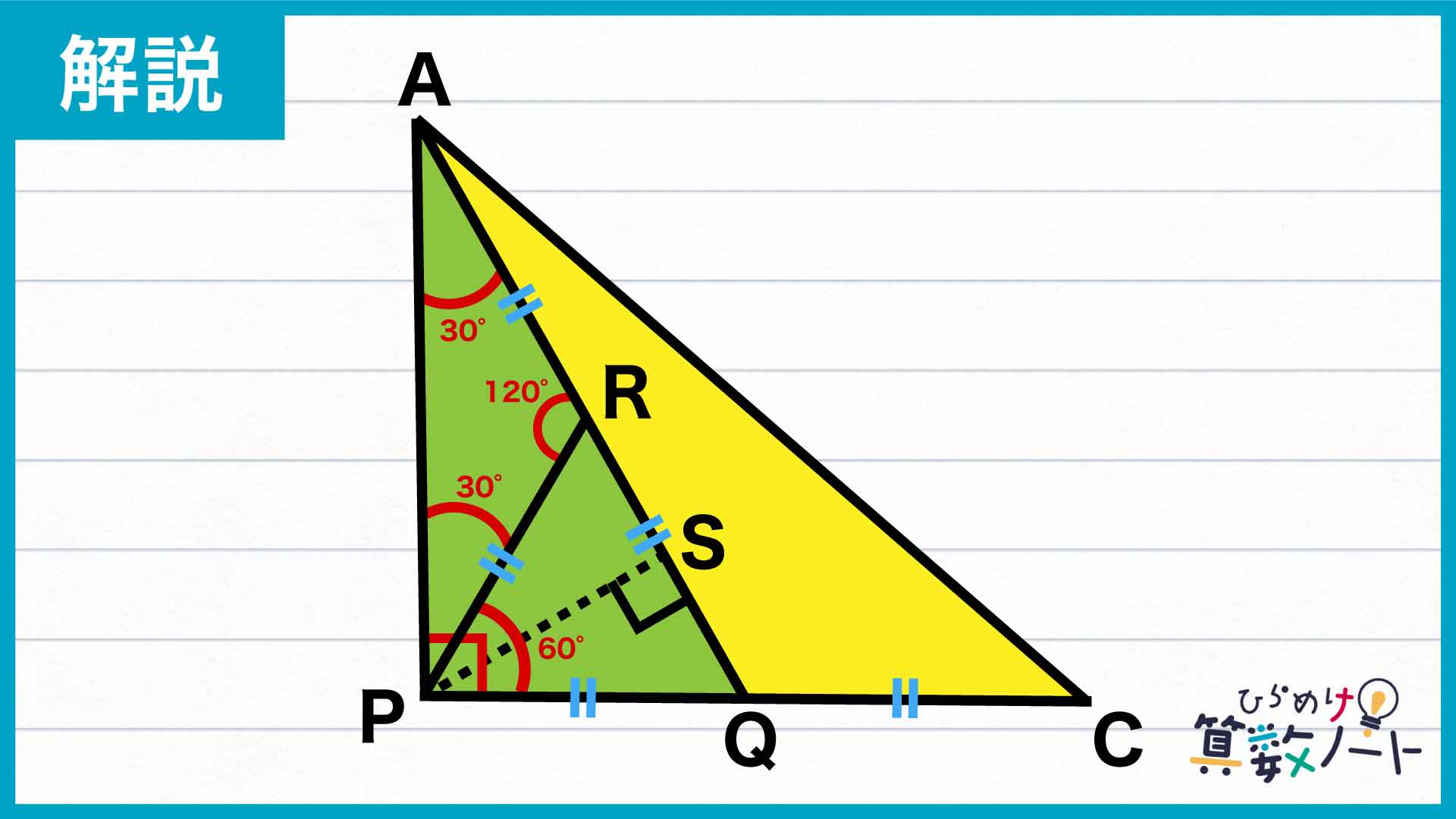
次に、三角形APCを構成する三角形APQとAQCについて。PCを底辺としてみると、PQとQCの長さが等しくなっています。
また高さについては、三角形PQRが正三角形であること、および三角形RAPが二等辺三角形であることから角APCの大きさは90度と求められ、三角形APCが直角三角形、すなわちAPが高さにあたることがわかります。
したがって先ほどのhow to solveで示した関係を使うと、三角形APQとAQCの面積は等しくなります。
以上をふまえると、三角形PARと三角形PQRの面積比が1:1で、それらを足し合わせてできる三角形APQと三角形AQCの面積比が1:1なので、三角形AQCの面積は、三角形PQRの面積の2倍であることがわかります。
そして、三角形AQCの面積は100cm2であるとわかっているので、正三角形PQRの面積は、その半分の50cm2です。
あとは足し合わせるだけ!
ステップ2の冒頭で、正三角形ABCは100cm2の三角形3つと、正三角形PQRで構成されていると説明しました。正三角形PQRの面積は50cm2なので、正三角形ABCの面積は、100×3+50=350cm2となります。
答え:350cm2
おまけ
今回出題した問題を、東大の大学院で博士号(数理科学)を取得した鶴崎に解いてもらいました。























.jpg)






