解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
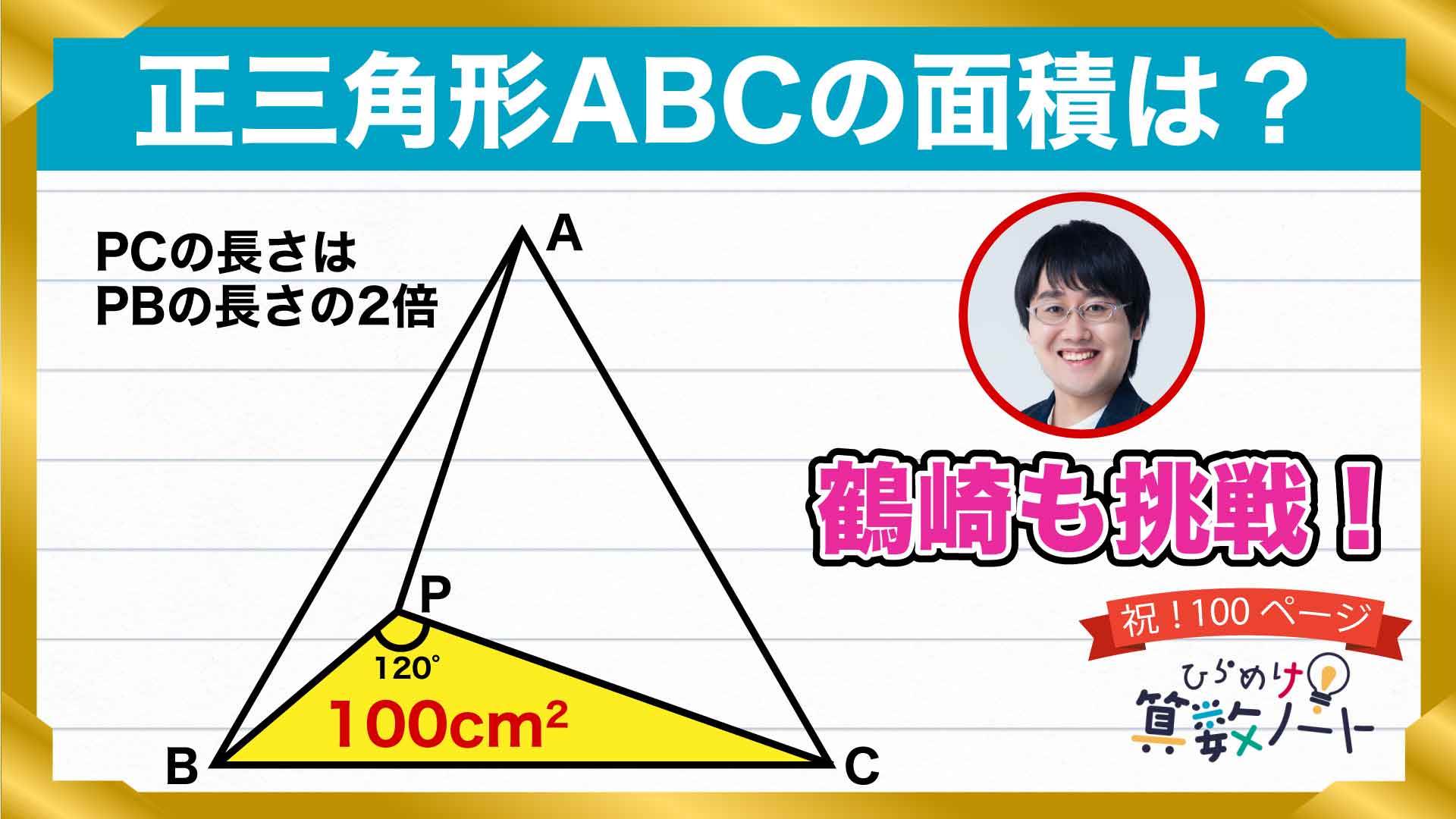
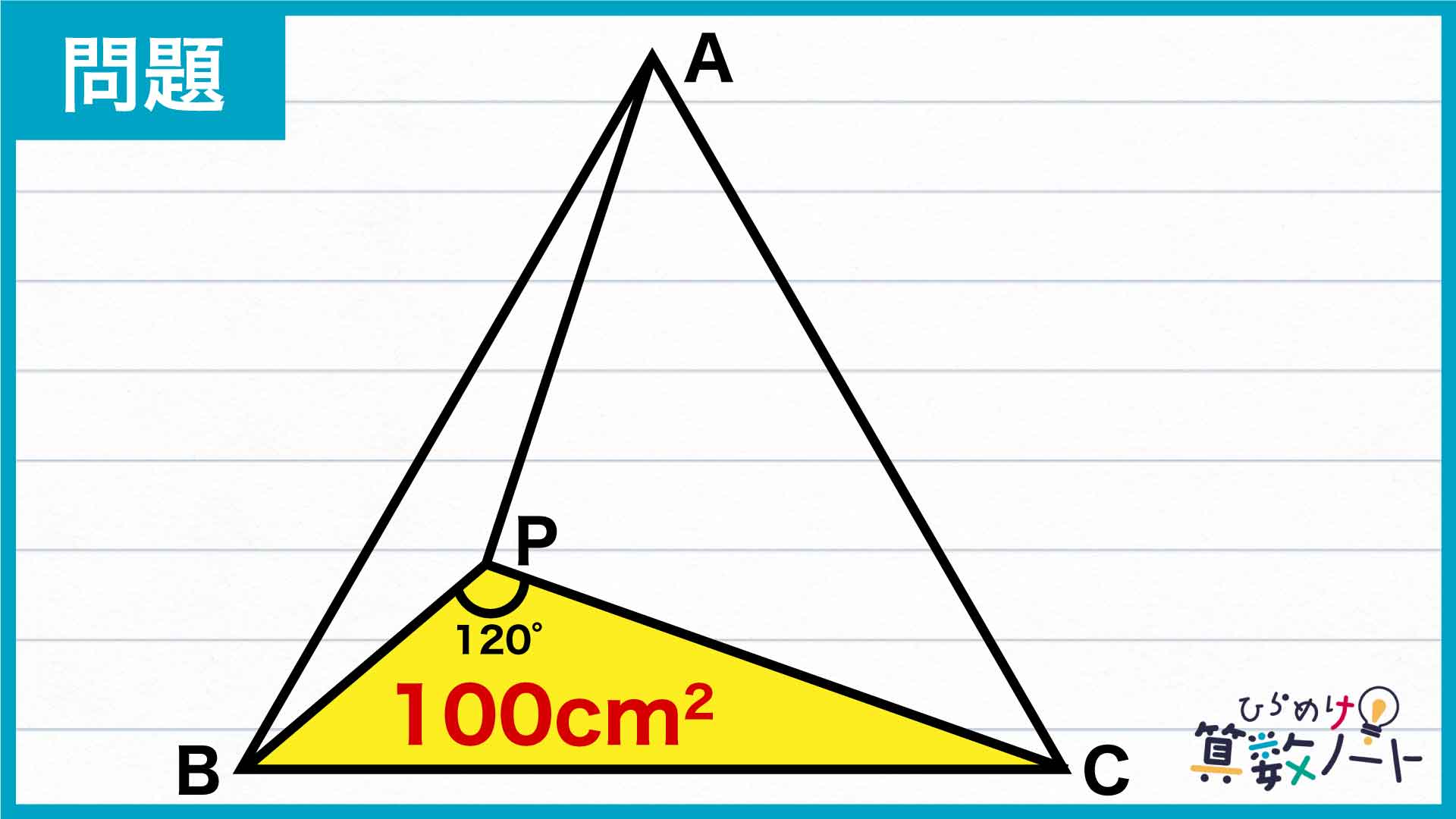
与えられている情報があまりにも少ないので、このままの状態では答えを導くことができません。ポイントは、以下の2つのステップを経ること。面積を求める前に、まずは正三角形ABCを分割することから始めます。
上記のポイントをふまえ、早速解いていきましょう!
問題を解くための2つのステップ
ステップ1:正三角形ABCを分割する
1本目の補助線と合同な三角形
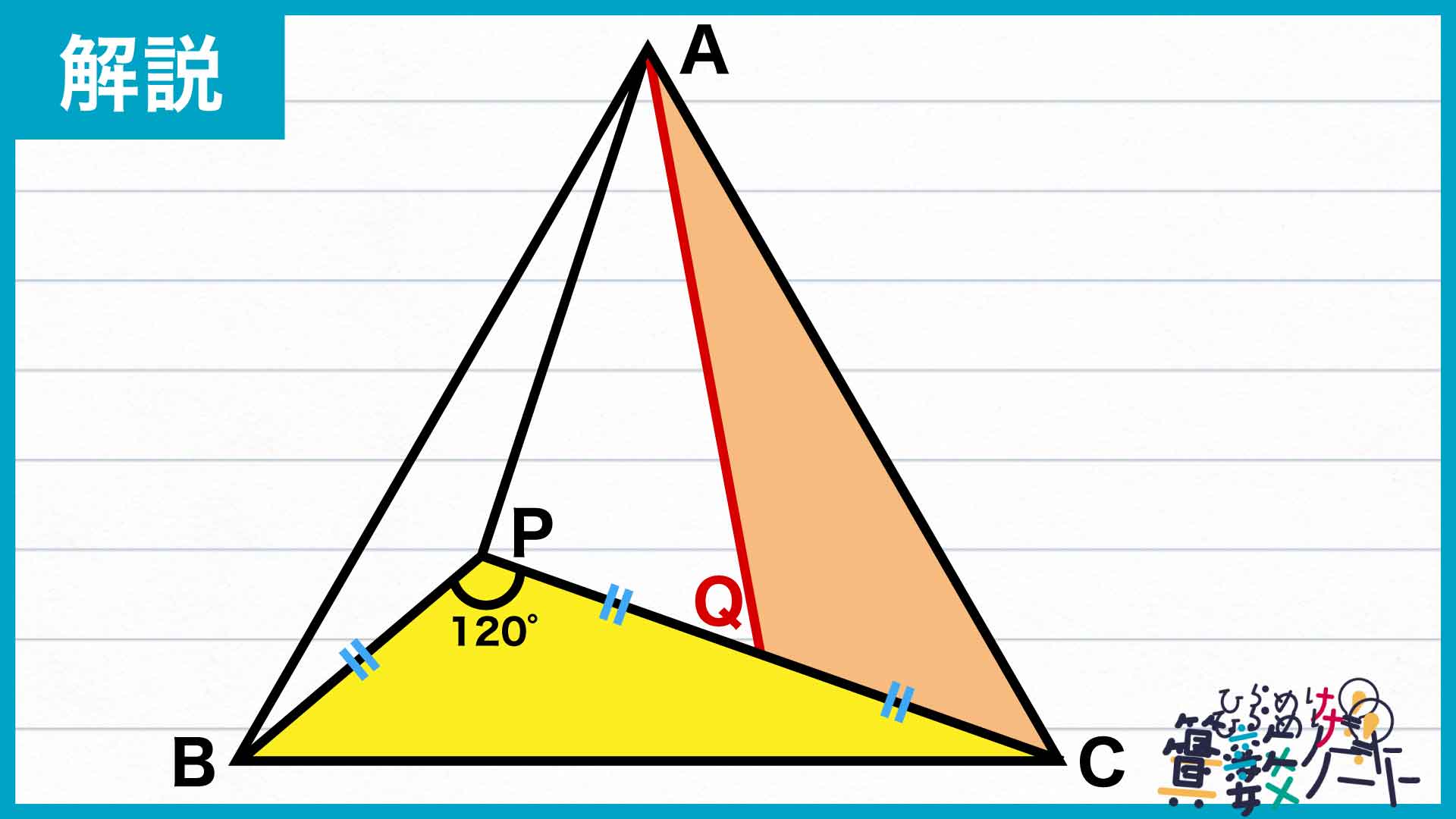
まず手始めに、補助線を1本引きます。この補助線がなかなかの曲者です。
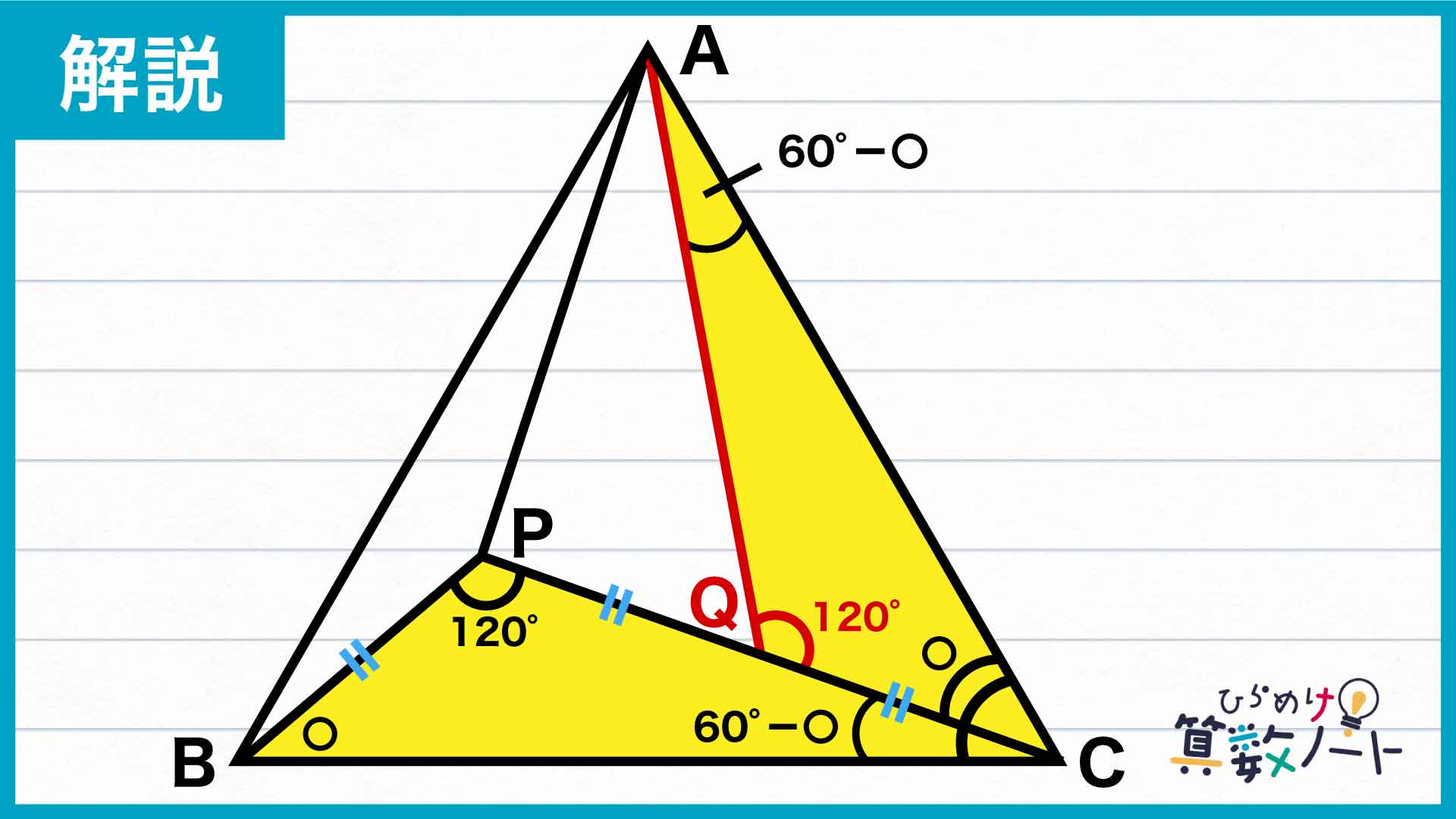
どう引くかというと、線分PCの中点をQとし、AとQを結びます。このとき、線分PCの長さがPBの長さの2倍であることから、3つの線分PB、PQ、QCはすべて同じ長さになります。
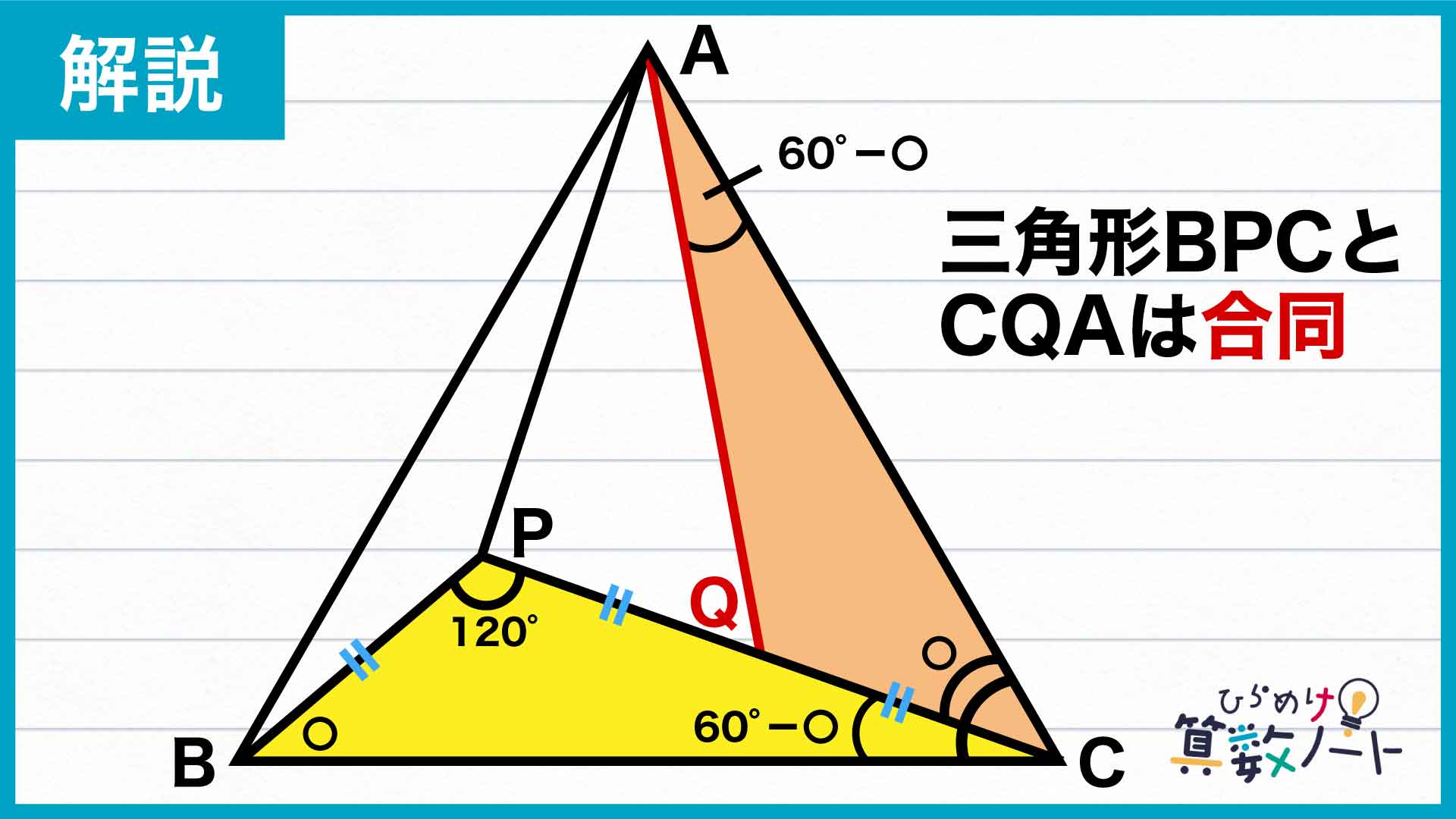
ここで、2つの三角形BPCとCQAに着目します。角PBCの大きさを〇とおくと、三角形の内角の和が180度であることと、角BPCの大きさが120度であることから、角PCBの大きさは180-(〇+120)=(60-〇)と表されます。また三角形ABCは正三角形なので角ACBの大きさは60度であり、角QCAの大きさは60-(60-〇)=〇となります。したがって、角CBP=角ACQです。
さらに、三角形ABCが正三角形であることからCB=AC、またPB=QCと合わせると、三角形BPCとCQAは2つの辺の長さと、それらに挟まれた角の大きさがそれぞれ等しく、合同であることがわかります。
合同な三角形は対応する角の大きさが等しくなるので、角CQAの大きさは、角BPCの大きさと同じ120度になります。
2本目の補助線と正三角形
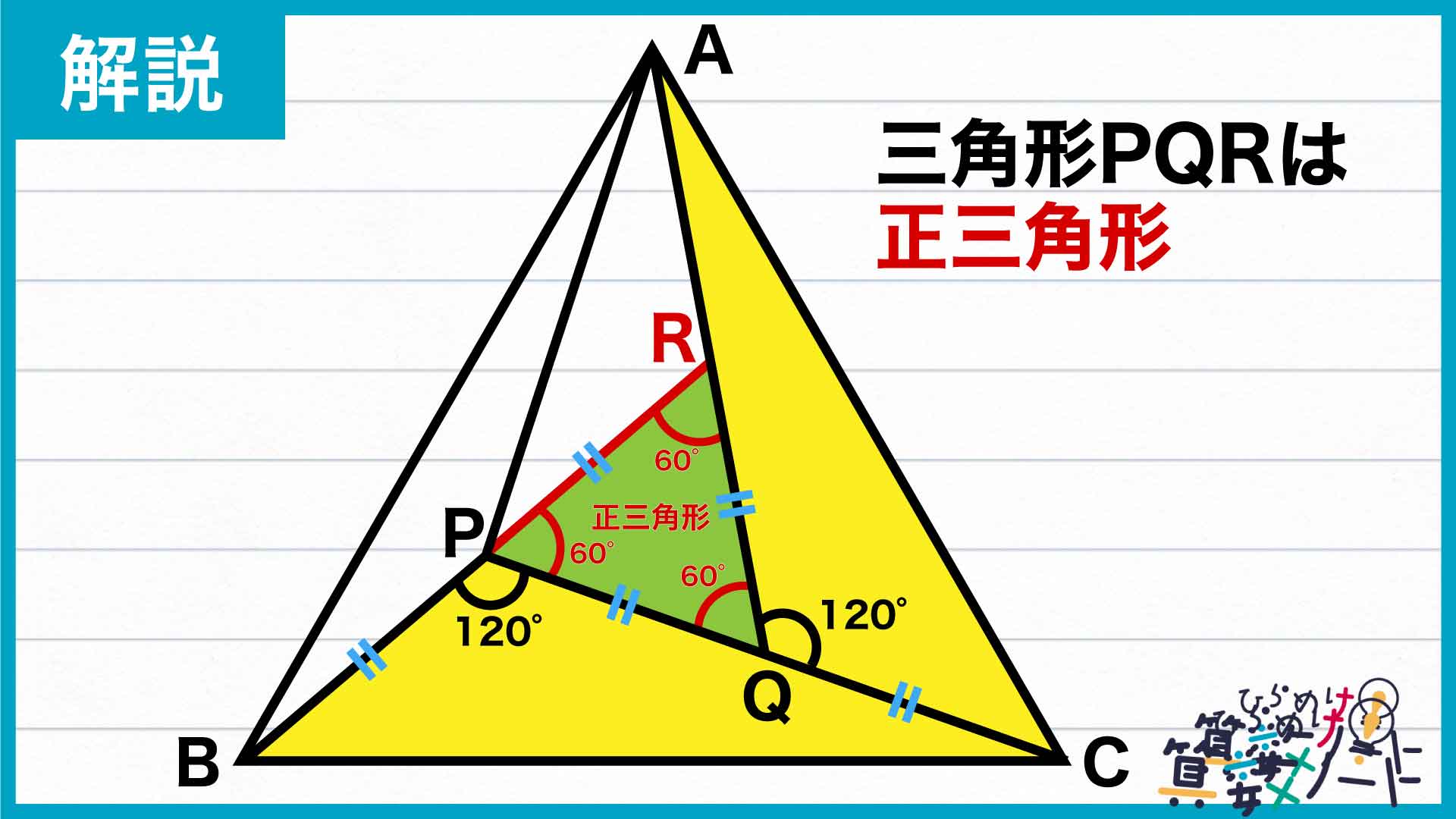
次に、補助線をもう1本引きます。線分BPを延長し、線分AQとの交点をRとすると、真ん中に三角形PQRができます。
この三角形PQRについて見てみると、角BPC、角CQAの大きさが120度であることから角RPQ、角RQPの大きさは60度となり、角PRQの大きさも60度になります。したがって三角形PQRは正三角形であることがわかります。
正三角形ABCは、どんな三角形でできている?
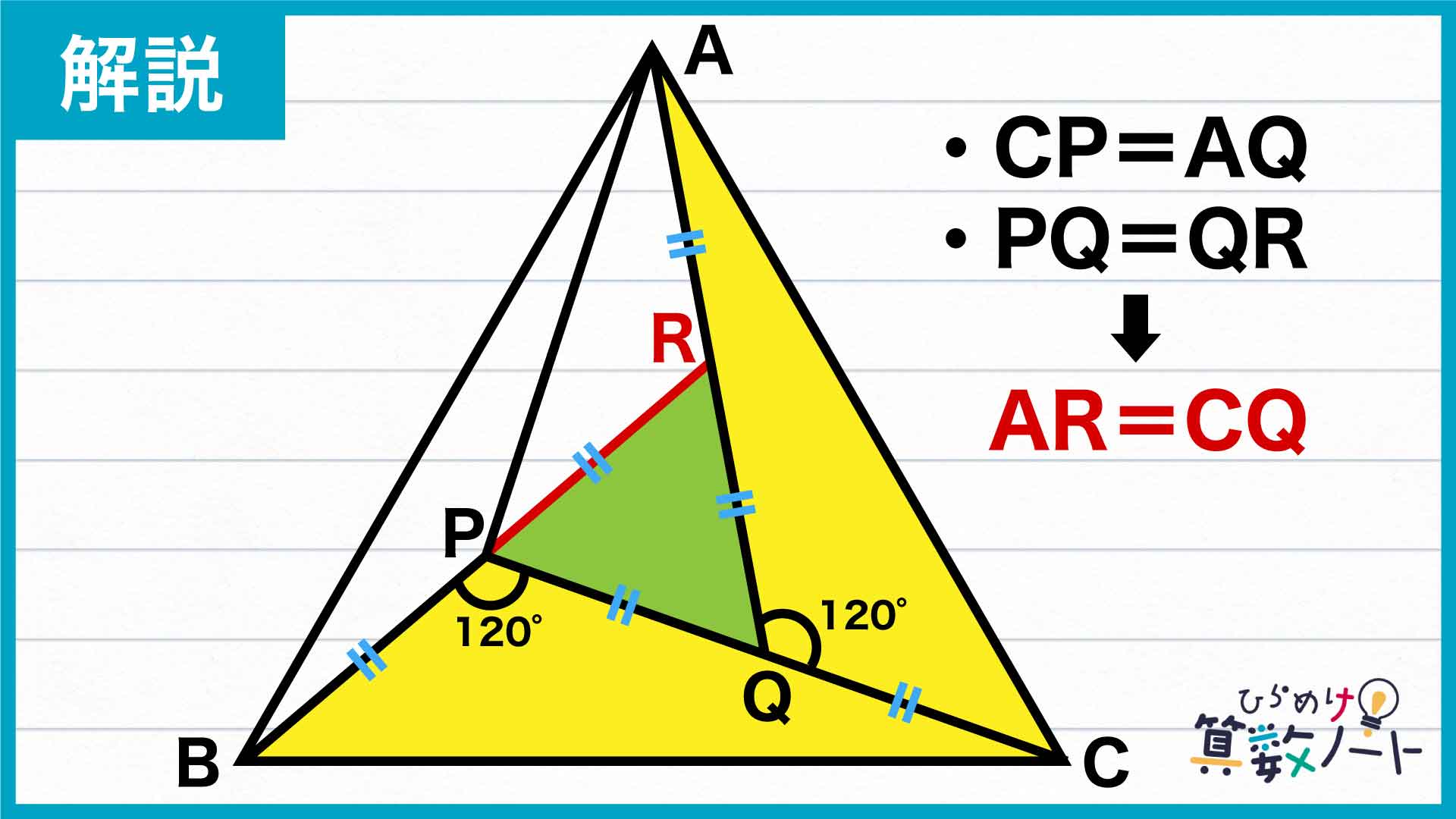
三角形BPCとCQAが合同であることからCP=AQであること、そして三角形PQRが正三角形であることからPQ=QRであることをふまえると、AR=CQが成り立ちます。したがって、6つの線分AR、RQ、BP、PR、CQ、QPはすべて同じ長さになり、それらを2つずつ足し合わせた3つの線分AQ、BR、CPも同じ長さになります。
そして2つの三角形CQAとARBに着目すると、
- CA=AB(三角形ABCが正三角形)
- QC=RA
- AQ=BR
が成り立っており、3辺の長さがすべて互いに等しいのでこの2つの三角形は合同です。
以上より正三角形ABCは、3つの合同な三角形BPC、CQA、ARBと、正三角形PQRでできていることがわかりました。問題より、3つの合同な三角形の面積はそれぞれ100cm2であることがわかっているので、正三角形PQRの面積さえ求めることができれば、答えを出すことができます。























.jpg)






