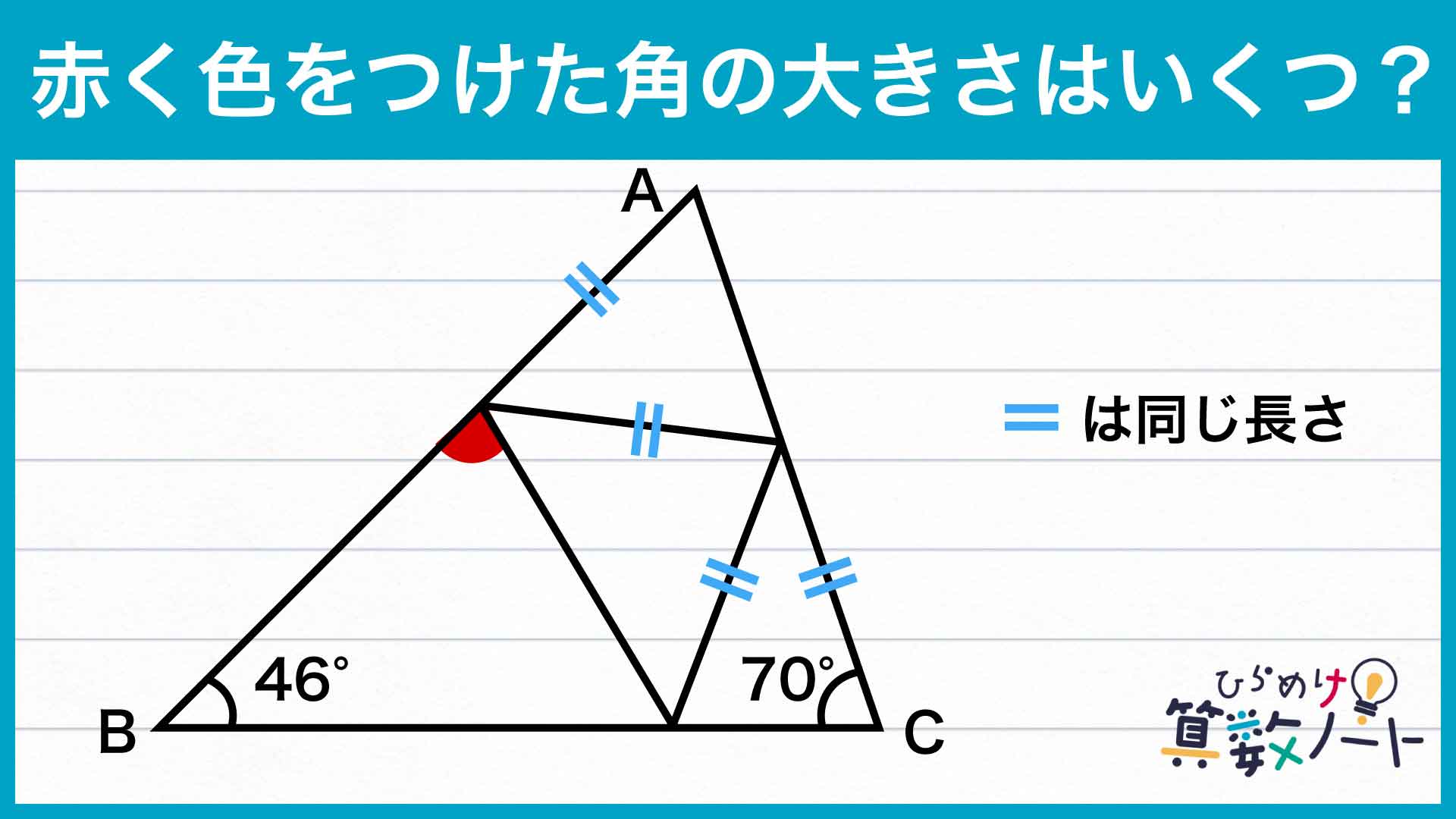
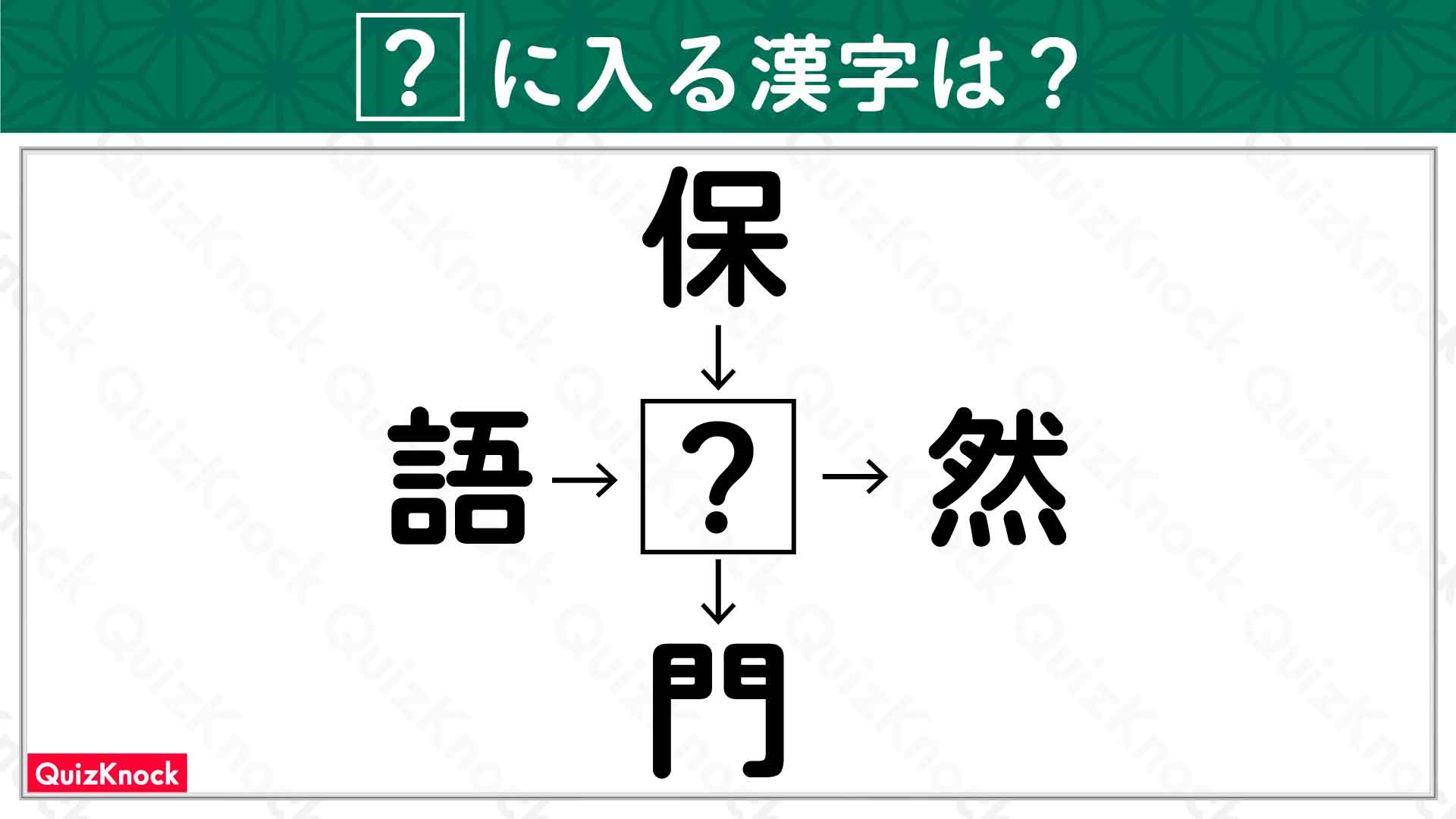
ポー。コジマです。
マイケル・ジャクソンの代名詞とも言える「ゼロ・グラビティ」は、身体を一直線に伸ばしたまま前に傾けるパフォーマンスだ。
自分でやってみれば分かるが、タネもシカケもないままこれをやろうとすると10°も倒せずによろけてしまう。マイケルは、靴に金具を取り付けて床と固定することで何とかゼロ・グラビティを実現しているのである。
では、そんな金具がない場所でゼロ・グラビティを披露するにはどうしたらよいか。身体を前に倒すには、身体の前で体重を支えてくれる何かが必要だ。
何か……そうだ、風だ!
超強力な扇風機の風を前から浴びれば、その圧力(抗力)が身体を支えてくれるかもしれない。どの程度の風速が必要か計算してみると、台風くらいの風速があればいける!
45°の前傾姿勢を維持する力を求める
前提として、扇風機は人間に向かうように少し斜め上向きに置くことにする(風は身体の真正面で受けるときに最も抗力が大きくなるので)。
まず、ゼロ・グラビティを風で支えている人にかかっている力を図示してみる。
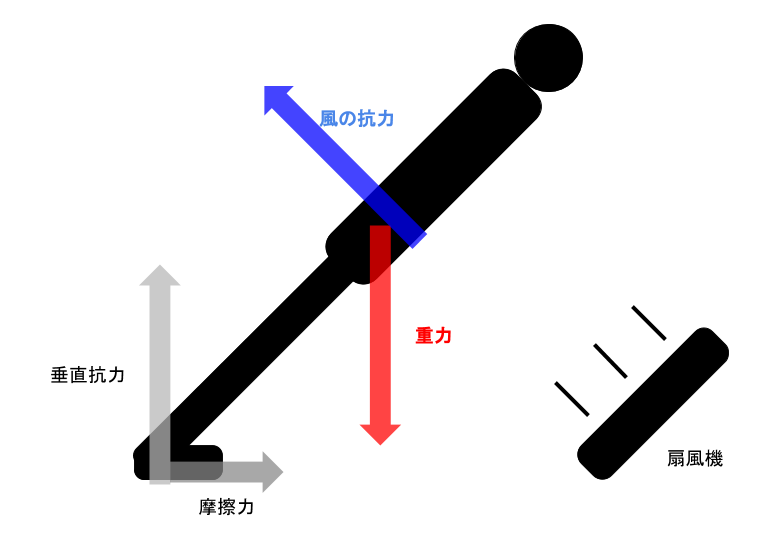
身体の回転が釣り合うとき、重力のトルクの大きさ=抗力のトルクの大きさが成立する。トルクは物体を回転させる働きのことで、支点からの距離×力で求められる。詳しくはこちらの記事で。
人間の重心までの距離をrとすると、支点から重力の矢印までの距離はrcosθ。重力はmg(m: 体重、g: 重力加速度)なので、トルクの大きさはmgrcosθとなる。

一方、抗力の大きさをDとすれば、抗力のトルクの大きさはDr。
この2つが等しくなるのだから、Dr=mgrcosθで、D=mgcosθとなる。
よって、体重m=70kgの人が身体をθ=45°傾けるのに必要な抗力の大きさは、重力加速度g=9.8として70×9.8×cos45°=485N(ニュートン)。
485Nって風速ではいくら?
では、485Nの抗力をもたらす風の速さは?あくまでも概算にはなってしまうが求めてみよう。
抗力の大きさは次の式で求められる。

空気の密度は、1気圧・気温20℃なら約1.20kg/m3。
代表面積とは、風の方向から物体を見たときの面積。人間の代表面積を求めるのは難しいが、身長1.8m×肩幅0.45mの長方形の70%くらいと仮定して0.567m2としておく。
抗力係数は物体の形状により異なり、実験などに基づいて求める値だが、こちらによるとスキージャンパーの抗力係数は1.2〜1.3だという。ここでは1.25としよう。
上の抗力を求める式をVについて変形すると、
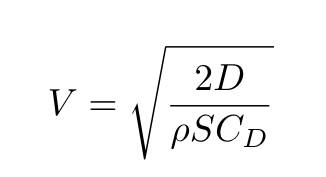
ここまでに求めてきた値をすべて代入すると、風速は33.8m/s!
日本の風力階級では、風速32.7m/s以上の風が最強の風力12に相当する。つまり風速33.8m/sは暴風中の暴風である……。
でも風速500m/sとかではないし、(これだけの風が起こせる扇風機が存在するかは別として)ギリギリ実現できそうな気がする……しない?









.jpg)