コジマです。
突然だが、今からヘンな話をする。どこがヘンなのか考えてみてほしい。
あるとき、ウサギとカメが鬼ごっこをすることになった。足の速いウサギが鬼になり、少し後ろのほうからカメを追いかけた。
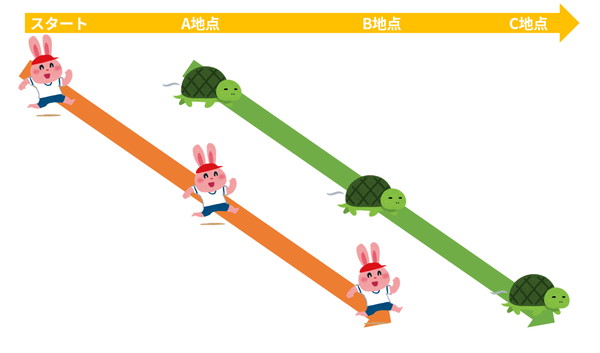
両者は同時にスタートした。ウサギがハンデ分の距離を走ってカメのスタート地点に着いた頃、カメはその少し先を走っている。そこをA地点としよう。
さらに少し経って、ウサギがA地点に着く頃には、カメはさらに先のB地点にいる。
ウサギがB地点まで来たときにはカメはさらに先のC地点まで到達しているし、ウサギがやっとC地点に着いたときにはカメは既にD地点にいて……。足が速いはずのウサギは永遠にカメに追いつけない。
エリック・ワイナイナは2分くらいのハンデを覆して赤坂5丁目ミニマラソンに勝つし、そんな訳がないのは直感的に分かるのだが、こう言われると確かに追いつけない気もしてくる。
実は、この話は古代ギリシアの哲学者・ゼノン(画像右の先生)が発した「アキレスと亀」という有名な逸話なのだが、いざ反論してみいと言われてパッと説明できるだろうか。
私がいくつか反論の仕方を伝授するので、今度ゼノンに会って話を吹っ掛けられたときにドヤ顔で論破しよう。
距離は縮まってるでしょ
上の話では「前のカメの位置に着いたときにはカメはさらに前にいる」という論調で話が展開されている。一見ごもっともな論理なのだが、実際にイメージすると追いつくタイミングが近づくにつれて「前のカメの位置に着いたとき」の時間的な間隔が短くなっていくことに気付くはず。
「A地点」にウサギがついた時、カメは5分前にそこを旅立っていた。次にウサギが「B地点」についたとき、カメは3分前にそこにいた……というふうに、カメがウサギより遅いならば、「カメがn分前にそこにいた」のnは、進むに連れて小さくなるはずなのだ。

なぜこれが見逃されがちなのかというと、「A地点とB地点」「B地点とC地点」……というように、「ウサギとカメは離れた2地点にいる」としか述べられていないからだろう。
この2地点は距離という尺度で測れて、追いかける方が速ければその距離はだんだん縮まっている、というのが反論の根拠になる。そのうち手が届く距離になっちゃうからね。
ちなみに、身体の大きさがある現実でこれをやるとどうしても途中でぶつかるが、数学的に、数直線上の2つの点同士で鬼ごっこをさせると(最終的に距離差は限りなく0に近づくが)この論理では本当に追いつかない。
ゼノンのゴール設定がアレ
もちろん、普通に鬼ごっこを眺めていれば、どこかのタイミングで追いついてやがて追い抜いてしまう。こんなことが起きるのは「完全に追いつくまでの時間を無限に区切っている」から。
区切りのゴールが「追いついた後」ではなく「追いついた瞬間」にあり、ゴールの手前までを無限に区切っているから、ゴール、つまり追いついた瞬間にはたどり着かないのだ。
つまり、10秒で追いつく鬼ごっこを1秒ごとチェックすれば10回目に追いつくところを見れるのに、ゼノンの論理だと8秒目に見て、9.6秒目に見て、9.9秒目に見て、9.99秒目に見て、さらに9.999秒目に見て……みたいな区切りを永遠に繰り返すから、追いつきそうなのに追いつき切らない瞬間を無限回見ることになる。
11秒目までを区切ることにすれば、追い抜く瞬間は来るのだ。
ゼノンはこのような議論によって、事物を物体の連続的な変化で説明しようとする潮流に抗おうとしたようだ。あれ、数学っぽい話がいつの間にか哲学の話に……。










.jpg)