コジマです。
YouTubeチャンネルのこの企画、内容を説明すると、早稲田大学の小論文の入試問題↓をやってみるというもの。
伸びているこの動画、伸びているだけあって面白かったのだが、私は何でも確率の計算したがるマンなので確率の計算をしたくなってしまった。
私が気になったのは伊沢さんの「キュー以外の手があいこならキューを出した人が勝ち」という案。普通のじゃんけんのルールをそのまま使えてゲーム性も広がるいい案だと思ったのだが、動画の中では「キュー弱くね？」などと言われている。
じゃんけんが優れているのは、どの手にも強い弱いがなくて公平に勝負ができる点である。もしキューが弱い、あるいは強いとしたらゲームには採用しづらいが、そこのところ実際はどうなのだろう。
難しい！
じゃんけんは確率の問題でよく題材になる。普通のじゃんけんの勝敗確率を計算するのも慣れていないと結構難しいが、それにキューを加えたらどうなるのだろう。
腐っても京大生、何とかなるやろ～と軽い気持ちで解き始めたら全然分からなくて困ったが、どうにか求められた。
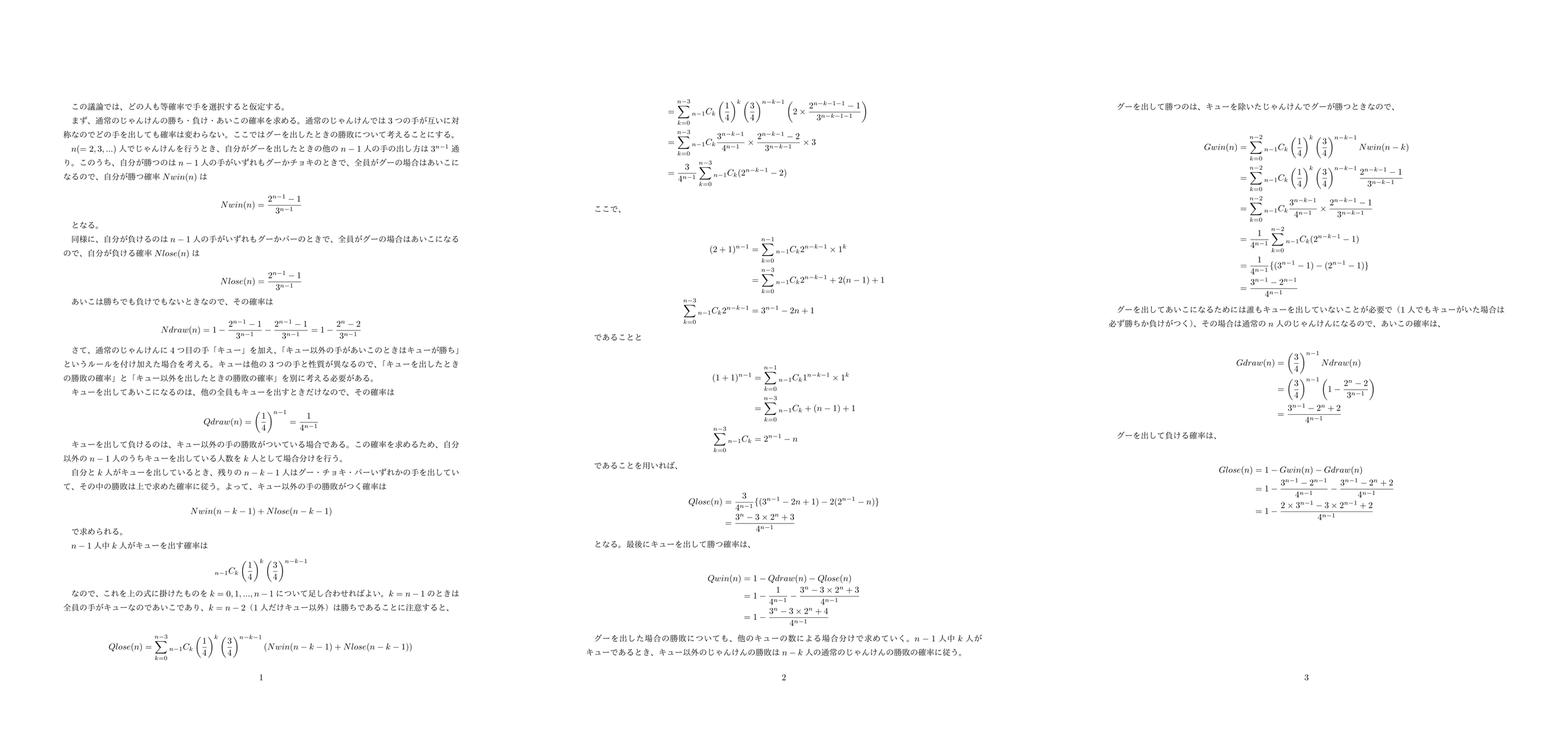頑張って書いたが誰が読むんだ不公平極まりない
式だけ見ても全然ピンと来ないので、具体的に数値で比べてみよう。
まずは普通のじゃんけんの勝率だが、勝ち（青）と負け（黃）が同じ値で、引き分け（赤）の割合が人数が増えるに従って増加するのが分かる。
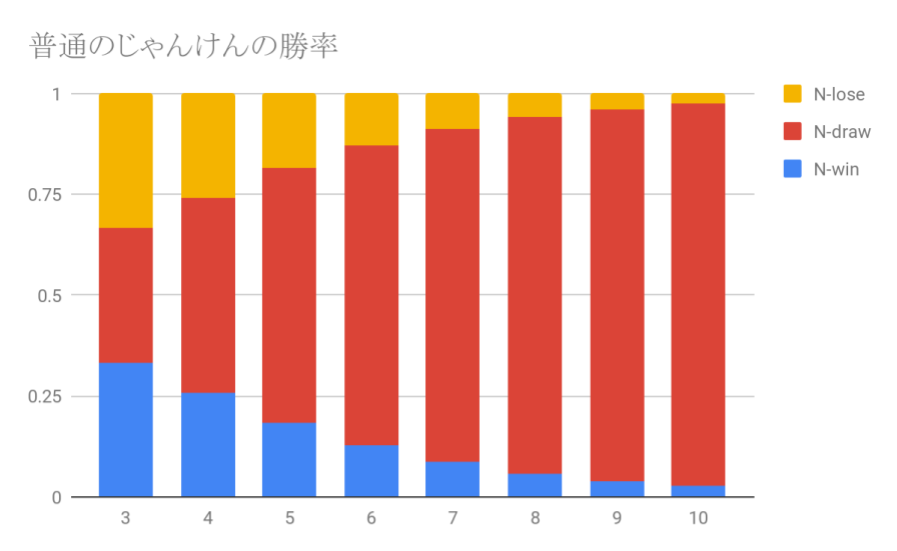
次に、キュー付きじゃんけんのキュー、グー/チョキ/パーそれぞれの勝率を示す。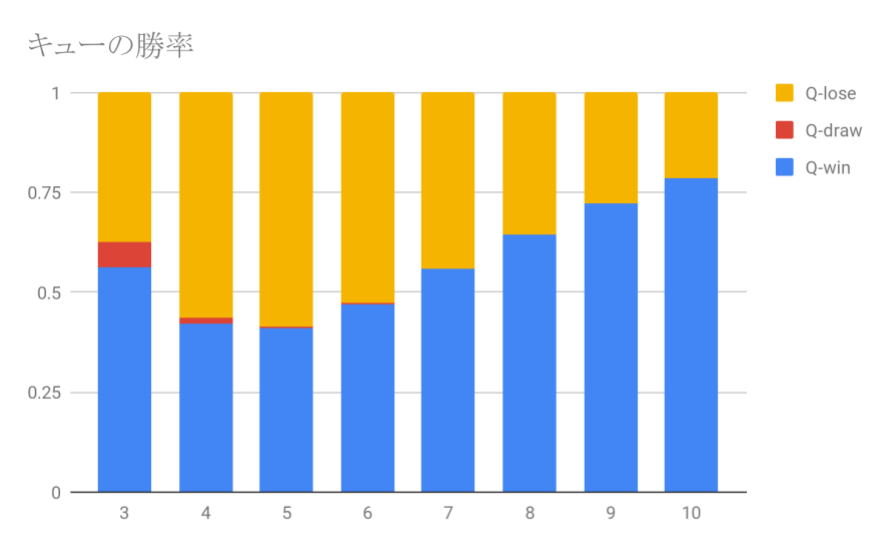
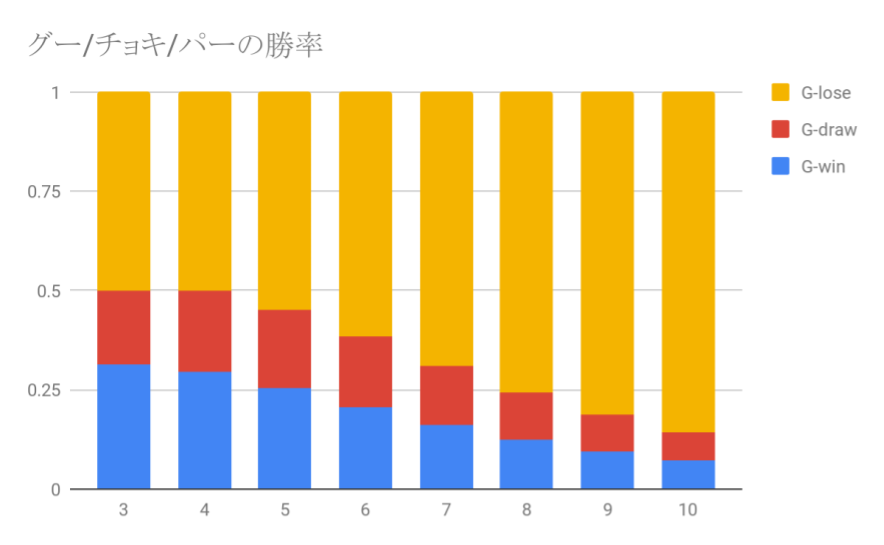
これを見ると一目瞭然だが、伊沢式ではキュー以外の手が絶望的に勝てない。人数に関わらずキューの勝率の方が高く、特に7人以上のじゃんけんではキューを出せば50％以上の確率で勝ててしまうのだ。キュー以外の手の勝率は6人以上で25％未満だから、グーやチョキを出す理由がない。
なお、4～6人でのじゃんけん時はキューの勝率が敗率を下回っているので、その辺が動画内、4人でじゃんけんしていたときの「キュー弱くない？」発言につながっていると思われる。
ただ、ここまで強さに偏りがあると、計算の際に4つの手がそれぞれ同じ確率で選ばれるという仮定を立てたことに無理が出てくる（明らかにキューを出した方が有利なので）。それも含めて駆け引きにはなるかも知れないが。
コジマ案は？
他人の案に文句を言ってばかりでは何も生まれないので、最後に私からもアイデアを出しておきたい。
やはり、動画の須貝さんの案のような対称型になるのが望ましいと思う。忘れていたかもしれないがこれは入試なので、オリジナリティが大事だろう。ルールとは別のルートでアピールだ。
じゃんけんは「グー：石」「チョキ：はさみ」「パー：紙」で強弱を例えるが、「紙が石に強い」は何か納得いかなくないか？と思っていた。
という訳で、ここの間に「キュー：かなづち」を挟むのはどうだろう。かなづちは石を砕けるが、薄い紙には効かない。……どっこいどっこいか。
