解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
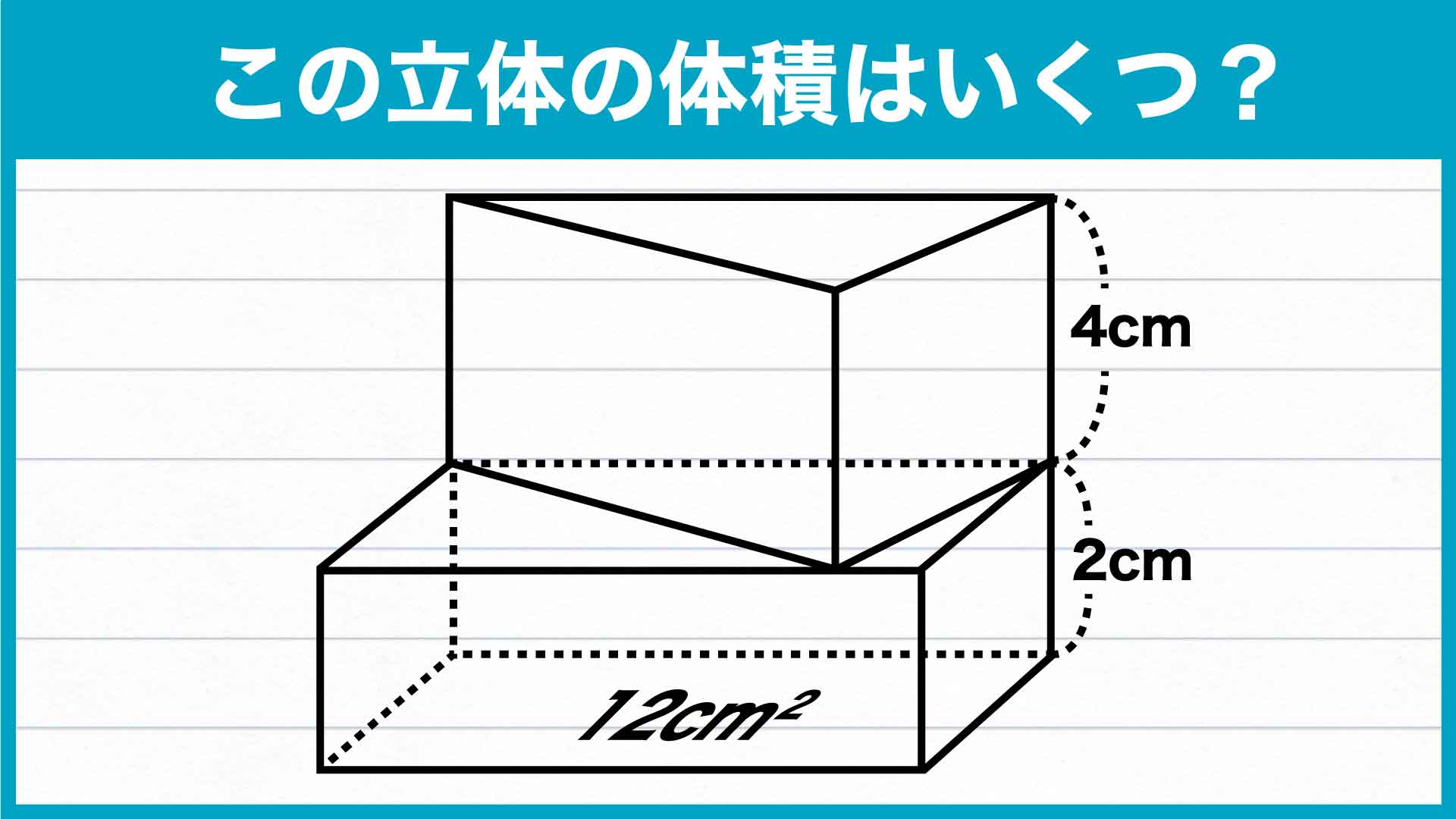
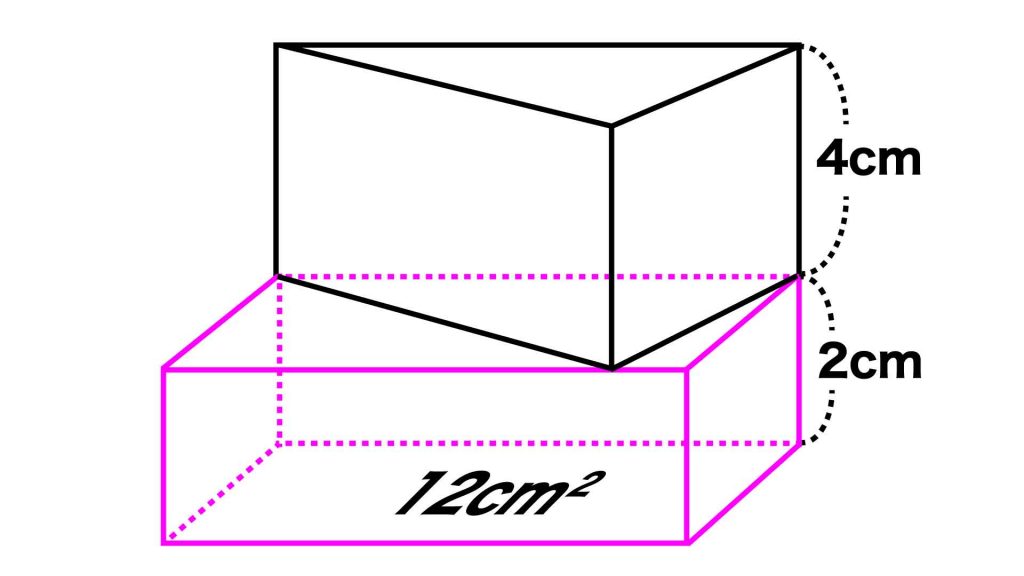
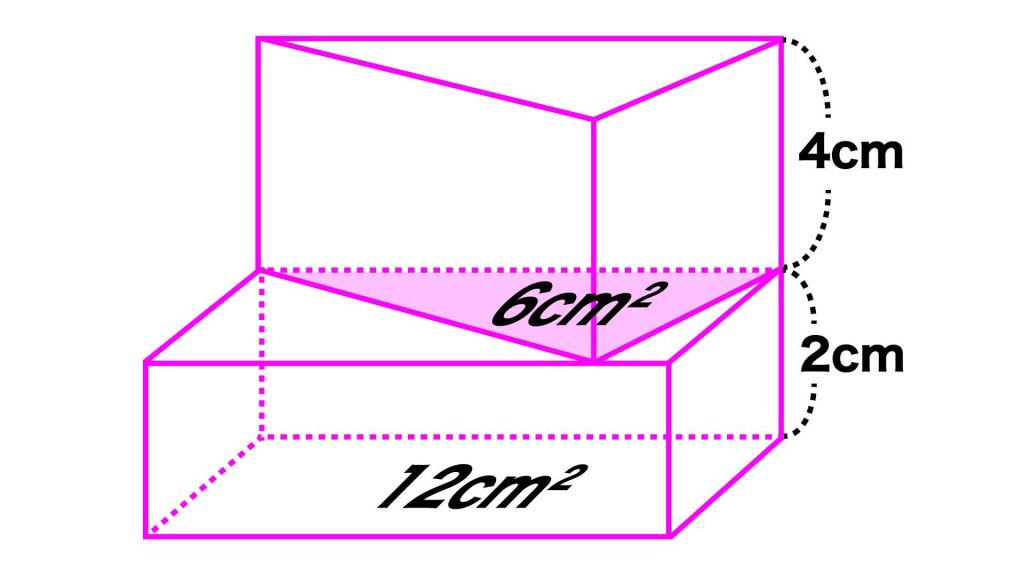
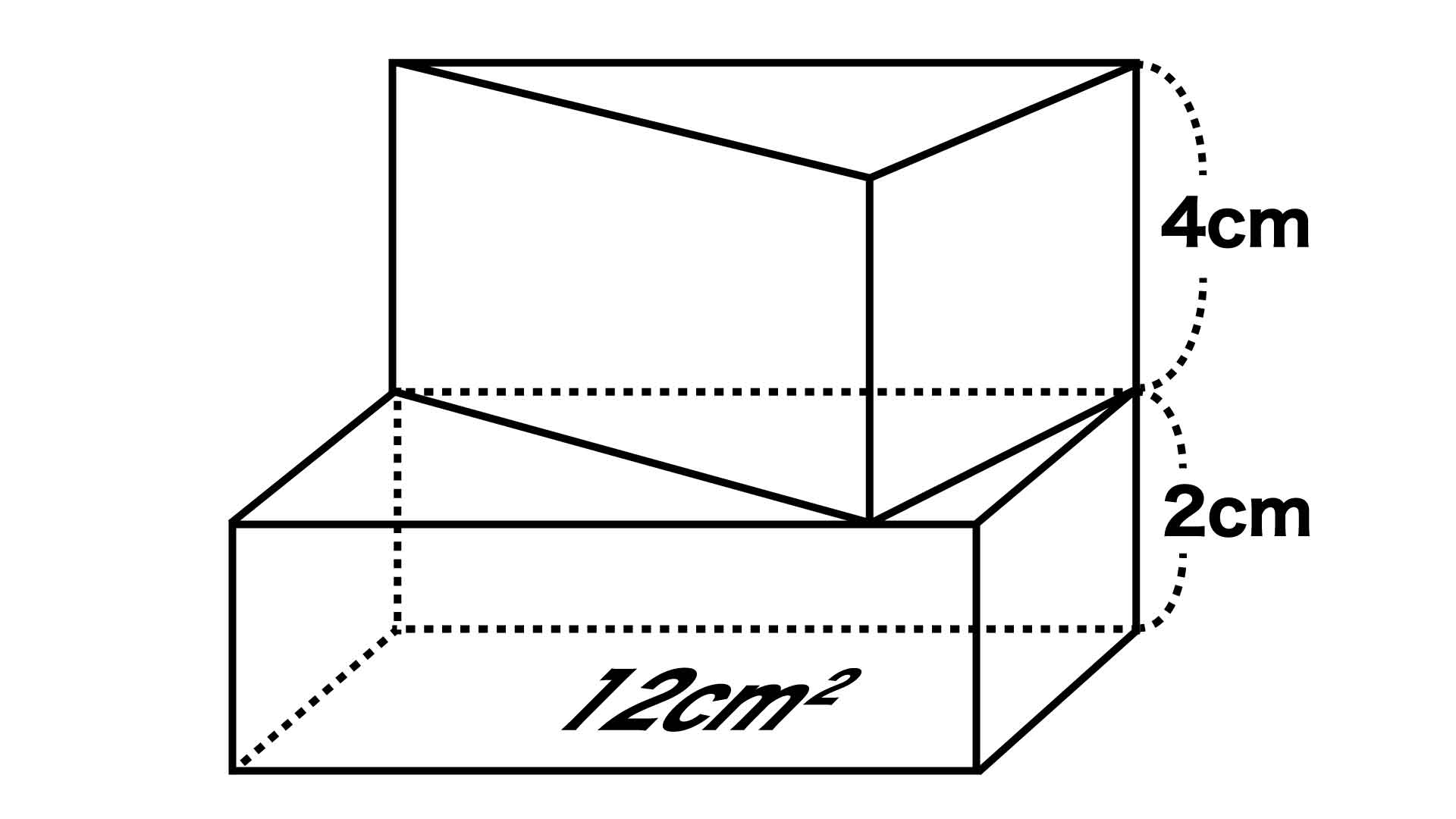▲直方体の底面積がわかっているため、直方体の体積は求めやすいと予測できますね。
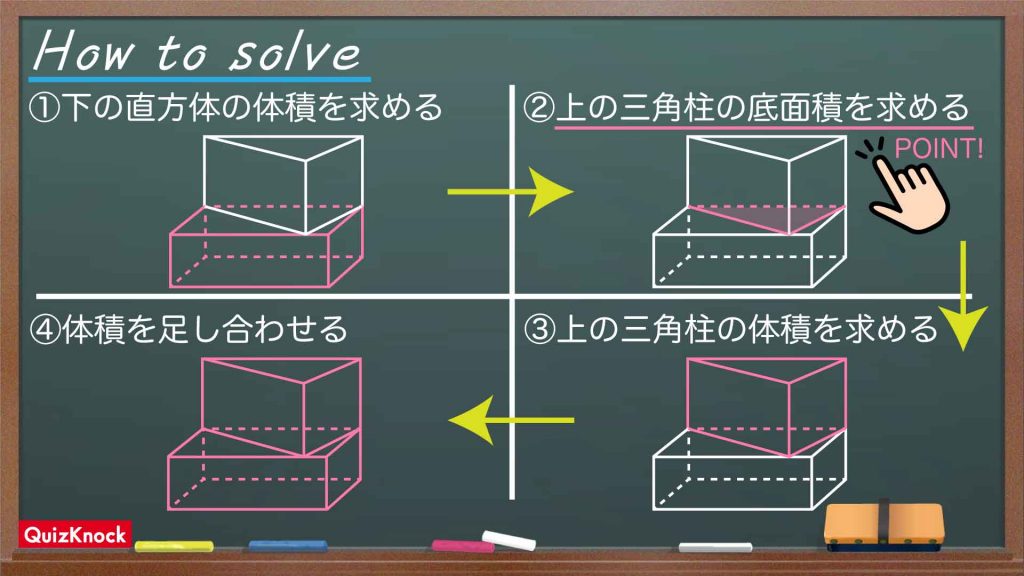
今回は、次の図のように解いていきます。三角柱の体積をどのように求めるかが、この問題の大きなポイントでしょう。
この図の流れに沿って、順に解いていきましょう！
ステップ1：下の直方体の体積を求める
まずは、下の直方体の体積を求めます。
一般的に直方体の体積は、「縦×横×高さ」で求められます。ここで、「縦×横」は直方体の底面積に相当し、その大きさは12cm2であること、また直方体の高さが2cmであることがわかっています。
したがって、直方体の体積は、12×2=24cm3です。
ステップ2：上の三角柱の底面積を求める
このステップが、今回の問題でひらめきが重要になるポイントです。
上の三角柱の体積を求めたいのですが、高さはわかっているものの底面積がわかっていません。
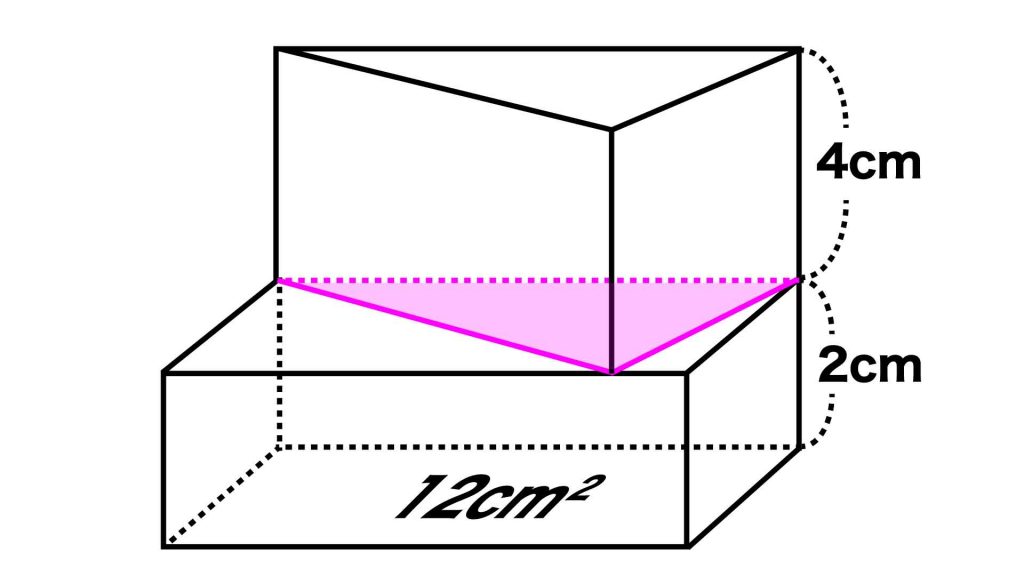
そこで、三角柱の底面積を求めます。
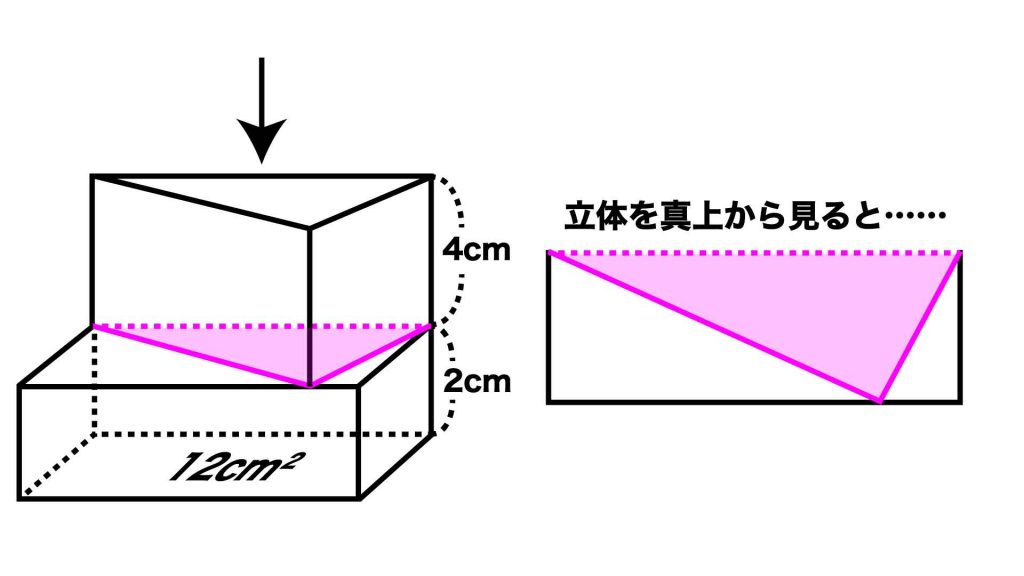
この立体を上から見ると、下の図の右のようになります。
この赤い三角形の面積（三角柱の底面積）は、長方形の面積のちょうど半分です。
なぜなら、三角形の面積は「底辺×高さ÷2」ですが、この「底辺×高さ」の大きさは長方形の「縦×横」、つまり長方形の面積と等しいためです。
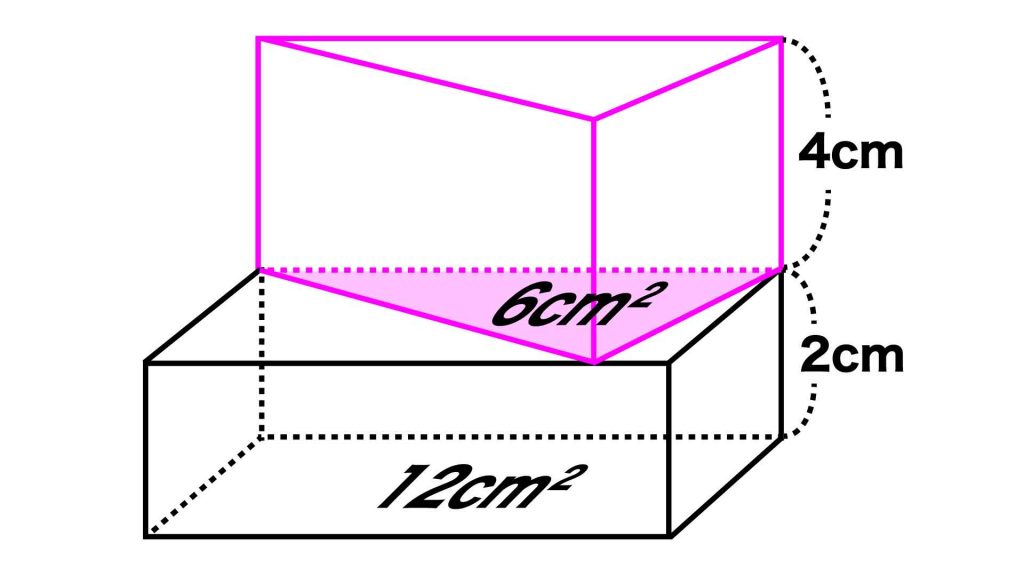
長方形の面積は12cm2であることがわかっているため、赤い三角形の面積（三角柱の底面積）は、12÷2=6cm2です。
ステップ3：上の三角柱の体積を求める
三角柱の底面積がわかったので、体積を求めましょう。
三角柱の体積は、「底面積×高さ」で求められます。
底面積は6cm2、高さは4cmなので、三角柱の体積は、6×4=24cm3です。
ステップ4：体積を足し合わせる
直方体も三角柱も体積を求められたので、これらを足し合わせれば、立体の体積が求められます。
直方体の体積も三角柱の体積も24cm3なので、立体の体積は24+24=48cm3となります。
答え：48cm3
三角柱の底面積をどのように求めるかがカギとなる問題でした。
それでは。
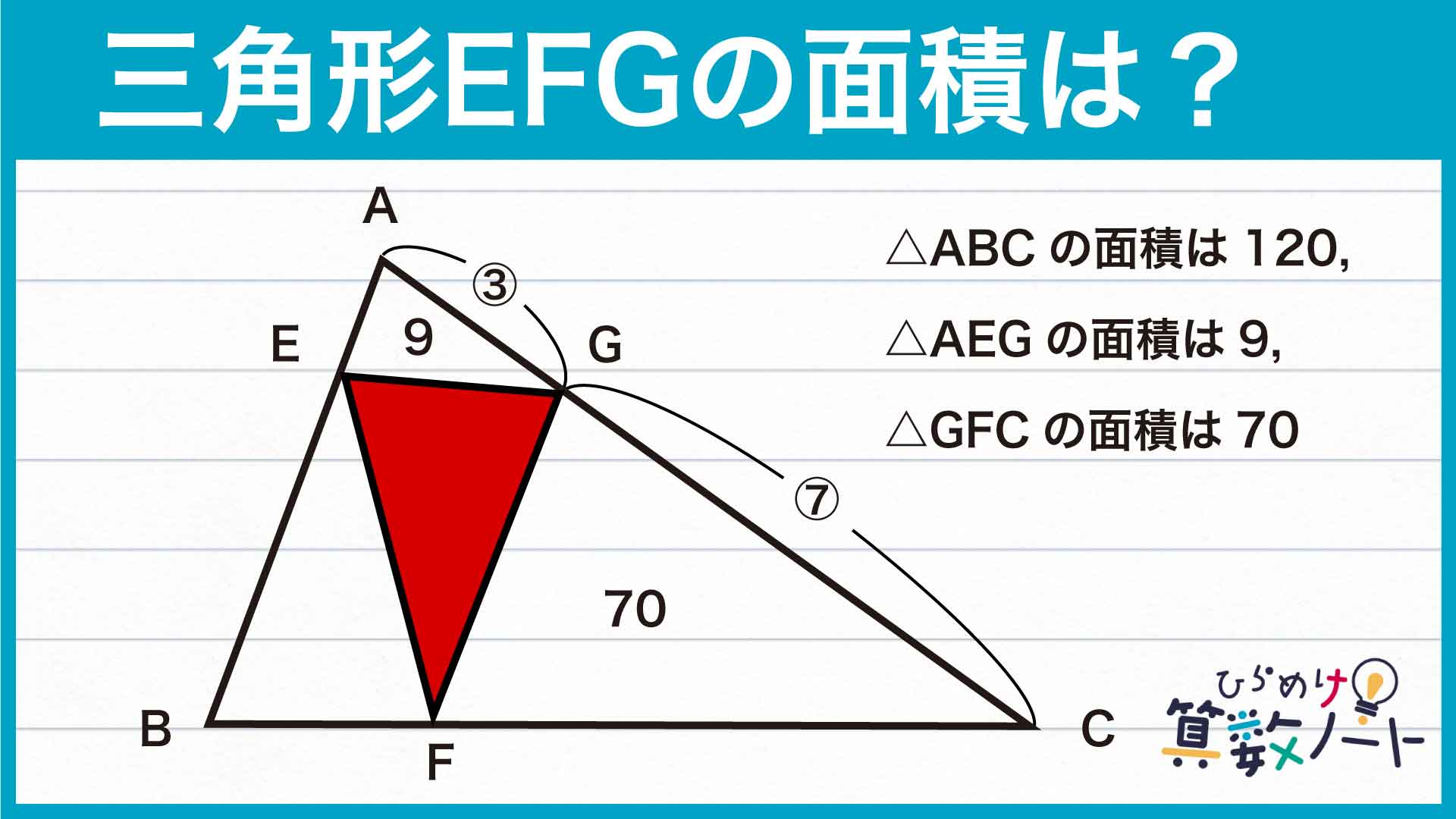
【あわせて読みたい】
