解説
それでは解説です。
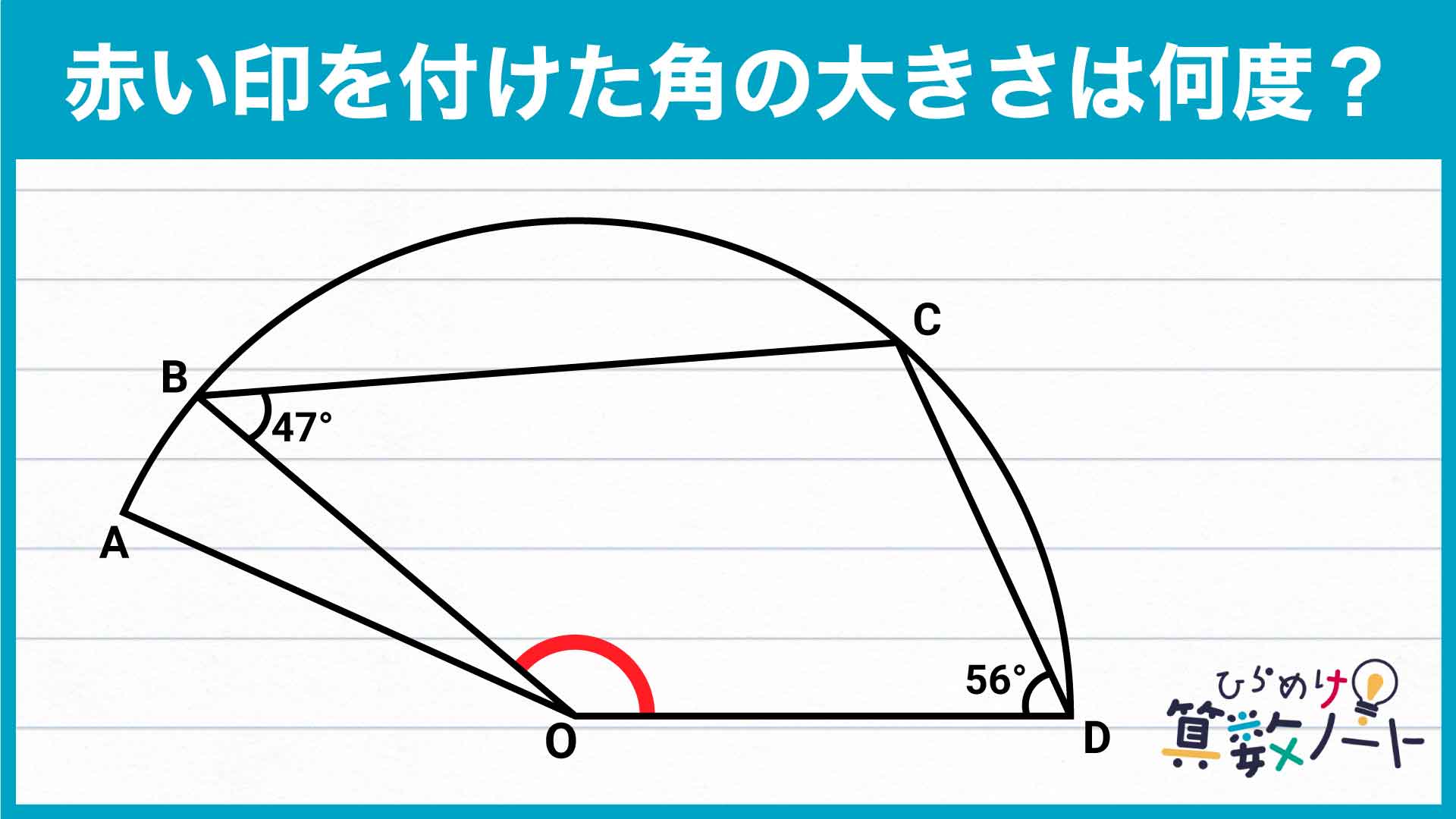
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです。
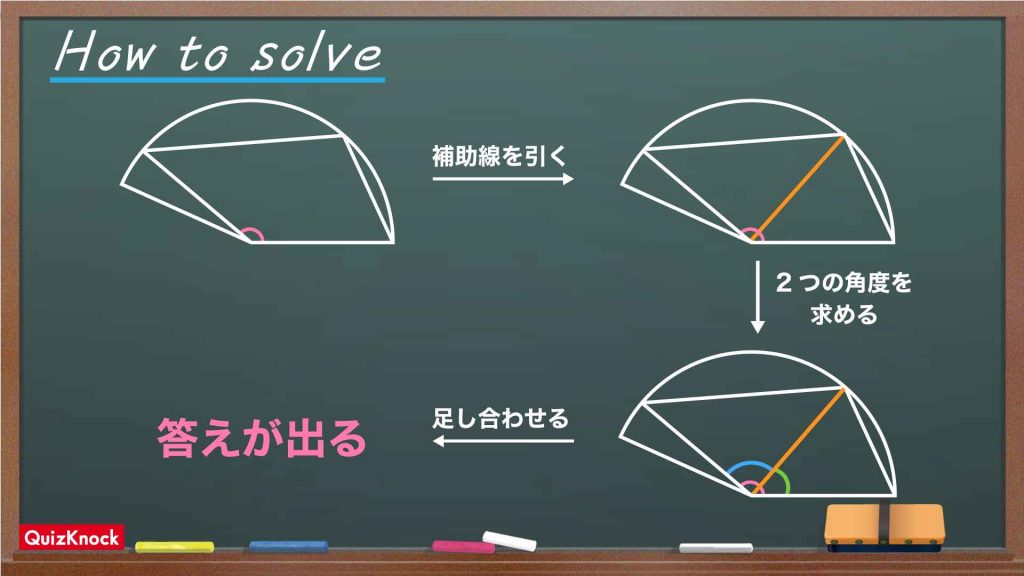
今回の解き方をまとめた図がこちらです。ポイントは、補助線を引いて赤い角を2つの角に分け、それぞれの角度を求めることです。
この流れに沿って、問題を攻略していきましょう!
補助線を引く
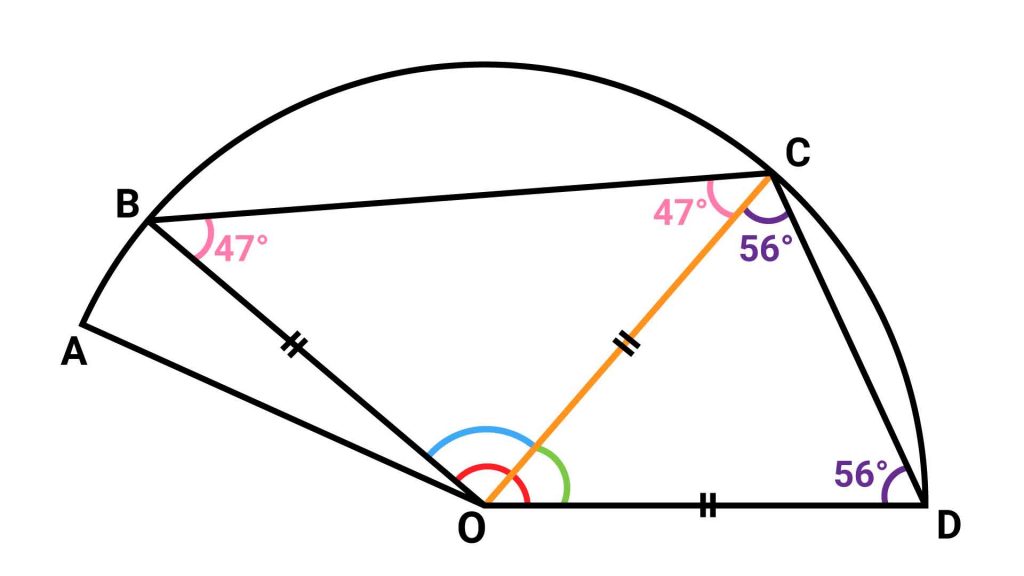
まずは、以下のように点Oと点Cを結ぶ補助線を引きます。
この補助線により、赤い角は角BOCと角CODの2つの角に分けられました。したがって、この2つの角の大きさをそれぞれ求めて足し合わせることで、求めたい角の大きさがわかります。
三角形BOCと三角形CODに注目する
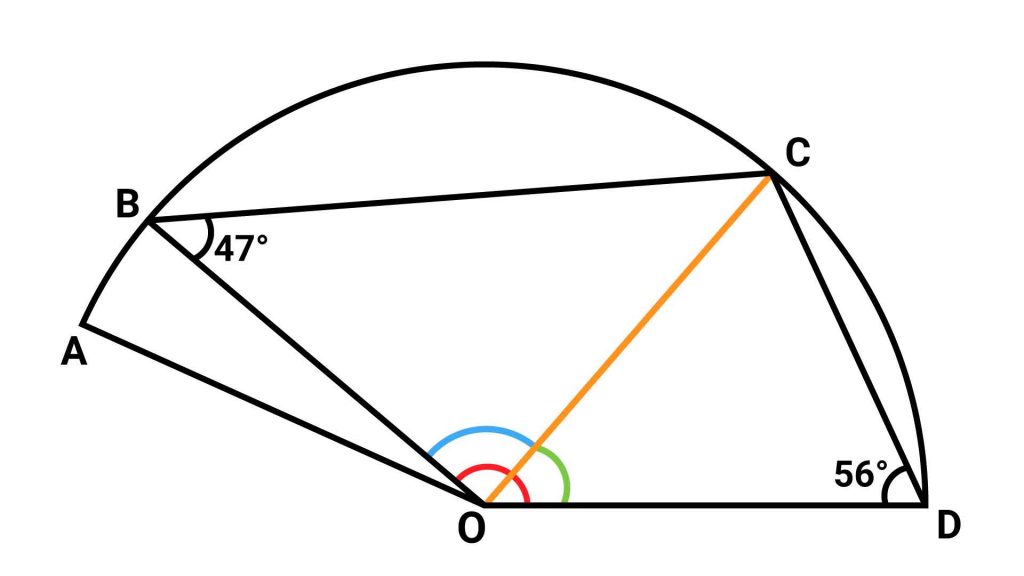
ここで、補助線を引いてできた2つの三角形、三角形BOCと三角形CODに注目します。
OB、OC、ODはいずれも点Oを中心とする円の半径なので、長さは等しくなります。
これにより、三角形BOCと三角形CODはそれぞれ、辺OB=辺OC、辺OC=辺ODの二等辺三角形であるということがわかります。したがって、角OCB=角OBC、角OCD=角ODCとなります。
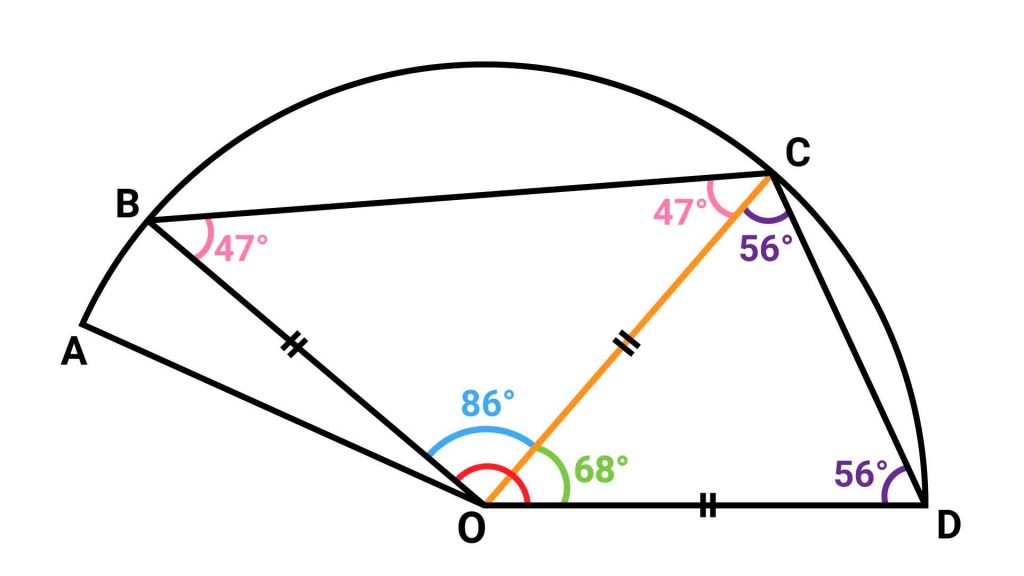
以上より、それぞれの二等辺三角形の2つの角の大きさがわかったので、角BOCと角CODの大きさを求めることができます。それぞれ角BOC=180-(47×2)=86度、角COD=180-(56×2)=68度となります。
求める角=角BOC+角COD
角BOCと角CODは、赤い角を構成する2つの角でした。
したがって、赤い角の大きさは、角BOC+角COD=86+68=154度となります。
答え:154度
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)









.jpg)







