解説
それでは解説です。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです。
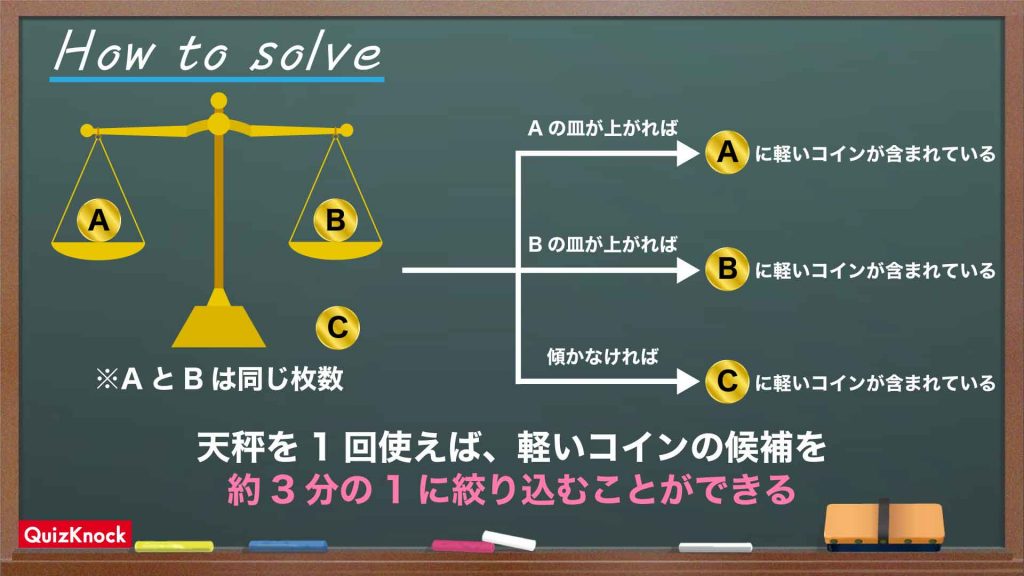
今回の問題の解き方をまとめた図がこちらです。ポイントは天秤を1回使うことで、軽いコインが含まれている可能性があるコインの枚数を、およそ3分の1に絞り込むことができるということです。
この図の流れに沿って、順に解いていきましょう!
天秤を1回使うことでできることは?
天秤を使う回数をできるだけ少なくしたいということから、天秤を1回使うとできることを考えてみましょう。
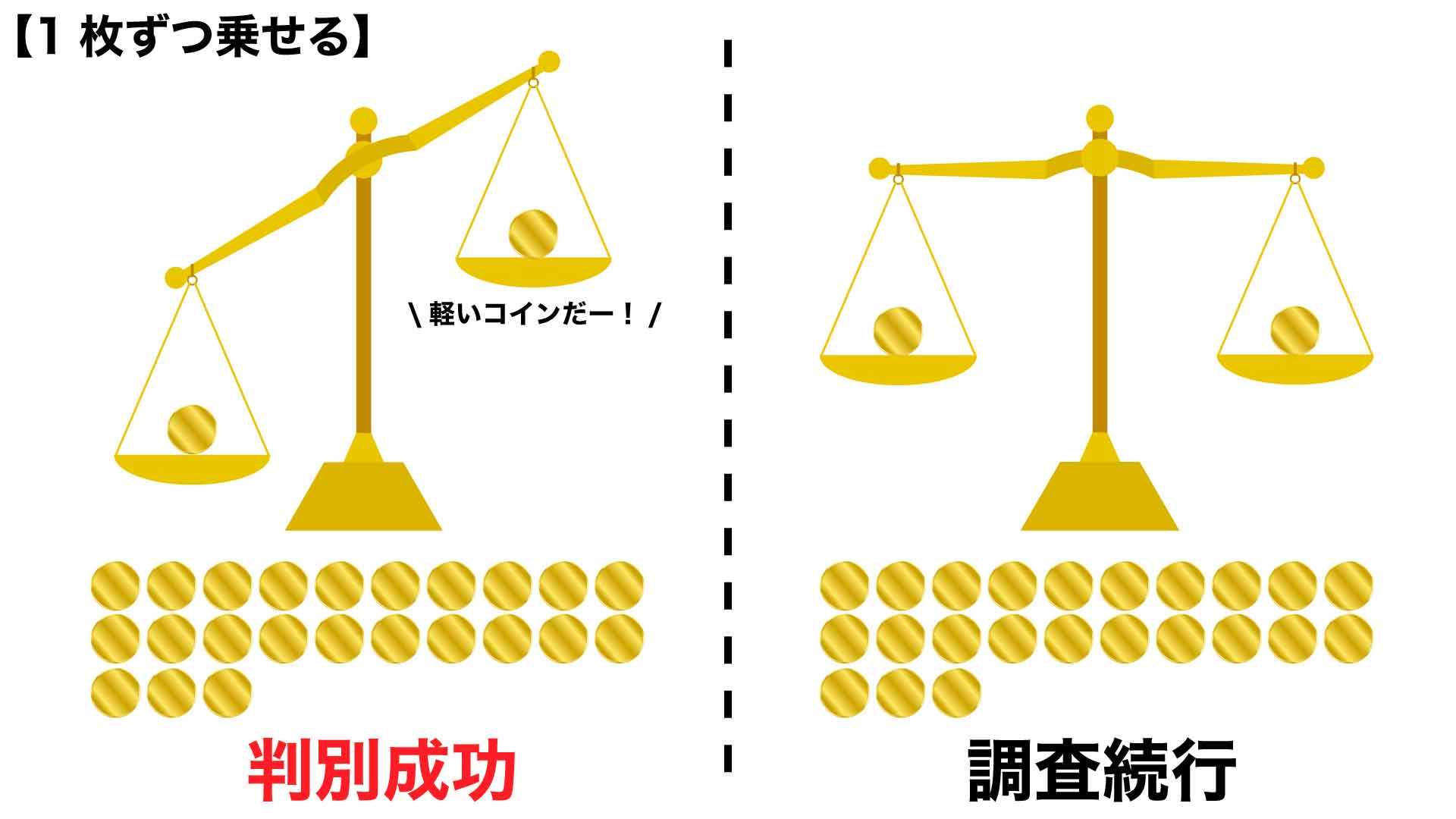
まずは、単純に天秤の両皿にコインを1枚ずつ載せることを考えます。
天秤が傾けば、上がった皿に載っているコインが軽いコインであることがわかり、軽いコインを一発で見抜くことができます。しかし、天秤が傾かなければ、残りの23枚の中に軽いコインが含まれていることがわかりますが、軽いコインの候補をあまり絞れていません。
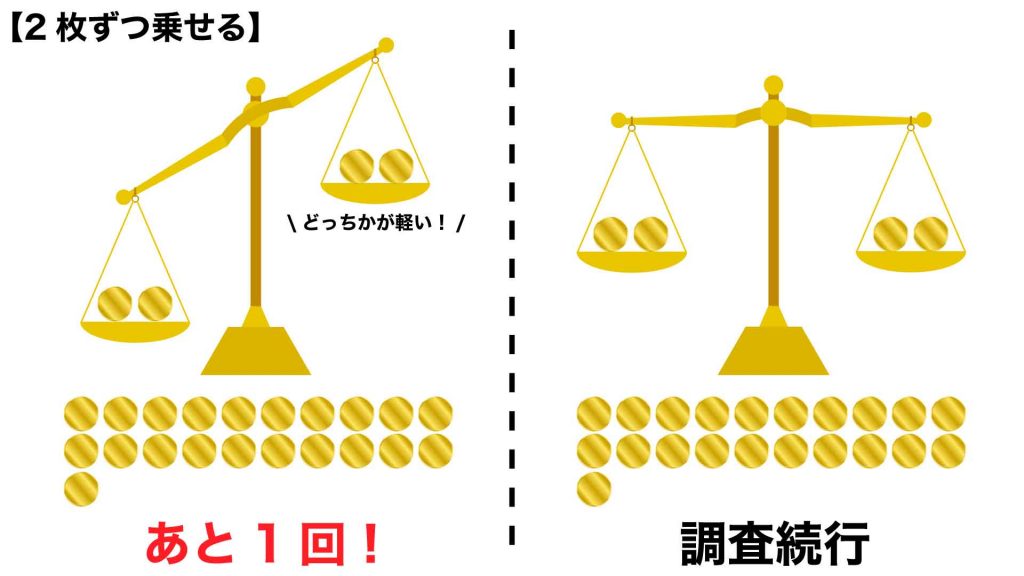
次に、天秤の両皿に2枚ずつコインを載せると、天秤が傾けば軽いコインの候補を2枚に絞ることができます。しかし、天秤が傾かなければ、残りの21枚の中に軽いコインが含まれていることしかわかりません。
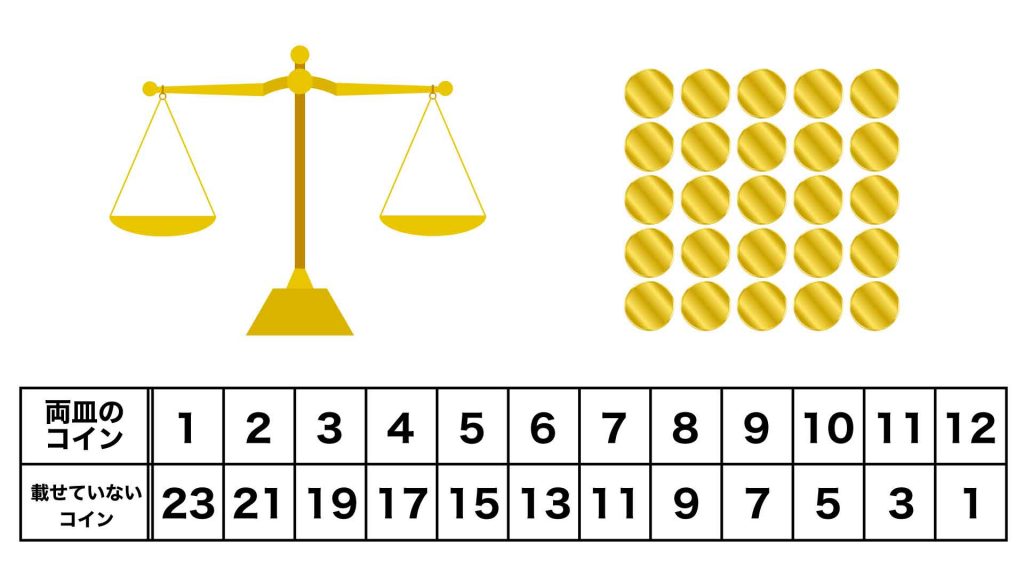
同様にして、天秤の両皿に載せるコインの枚数を1枚ずつ増やしていくと、天秤に載せていないコインの枚数は以下のようになります。
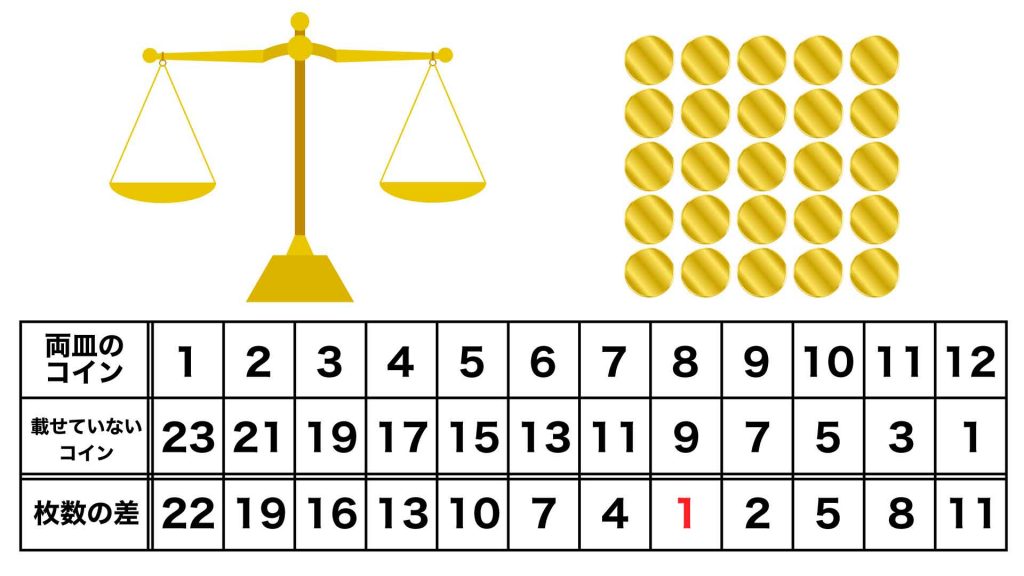
ここで、1回の操作で軽いコインの候補をできるだけ絞りたいため、天秤のそれぞれの皿に載せるコインの枚数と、天秤に載せないコインの枚数の差を考えます。というのは、この差が小さくなるほど、軽いコインの候補をより絞ることができるためです。
軽いコインの候補を最も絞ることができるのは差が最小になるときで、天秤の両皿に8枚ずつコインを載せるときに差が最小になります。したがって、天秤が傾けば軽いコインの候補を8枚に、天秤が傾かなければ軽いコインの候補を残りの9枚に絞ることができます。
できるだけ少ない回数だけ天秤を使用して確実に軽いコインを見分けるには、天秤の傾きの結果にかかわらず軽いコインの候補ができるだけ少なくなることが求められます。そのため、天秤のそれぞれの皿に載せるコインの枚数は、元の枚数(今回の場合は25枚)を3で割ったときの商(今回の場合は8枚)となります。
軽いコインの候補をさらに絞り込む
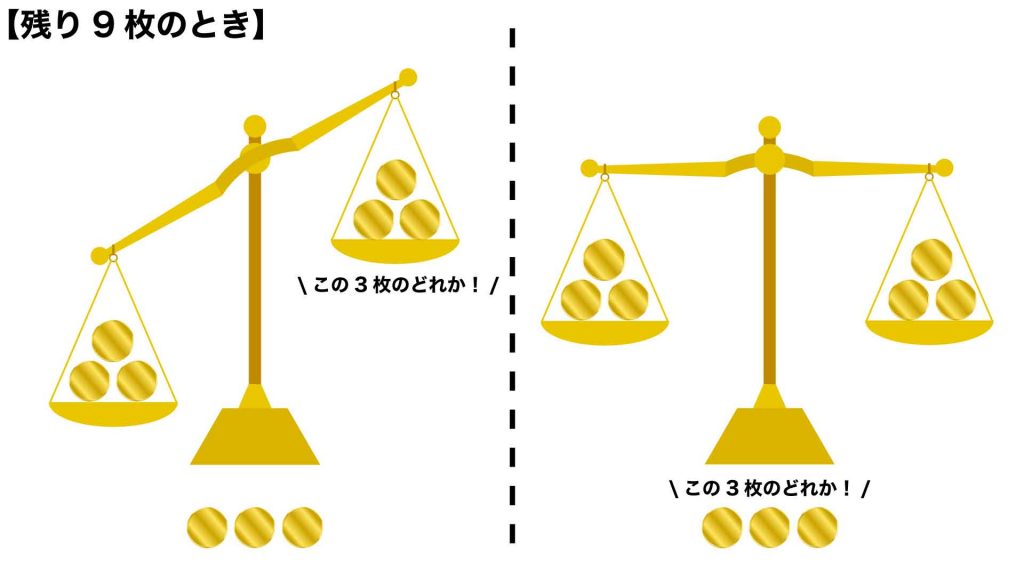
天秤を1回使うことで、8枚か9枚のコインの中に軽いコインが含まれていることがわかりました。
1回目と同様に、天秤のそれぞれの皿に載せるコインの枚数と、天秤に載せないコインの枚数の差を見てみます。
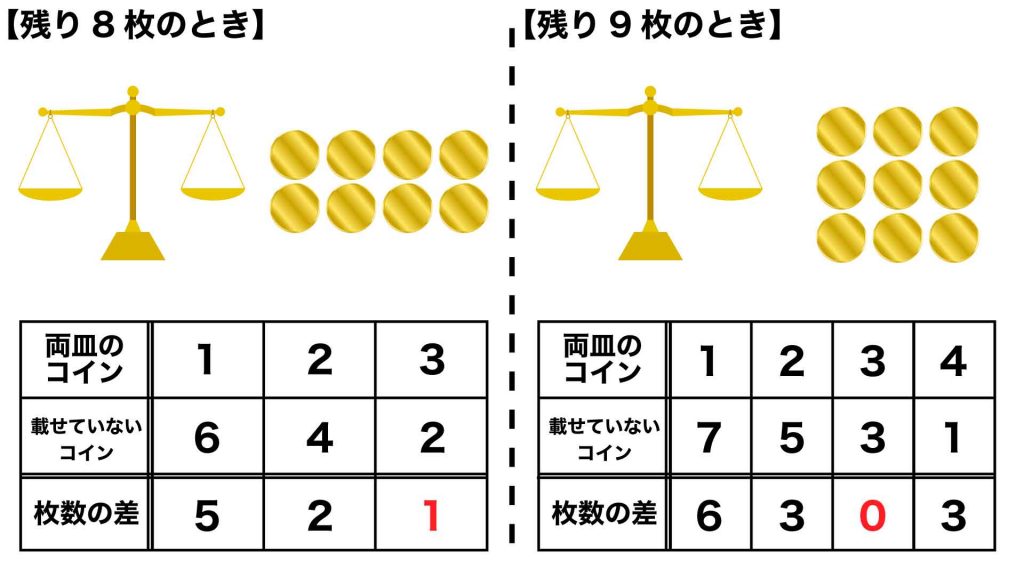
軽いコインの候補が8枚、9枚のいずれの場合でも、天秤の両皿に3枚ずつコインを載せるときに差が最小になります。
天秤のそれぞれの皿に3枚ずつコインを載せると、天秤が傾けば軽いコインの候補を3枚に、天秤が傾かなければ軽いコインの候補を残りの2枚あるいは3枚に絞ることができます。
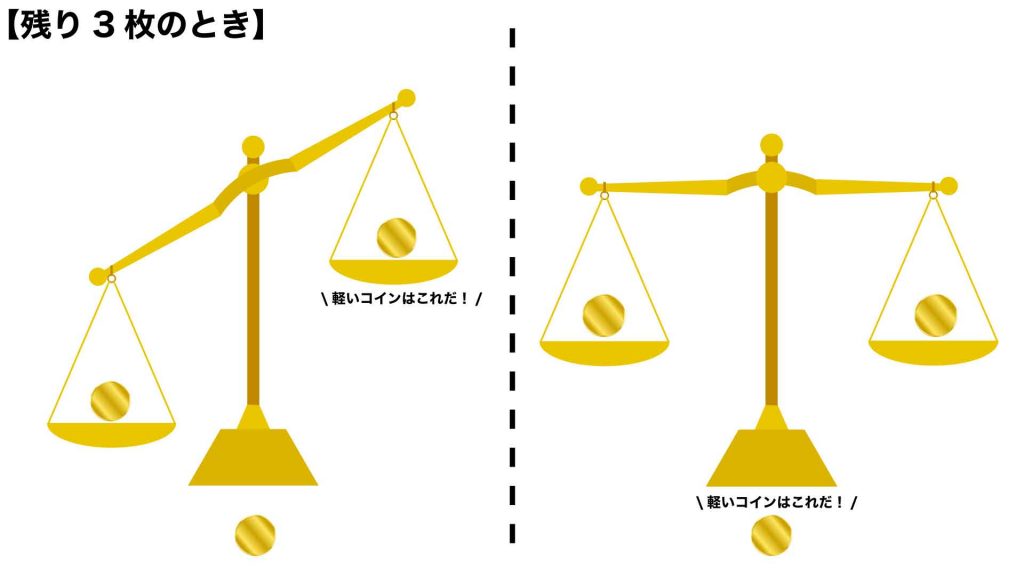
あと一歩!
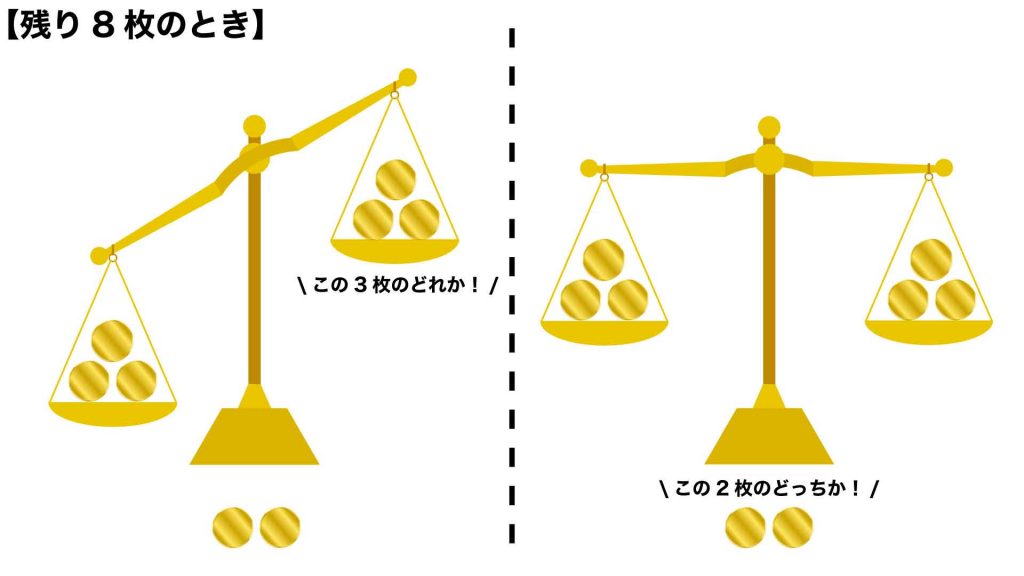
天秤のそれぞれの皿に1枚ずつコインを載せることで、2枚あるいは3枚のコインの中から軽いコイン1枚を見抜くことができます。
天秤が傾けば、上がった皿に載っているコインが、天秤が傾かなかった場合は天秤に載せていないコインが軽いコインであることがわかります。
したがって、天秤を3回使うことで確実に軽いコインを見分けることができます。
答え:3回
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】












.jpg)










.jpg)







