解説
それでは解説です。この問題についてはさまざまな解き方がありますが、ここでは「小学5年生で解ける」解き方を紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです。
今回の問題で重要なポイントは、次の2点です。
- 四角形EFGHがどんな四角形かを調べる
- 図形を動かす(スーパーひらめきポイント!)
この2つのポイントに着目すると、魔法のように面積を求めることができます。
四角形EFGHはどんな四角形?
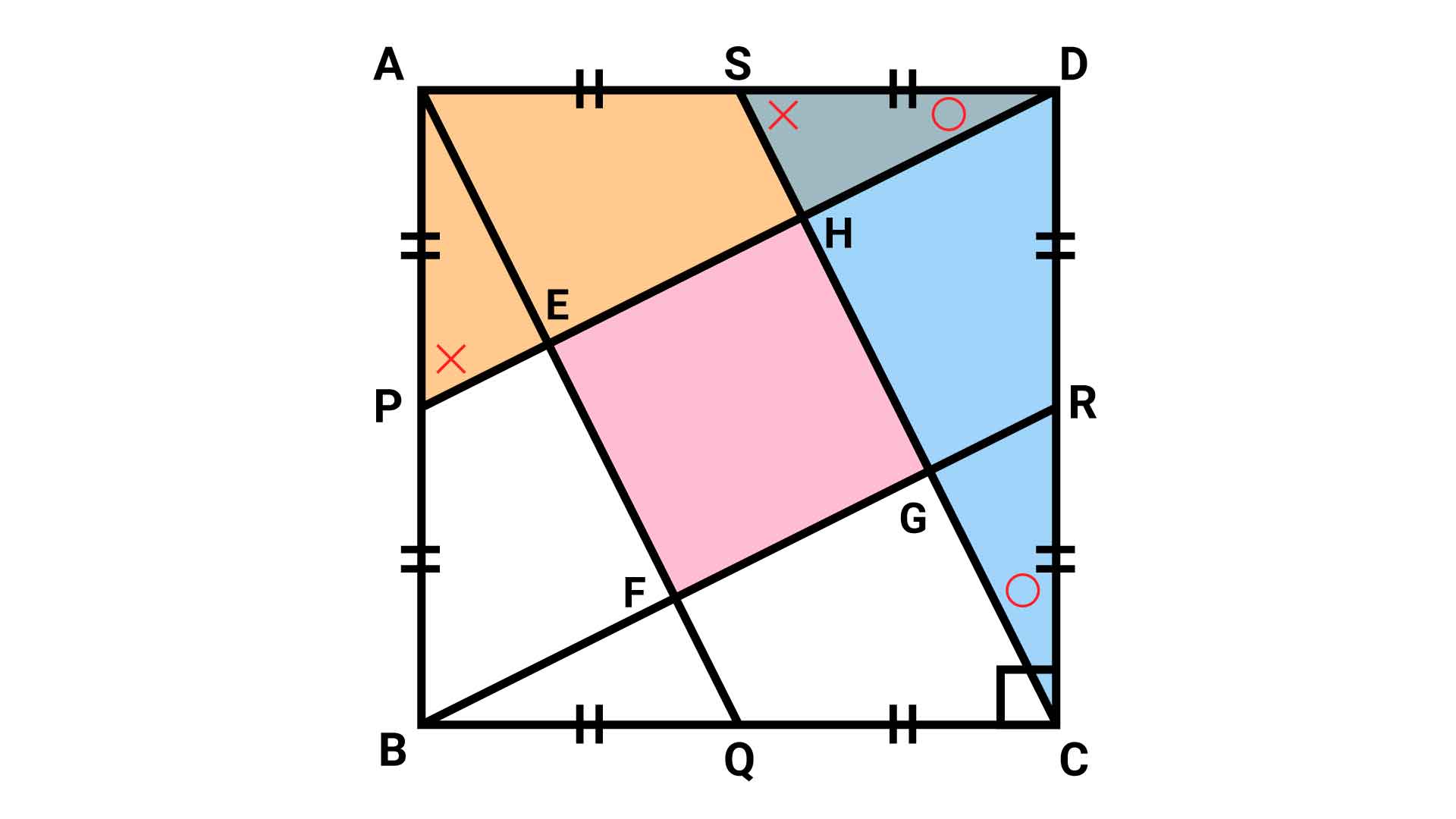
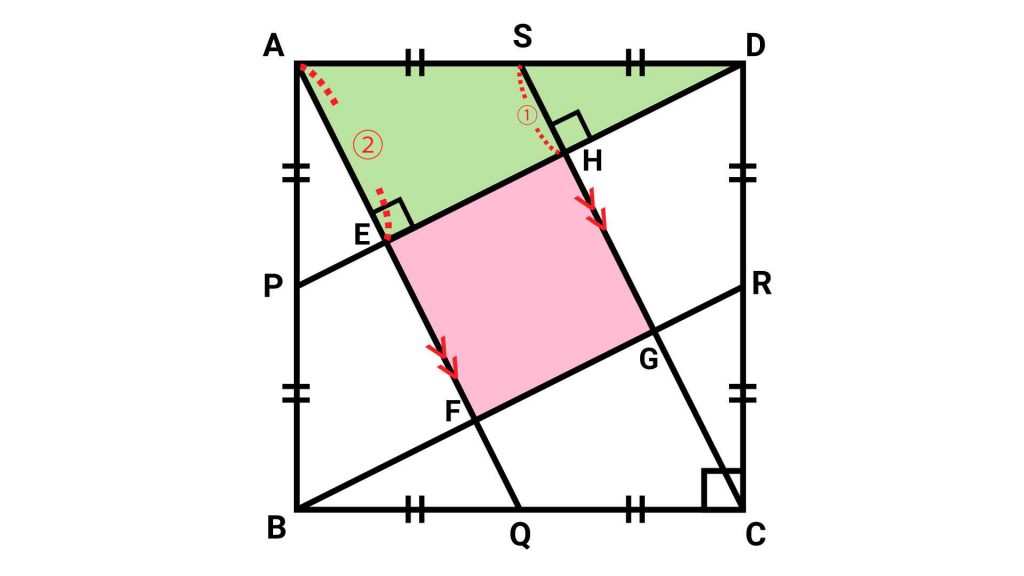
まず、四角形EFGHがどんな四角形かを考えます。着目すべきは、2つの三角形ADPとDCSです。
この2つの三角形は、
- 角PAD=角SDC=90度(四角形ABCDが正方形であるため)
- AD=DC
- AP=DS
が成り立っており、2つの三角形の2辺の長さと、2辺に挟まれた角の大きさが互いに等しくなっています。
したがって、この2つの三角形は合同であるため、対応する角の大きさがそれぞれ等しくなります。
三角形ADPについて、三角形の内角の和が180度であることから、〇+×=90度が成り立ちます。
ここで、三角形SDHに着目すると、角SHDの大きさが90度となるため、四角形EFGHの1つの内角の大きさが90度であることがわかります。
上と同様の考え方を三角形ABQと三角形BCRについても行うことにより、四角形EFGHのすべての内角が90度であることがわかります。
図形を移動させる
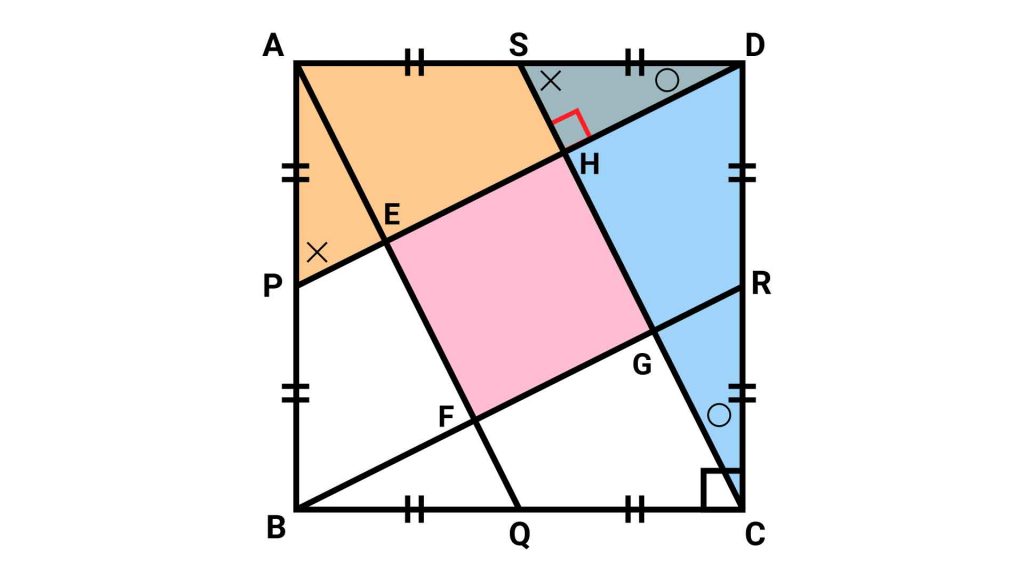
次に、三角形DAEに着目します。
角AEDと角SHDがともに90度であることから、AQとSCは平行です。
また、DSとDAの長さの比が1:2であることから、三角形DAEは、三角形DSHの各辺を2倍に拡大したものであることがわかります。
したがって、SHとAEの長さの比は1:2となります。
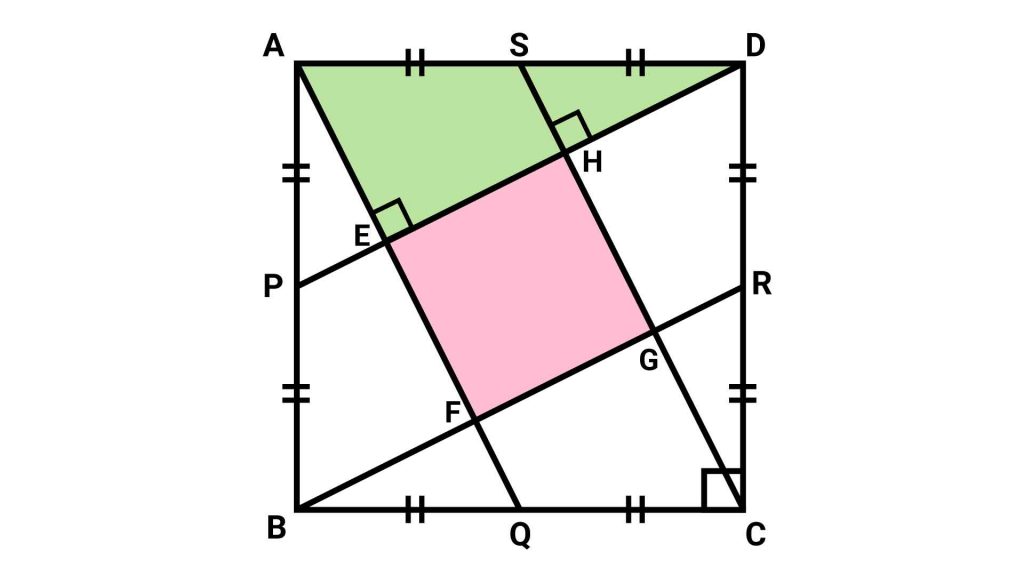
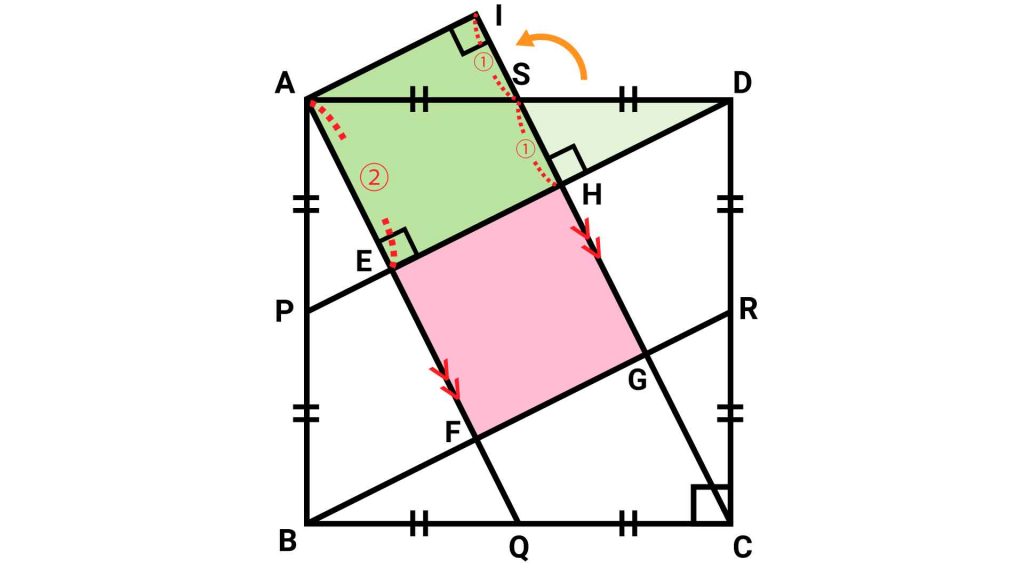
ここで、三角形DSHを、Sを中心にしてDとAが重なるように回転させます。
この操作によってHが移る点をIとすると、四角形AEHIについて、
- すべての内角が90度
- AE=AI(三角形APEとDSHが合同なので、AE=DH=AI)
が成り立つため、四角形AEHIは正方形となります。
残りの三角形も移動させよう!
残りの三角形についても、同様に移動させます。
せっかくなので、問題の図をプリントアウトして、実際に移動させてみました。
まず、三角形を切り離します。
そして、移動させると……?
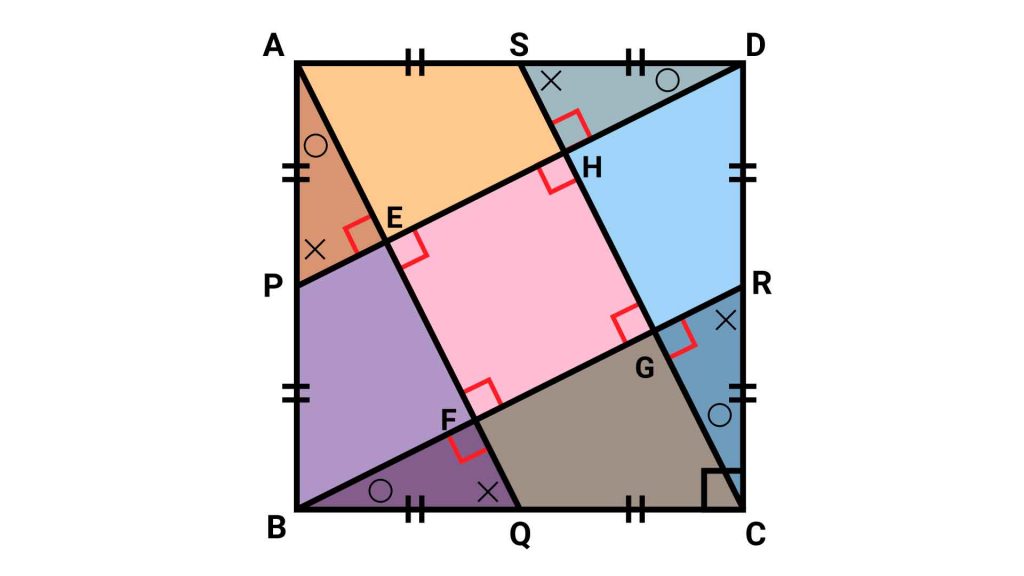
このような図形になりました!
合同な図形から作られた白い4つの正方形は、全く同じ大きさになります。そして赤い四角形は、全ての白い正方形と辺を共有しているため、同じ大きさの正方形になります。
すなわち、三角形を移動させることで、設問の図が、同じ大きさの正方形5つに変身します。
もとの図形の面積は10×10=100cm2なので、赤い正方形の面積は、100÷5=20cm2となります。
答え:20cm2
それでは。
【前回の算数ノートはこちら】
【あわせて読みたい】









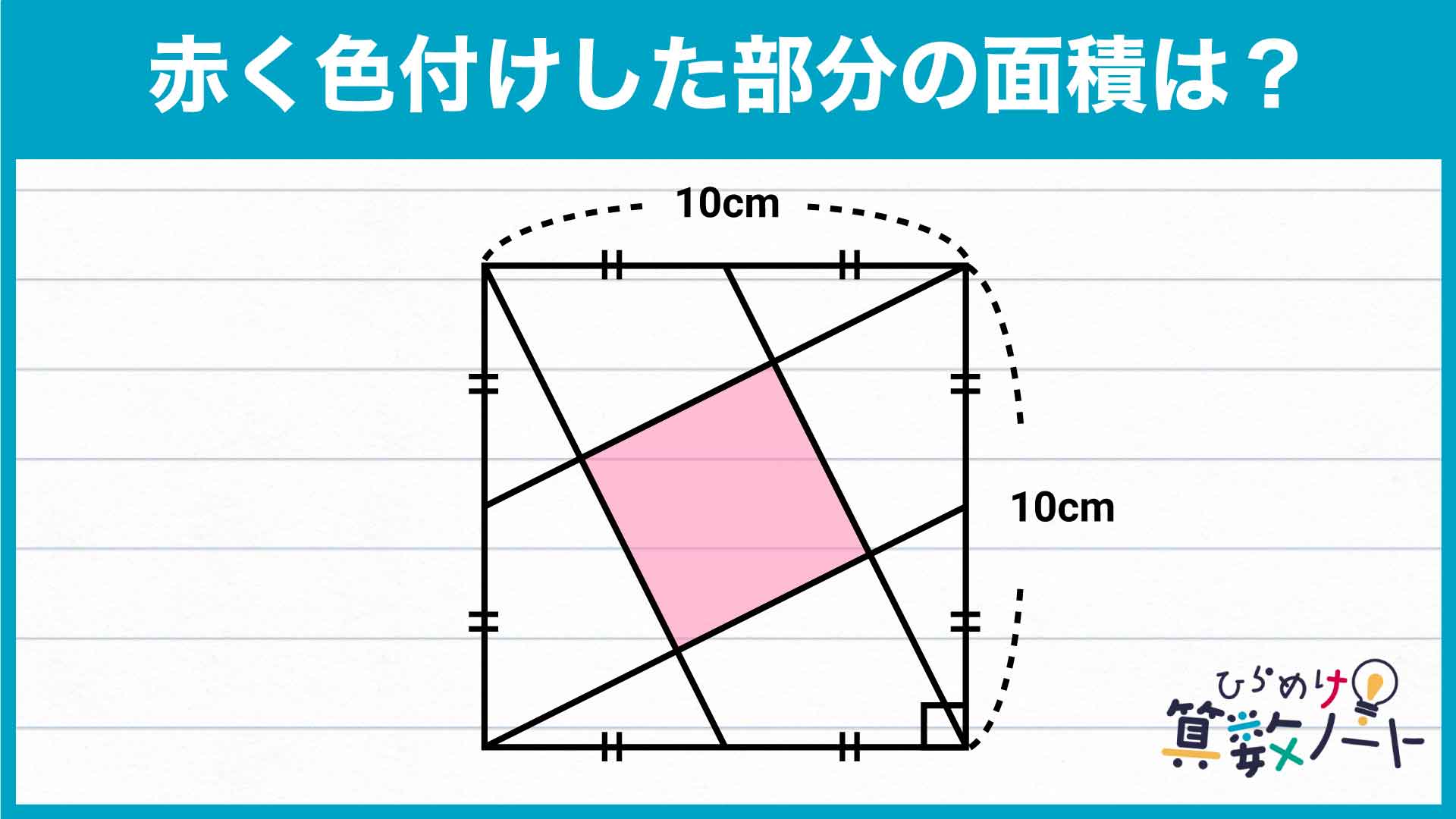

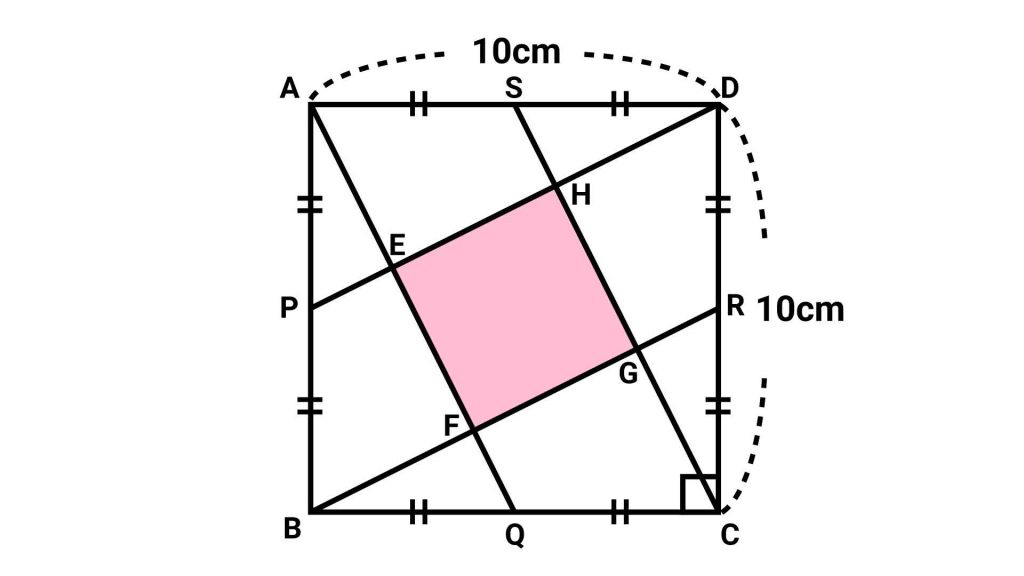
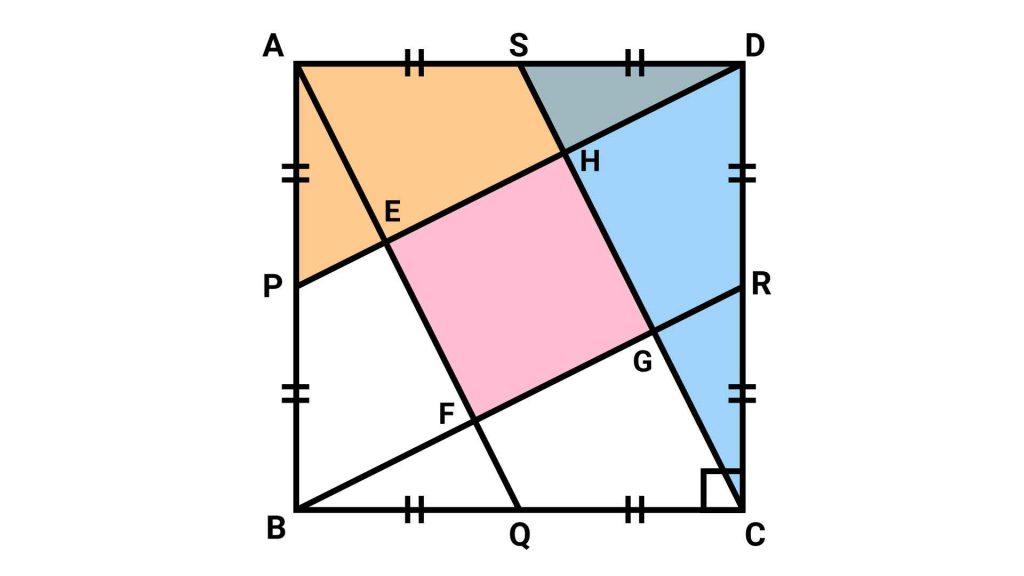



.jpg)









.jpg)