正方形の面積をひらめきで導け！小学5年生レベルの算数クイズに挑戦

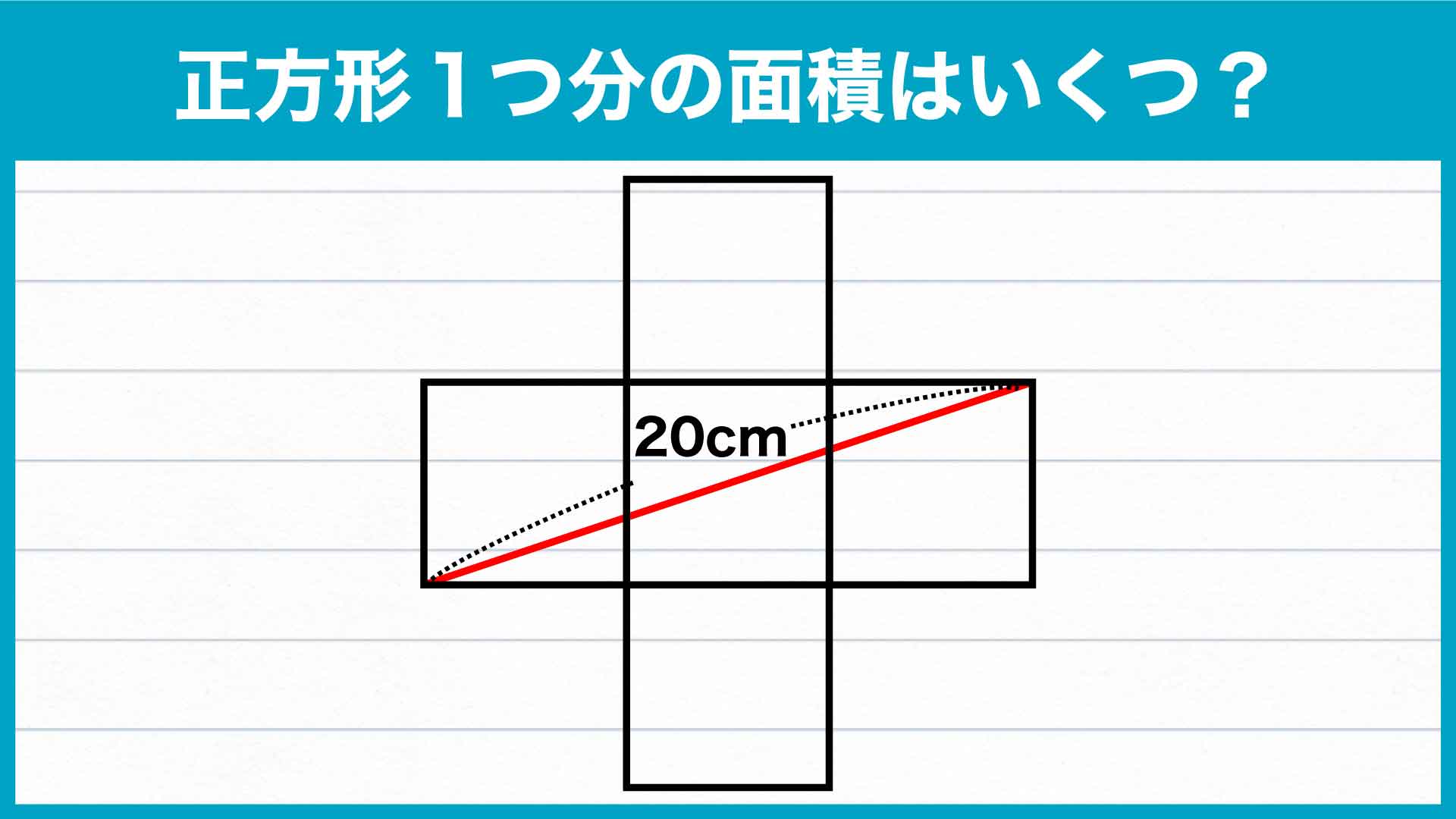
解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

今回の問題で重要なポイントは、「補助線を引いて、赤線を対角線とする正方形をつくる」ことです。

この正方形をつくることで、設問の正方形の面積が簡単に求められるようになります。その方法を解説していきます！

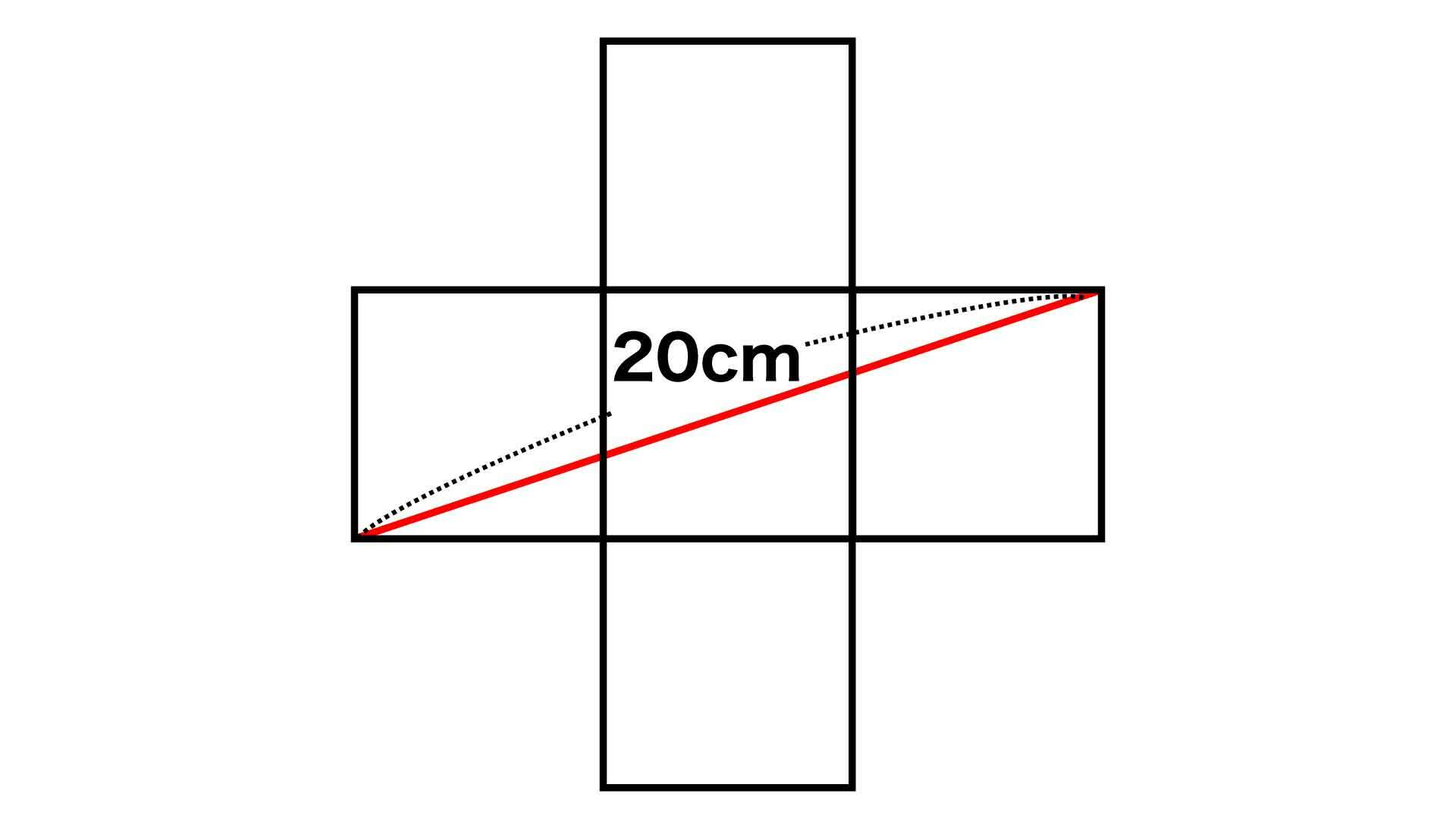
補助線はどこに引く？

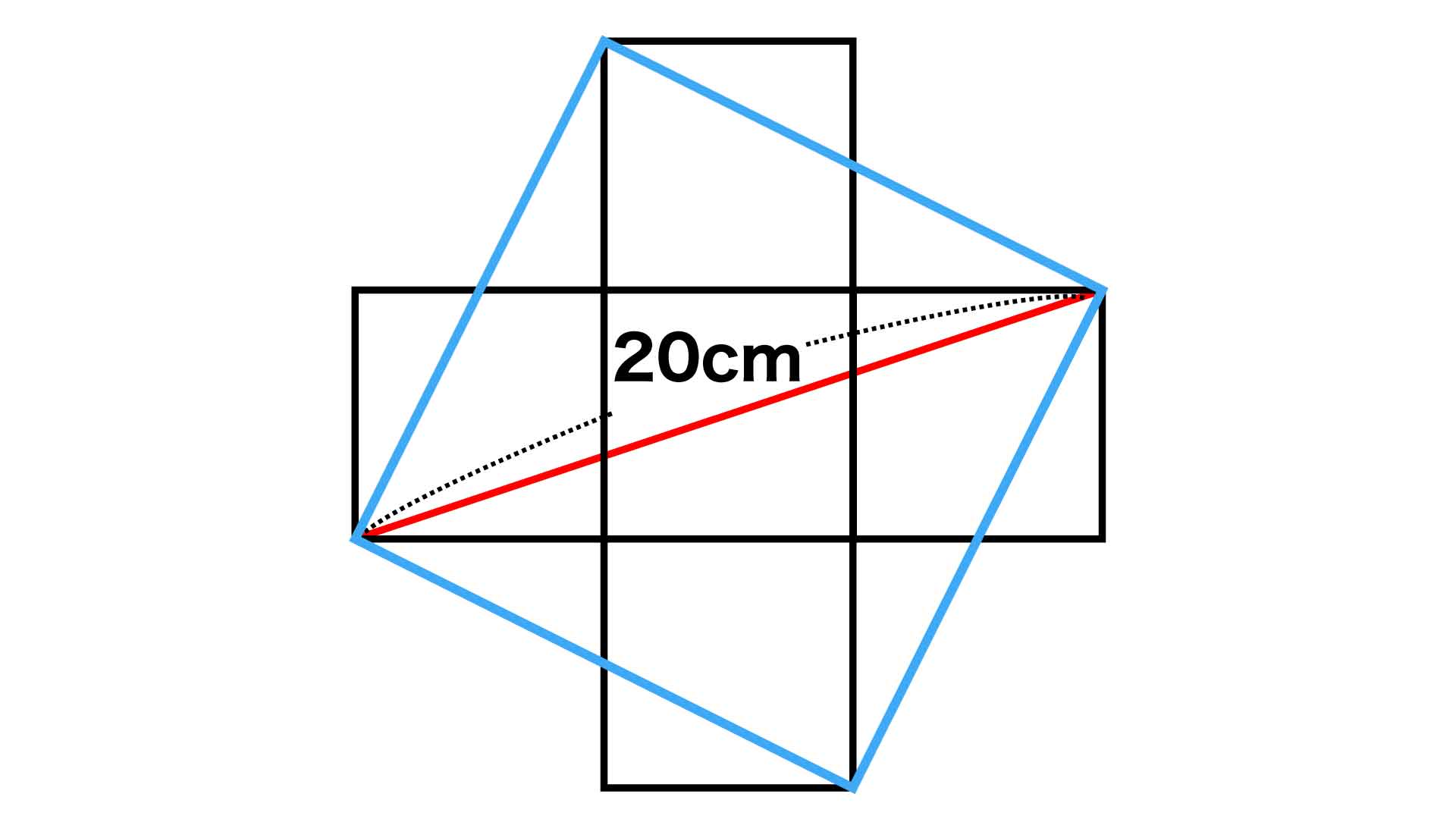
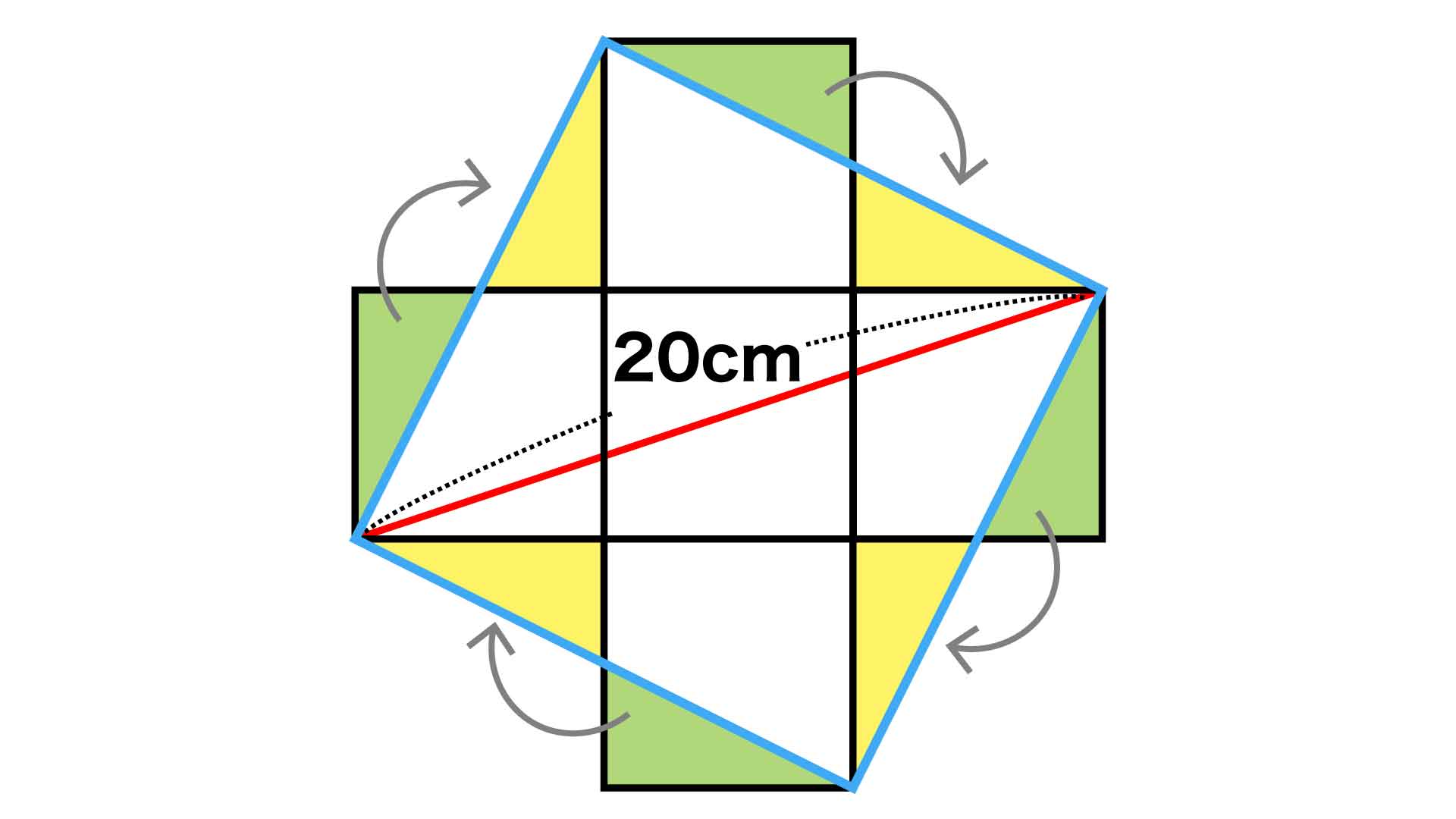
下の図の青線のように補助線を4本引くと、赤線を対角線とする正方形をつくることができます。

はみ出た図形の性質を調べる

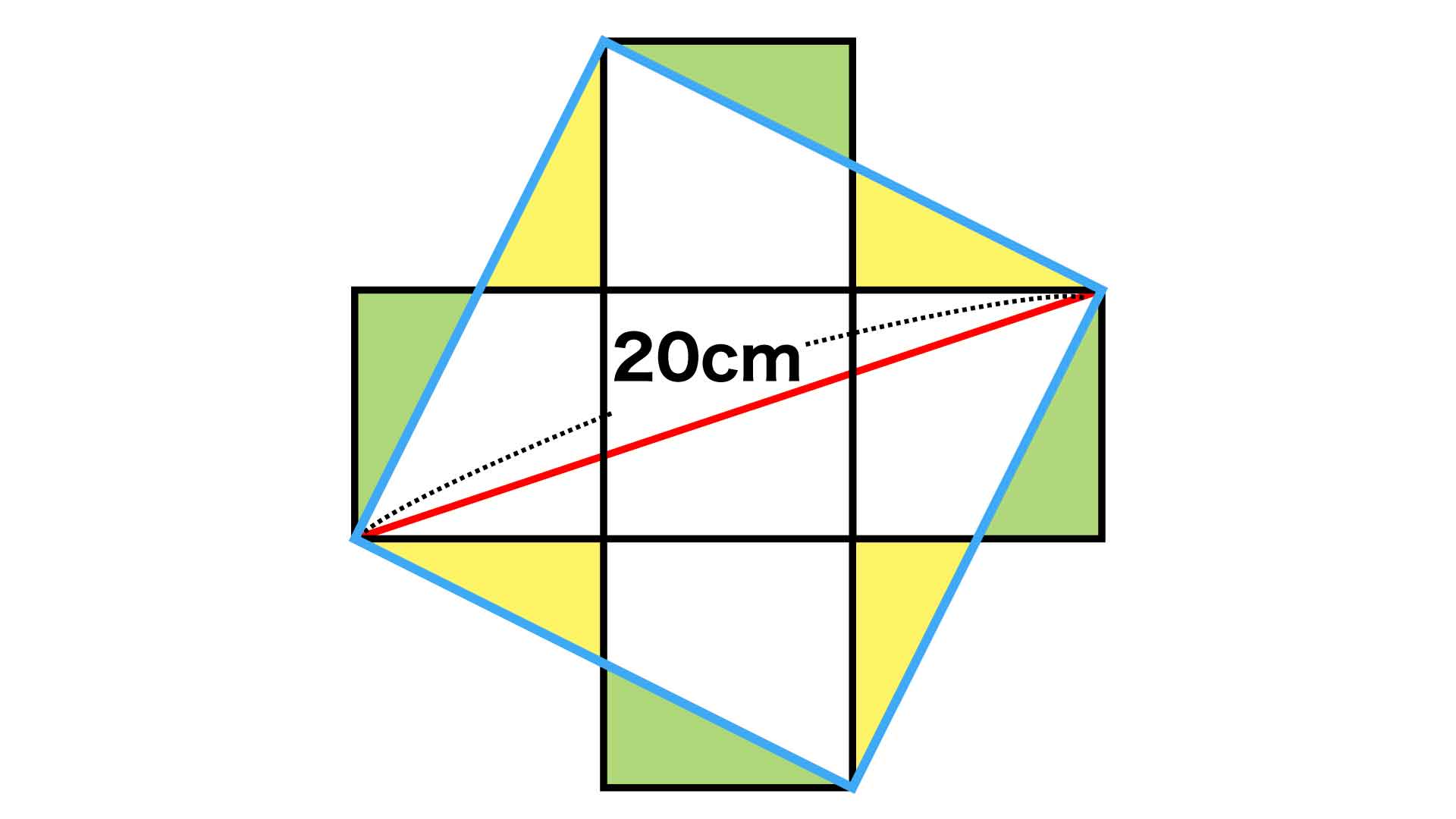
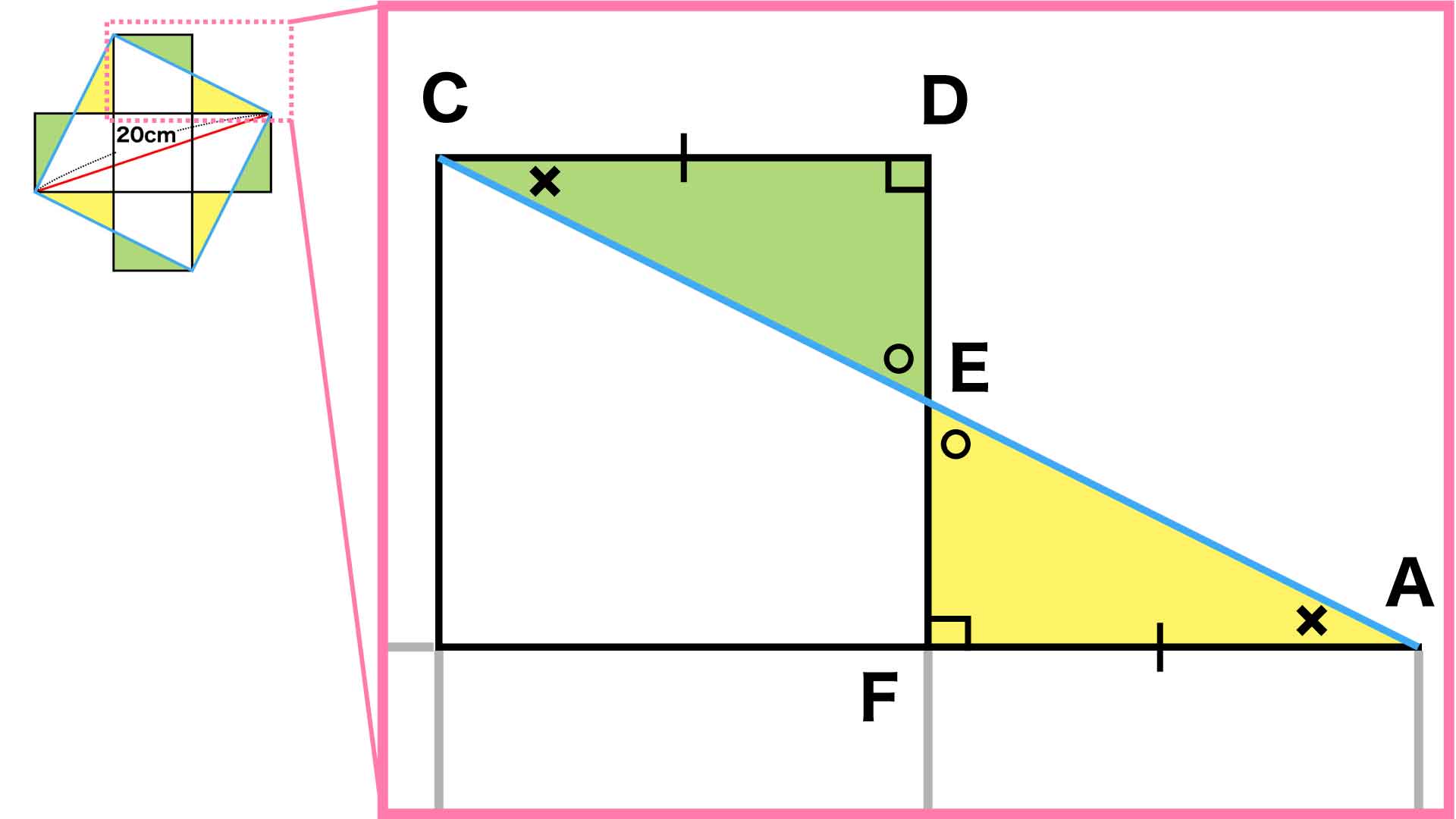
補助線を引くと下の図のように、青線の正方形からはみ出した緑色の三角形と、青線の正方形の内側に黄色の三角形ができています。

まず、同じ大きさの正方形の一辺なので、辺CD=辺AFです。

2つの直線が交わるときに向かい合う角（対頂角）は等しいことから、角CED=角AEFとなります。また、正方形の角なので、角EDC=角EFA=90度です。

2つの角が等しく、三角形の内角の和は一定（180度）のため、残りの角も等しくなり、角ECD=角EAFとなります。

したがって、1つの辺とその両端の角度が等しいので、緑色の三角形と黄色の三角形は合同、つまり面積が等しいことがわかります。

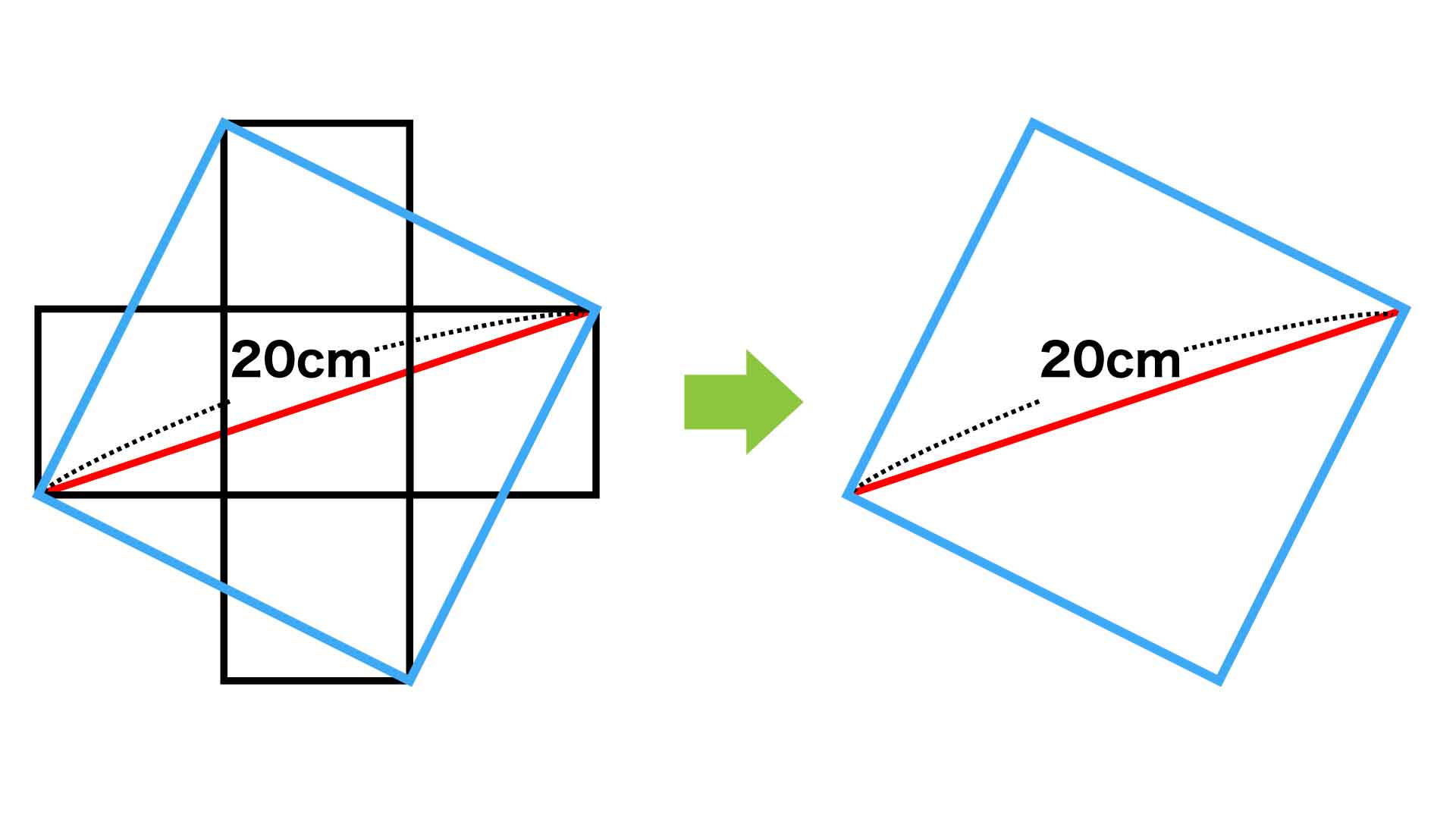
これにより、青線の正方形からはみ出した緑色の三角形は、黄色の三角形にぴったり重なります。つまり、5つの小さな正方形の合計の面積は、青線の正方形の面積と同じであることがわかりました。

青線の正方形の面積を求める

正方形の面積は、ひし形の面積を求める式「（対角線）×（対角線）÷2」で求められるため、青線の正方形の面積は、20×20÷2=200cm²となります。

青線の正方形の面積は、求めたい正方形の面積5つ分と同じ大きさでした。

よって、求めたい正方形1つ分の面積は、200÷5=40cm²となります。

答え：40cm²

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】