解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
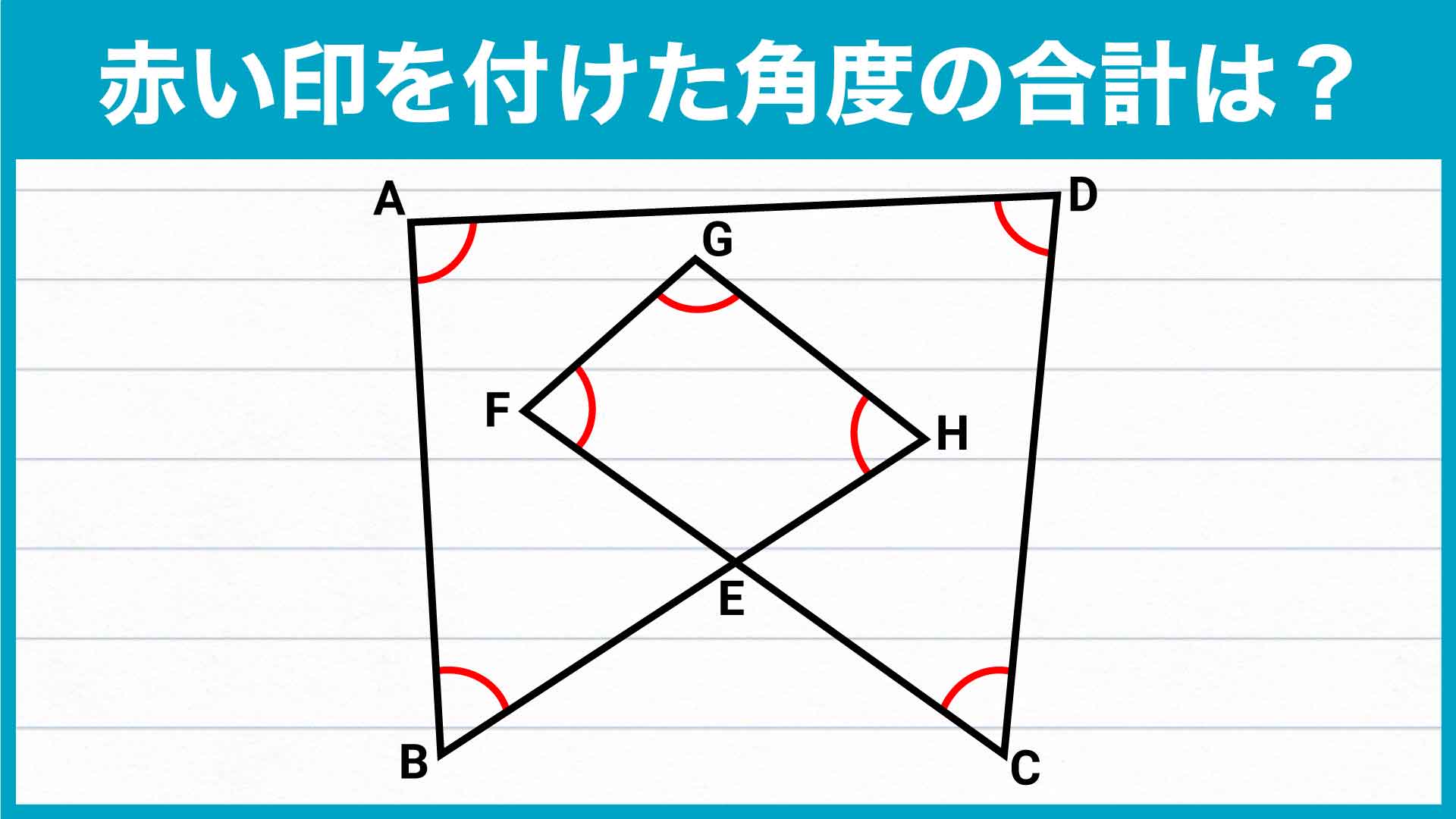
今回も僕と一緒に解いていきましょう! 具体的な角度がひとつもわかっていない状態から、どのように角度の合計を求めるのでしょうか……?
今回の問題でポイントとなるのが、「補助線を引いて、内角の合計が求めやすい三角形や四角形を見つけ出すこと」です。
ここで見つけた図形と赤い角の関係性から、赤い角の合計を求めていきます。
それでは、解説していきます!
ステップ1:補助線を引く
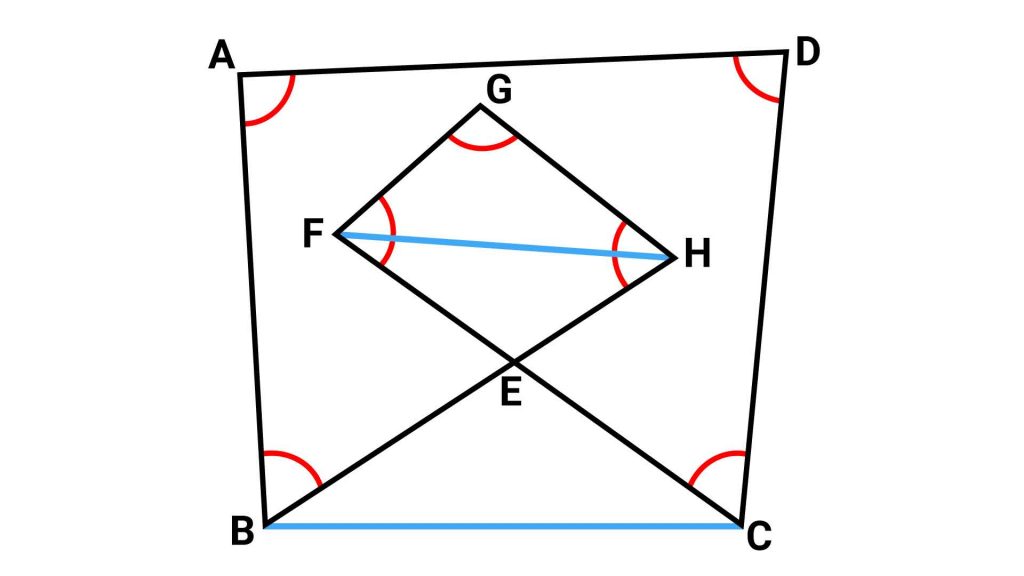
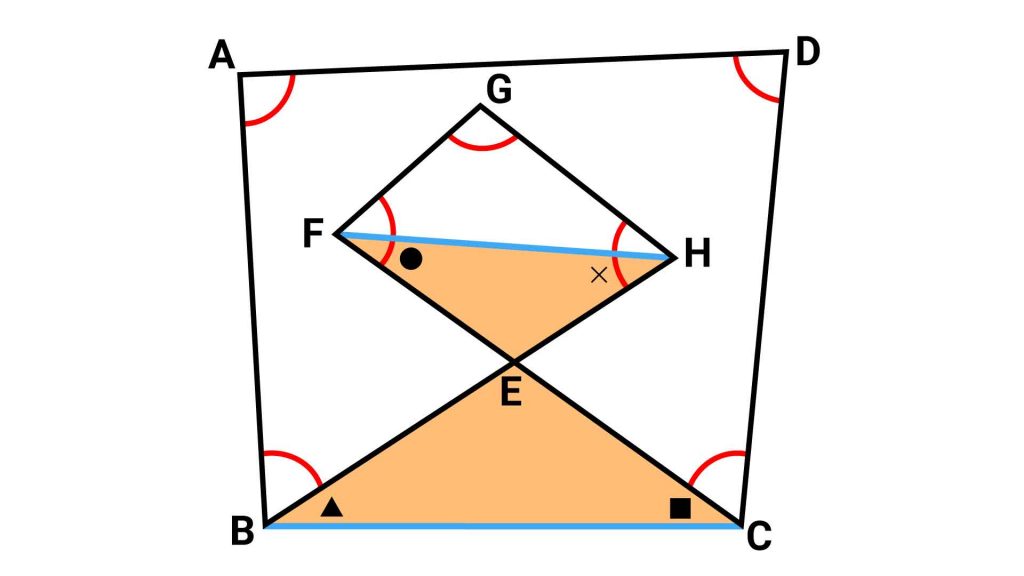
まずは以下のように、図形に2本の補助線を引きます。
補助線を引くことで、三角形FGHと四角形ABCDができました。これらの内角の合計は簡単に求めることができそうですね。
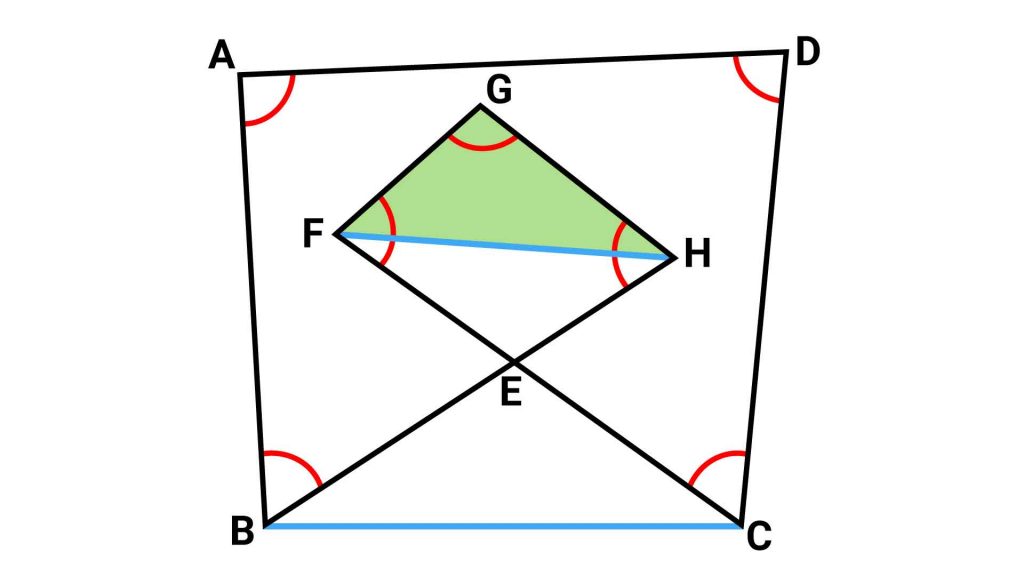
先に三角形FGHについて見ていきましょう。
三角形FGHの内角の和は180度なので、角GFH+角GHF+角FGH=180度となります。
中心の図形にある、赤い角が分割されているのが気になりますが、次のステップでスッキリ求めることができます。
ステップ2:残った赤い角を求める
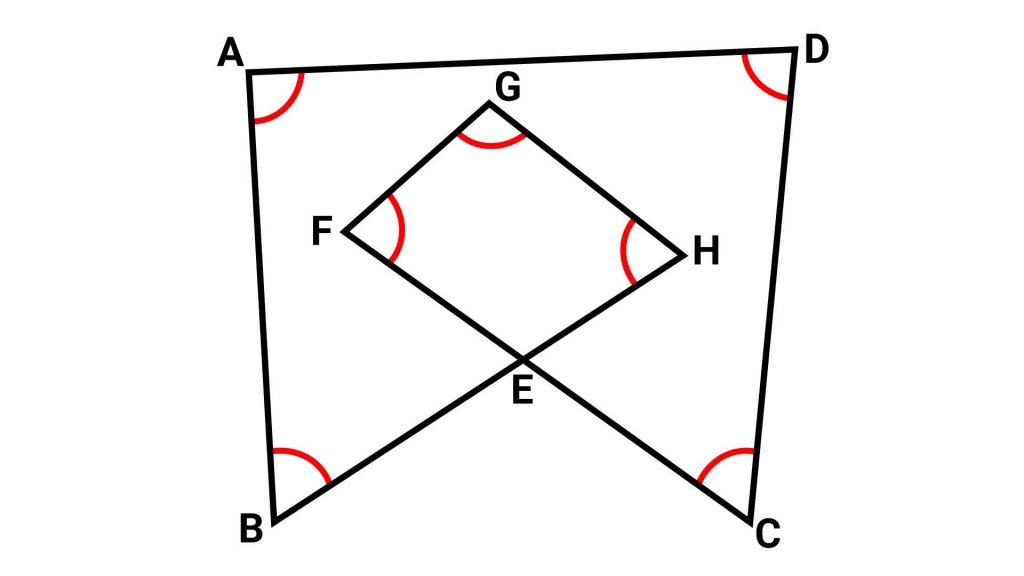
次に、残りの赤い角度について考えます。
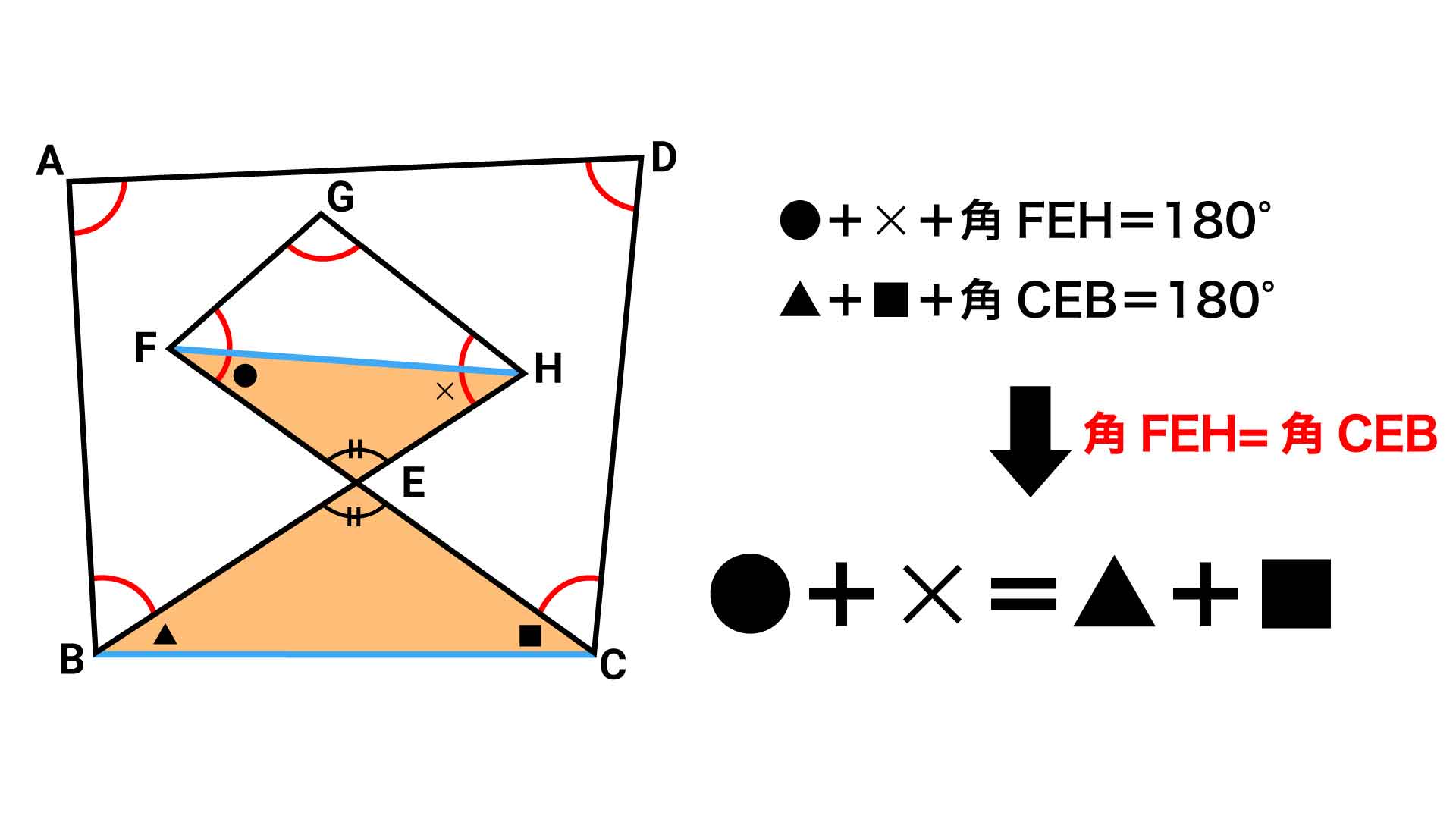
その角度を考えるにあたって着目するのは、向かい合う2つの三角形FEHとCEBです。
説明しやすいように、4つの角に●、×、▲、■の記号をつけました。
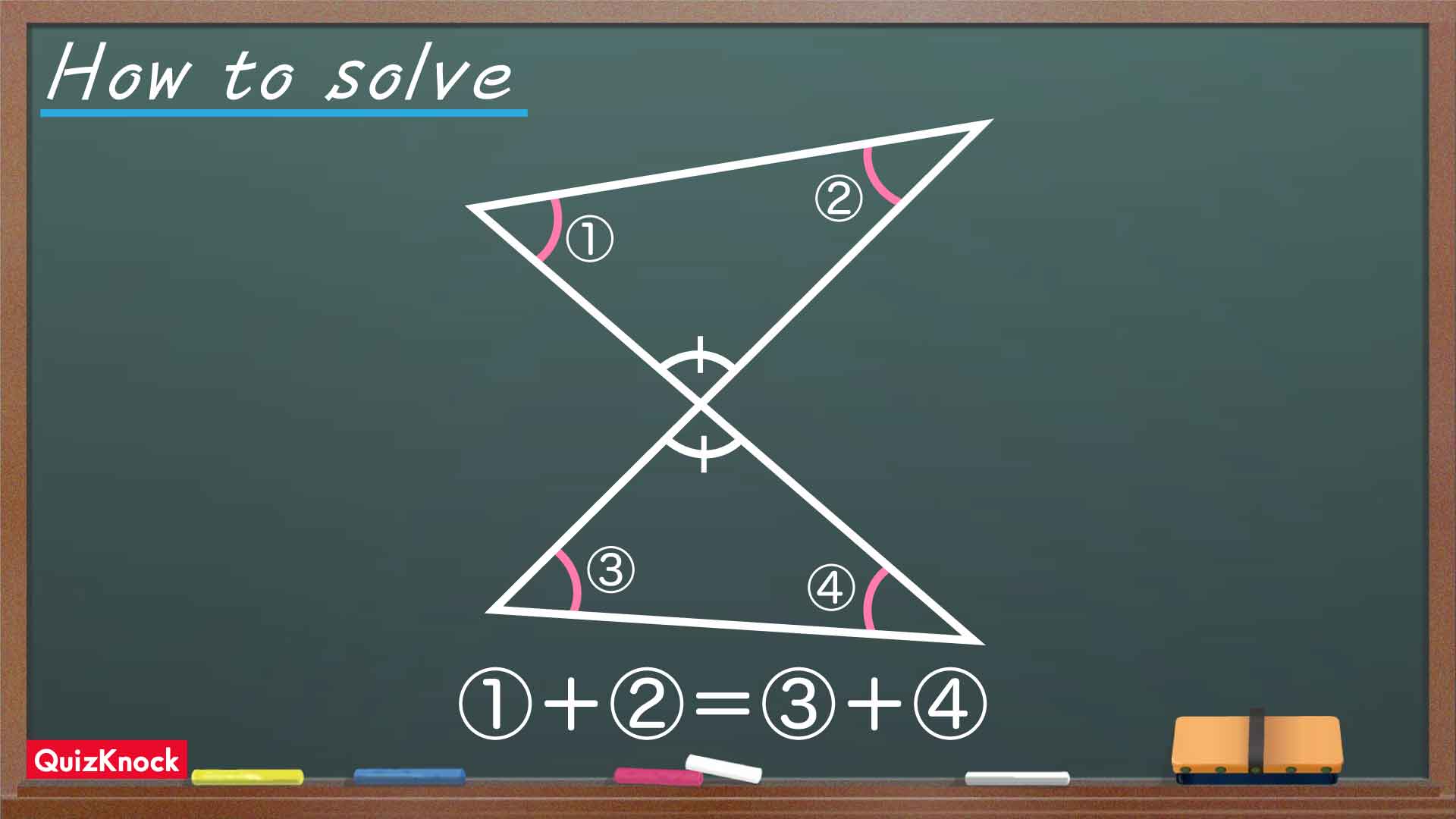
2つの直線が交わってできた、向かい合う2つの三角形の角度について、以下の重要な性質が成り立ちます。
この性質は、三角形の内角の和は180度であることと、2つの直線が交わるときに向かい合う角(対頂角)は等しいことに基づいて成り立っています。
この図形はよく「ちょうちょ型」や「リボン型」とよばれます。オリジナルの名前を付けて楽しんでみましょう!(僕は砂時計型)
この性質を先ほどの図形に落とし込むと、●+×=▲+■となります。
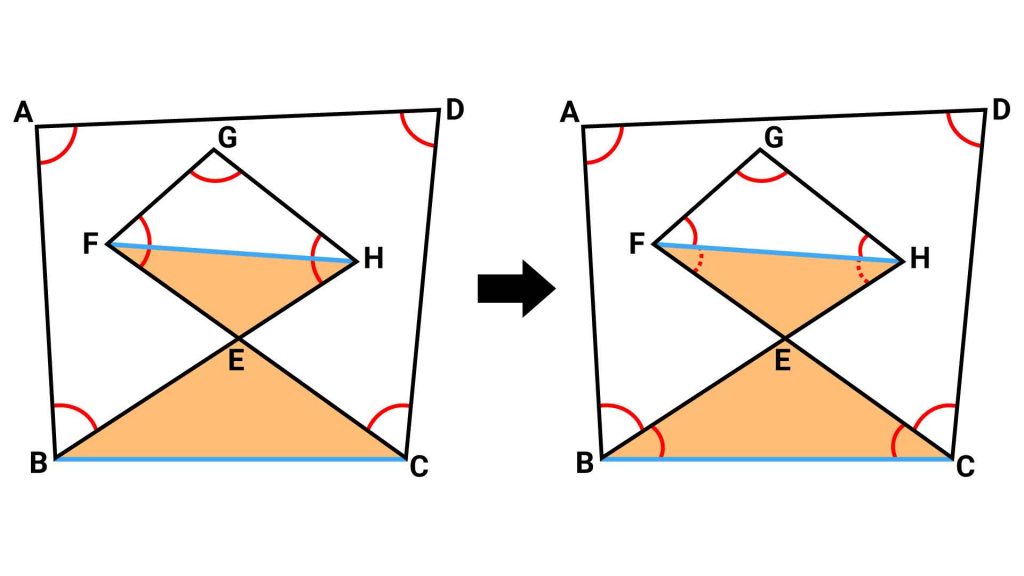
つまり、四角形GFEHの中にある残りの赤い角は、下の図のように置き換えることができます。
したがって残りの赤い角は、四角形の内角の合計(=360度)と等しくなります。
以上より、赤い角の合計は、180度+360度=540度となります。
答え:540度
具体的な角度がひとつも示されていなくても、答えを求めることができました!
補助線2本で三角形と四角形に分けられるかがポイントでした。
それでは。
【あわせて読みたい】










.jpg)







.jpg)






