小学5年生で解ける「図形の面積」の問題。あなたは解ける？

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

前ページ：【解答フォーム】自力で解きたい方はこちらへ！　以下は問題の答えです

今回の重要なポイントはこちらです。

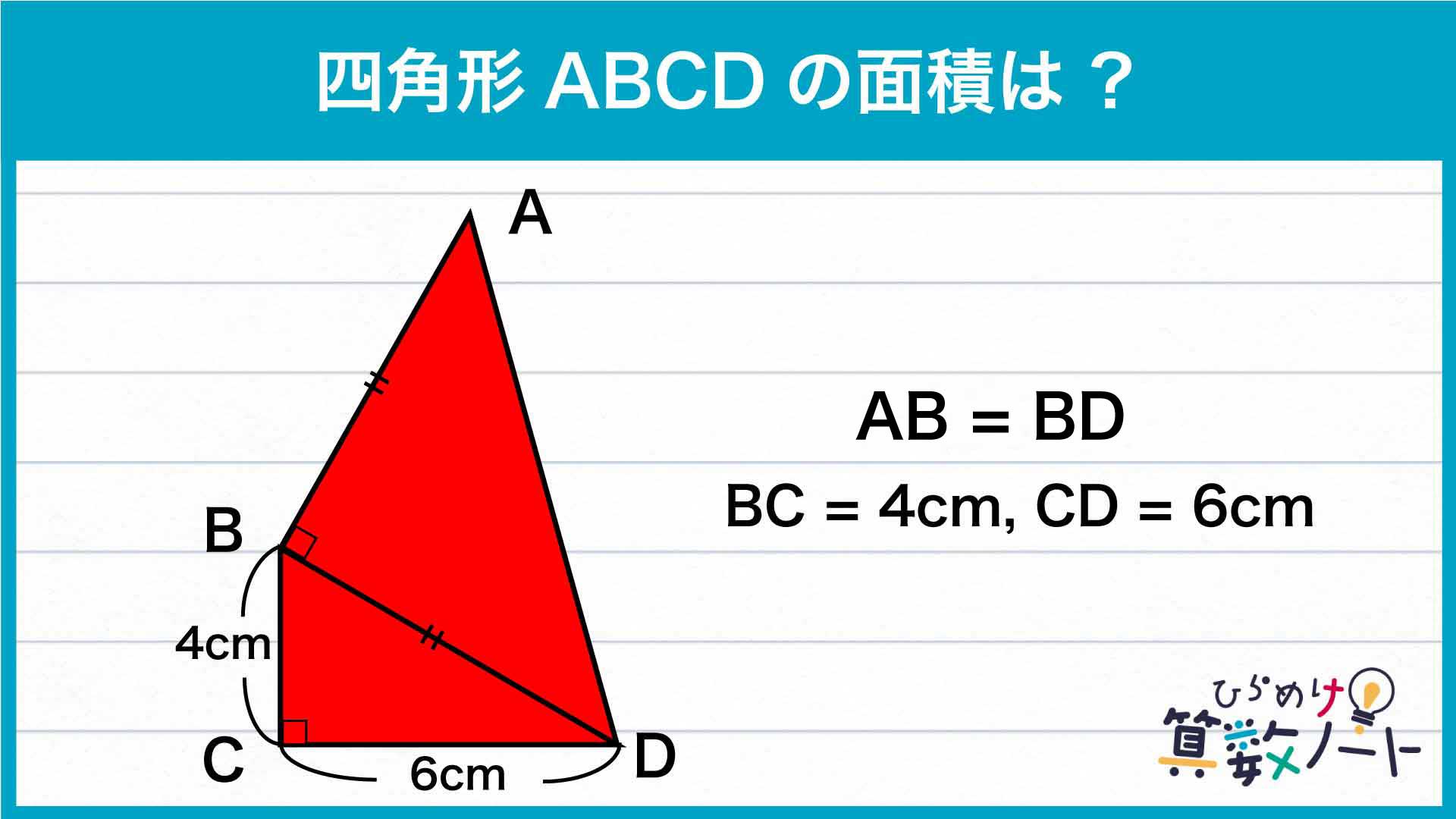
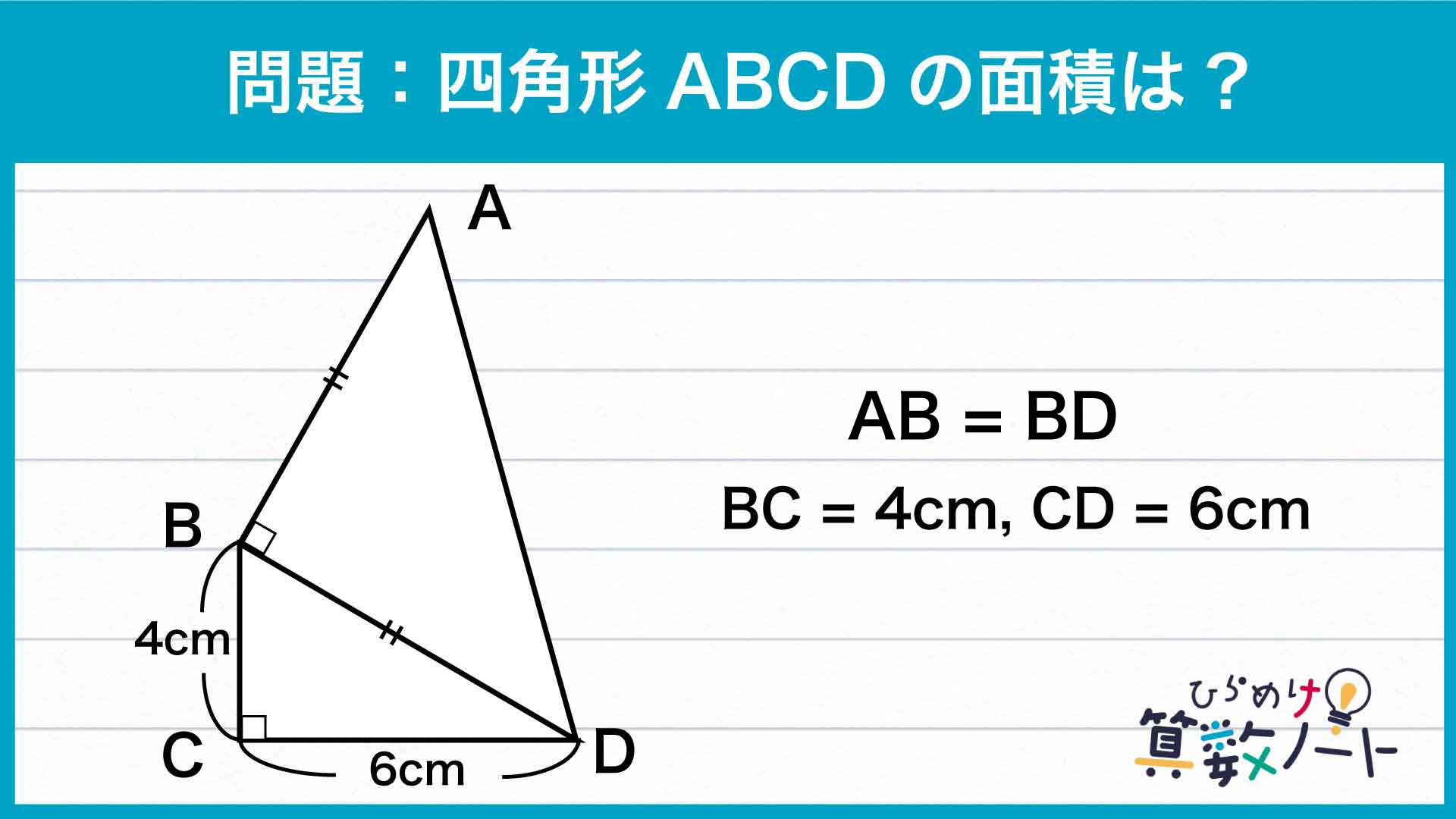
ポイントは、長さが同じ2本の辺に着目して、問題の図形に補助線を引き形が同じ三角形を付け足すことです。

三角形BCDと同じ三角形を付け足す

まずは、三角形ABDと三角形BCDが辺BDを共有していること、三角形ABDが二等辺直角三角形であることを用いて、補助線を引きます。

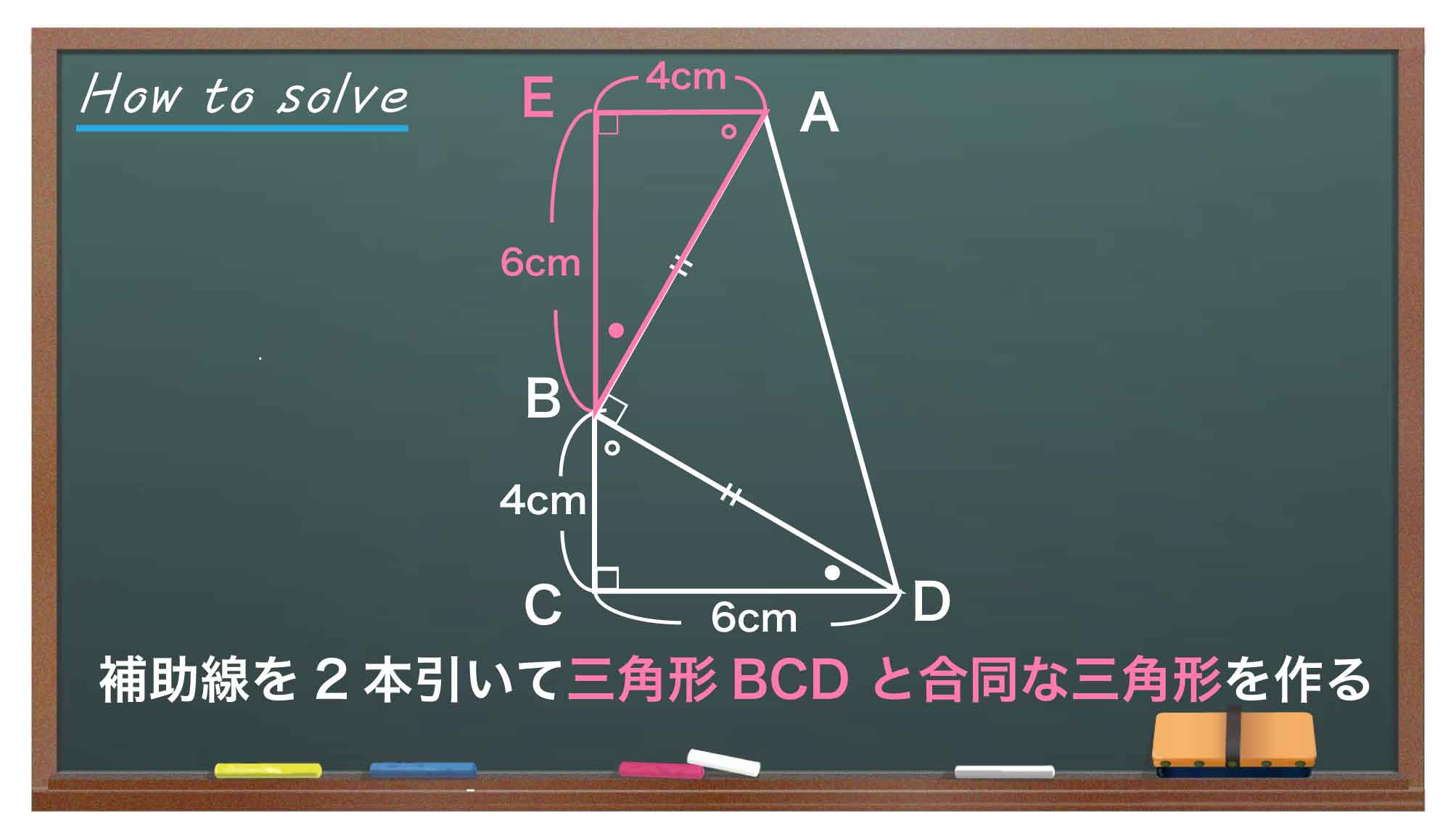
辺BDと辺ABの長さが等しいため、下の図のように、三角形BCDと同じ直角三角形を辺ABに付け足すことができます。この三角形を三角形AEBとします。

角CBDを白い丸、角BDCを黒い丸と置いたとき、角ABEが黒い丸に、角EABが白い丸に対応します。

四角形AECDの形を調べる

足した三角形AEBが、四角形ABCDにどのように接しているかを調べます。

まずは、CBEの角度についてです。三角形の内角の和は180度なので、白い丸と黒い丸の和は90度となります。CBEの大きさは白い丸、黒い丸、直角の和なので90+90=180度とわかります。よってCBEは直線です。

また、角DCEと角CEAは共に90度なので、辺EAと辺CDは平行であることもわかります。よって、四角形AECDは台形であることがわかります。

四角形AECDの面積から答えの面積を求める

求めたい四角形ABCDの面積は、四角形AECDの面積から三角形ABEの面積を引くことで得られます。

四角形AECDは上底が4cm、下底が6cm、高さが6+4=10cmの台形なので、面積は(4+6)×10÷2＝50cm²となります。また、三角形ABEの面積は6×4÷2＝12cm²となります。よって、四角形ABCDの面積は50-12=38cm²となります。

答え：38cm²

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】