小学6年生で解ける「円の面積」の問題に挑戦！あなたは解けますか？

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

前ページ：【解答フォーム】自力で解きたい方はこちらへ！　以下は問題の答えです

今回の問題の解き方をまとめた図がこちらです。ポイントは円の内部にある直角二等辺三角形に着目することです。

このポイントをもとに、解いていきましょう！

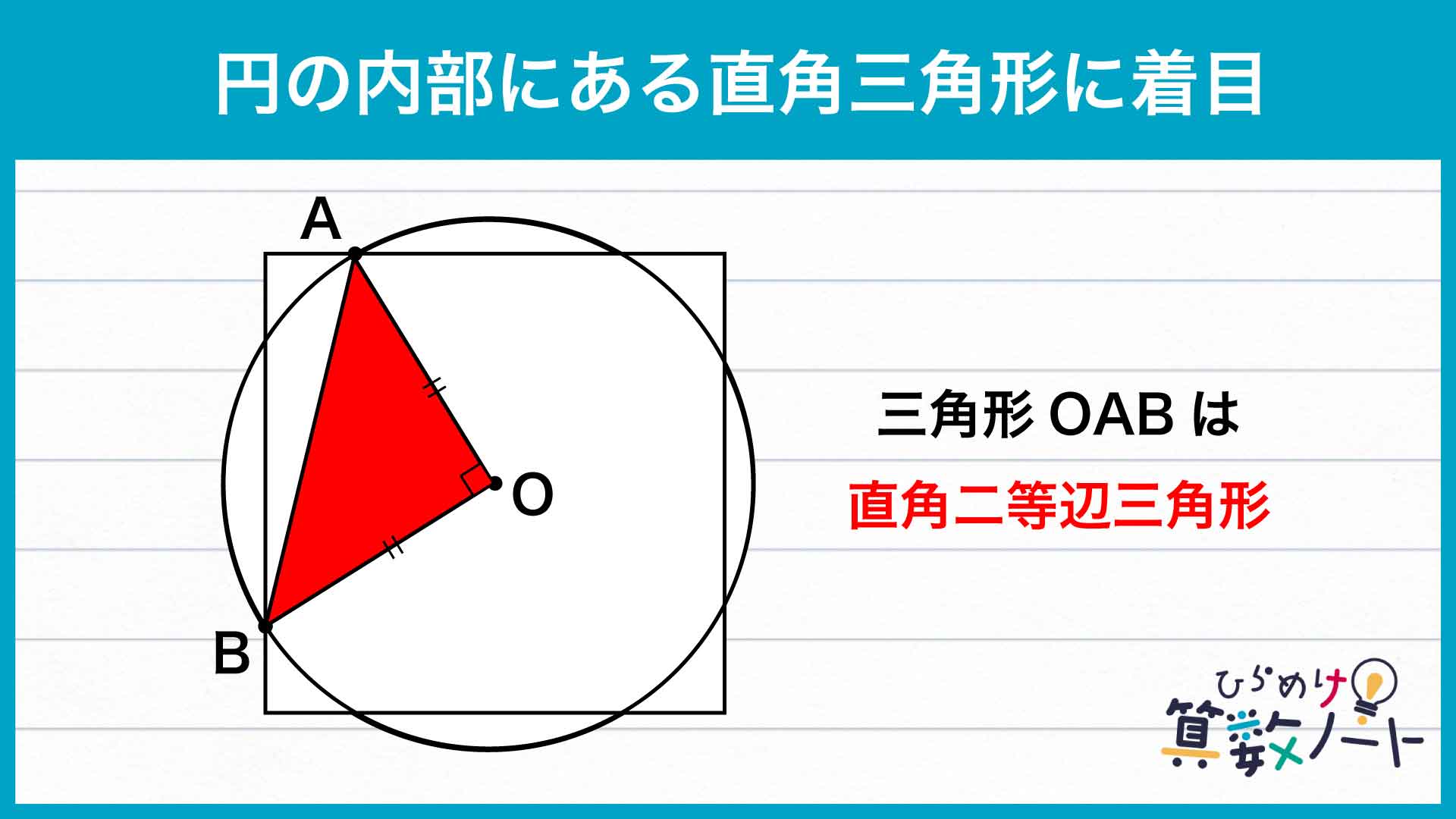
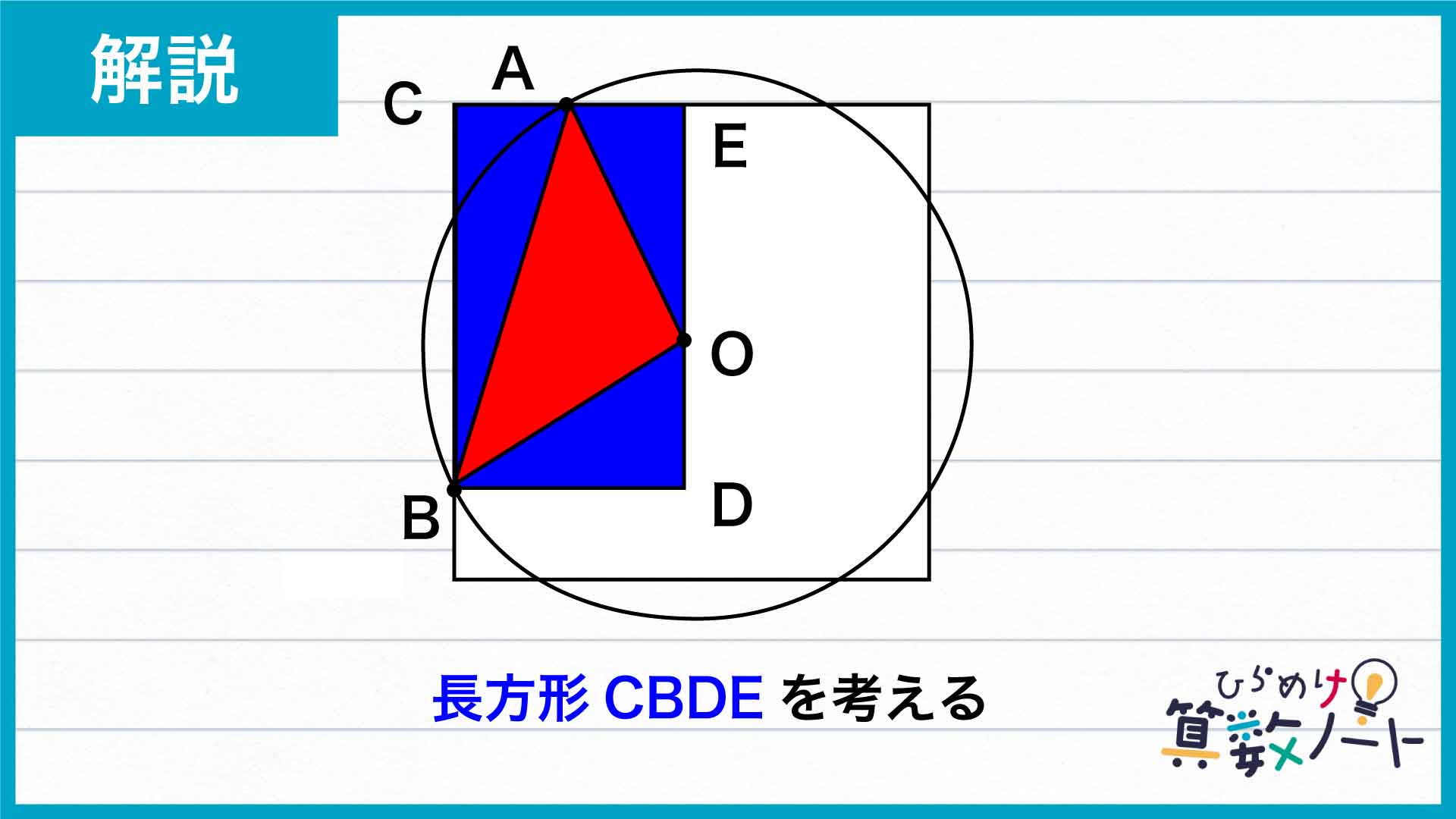
円の中の直角二等辺三角形

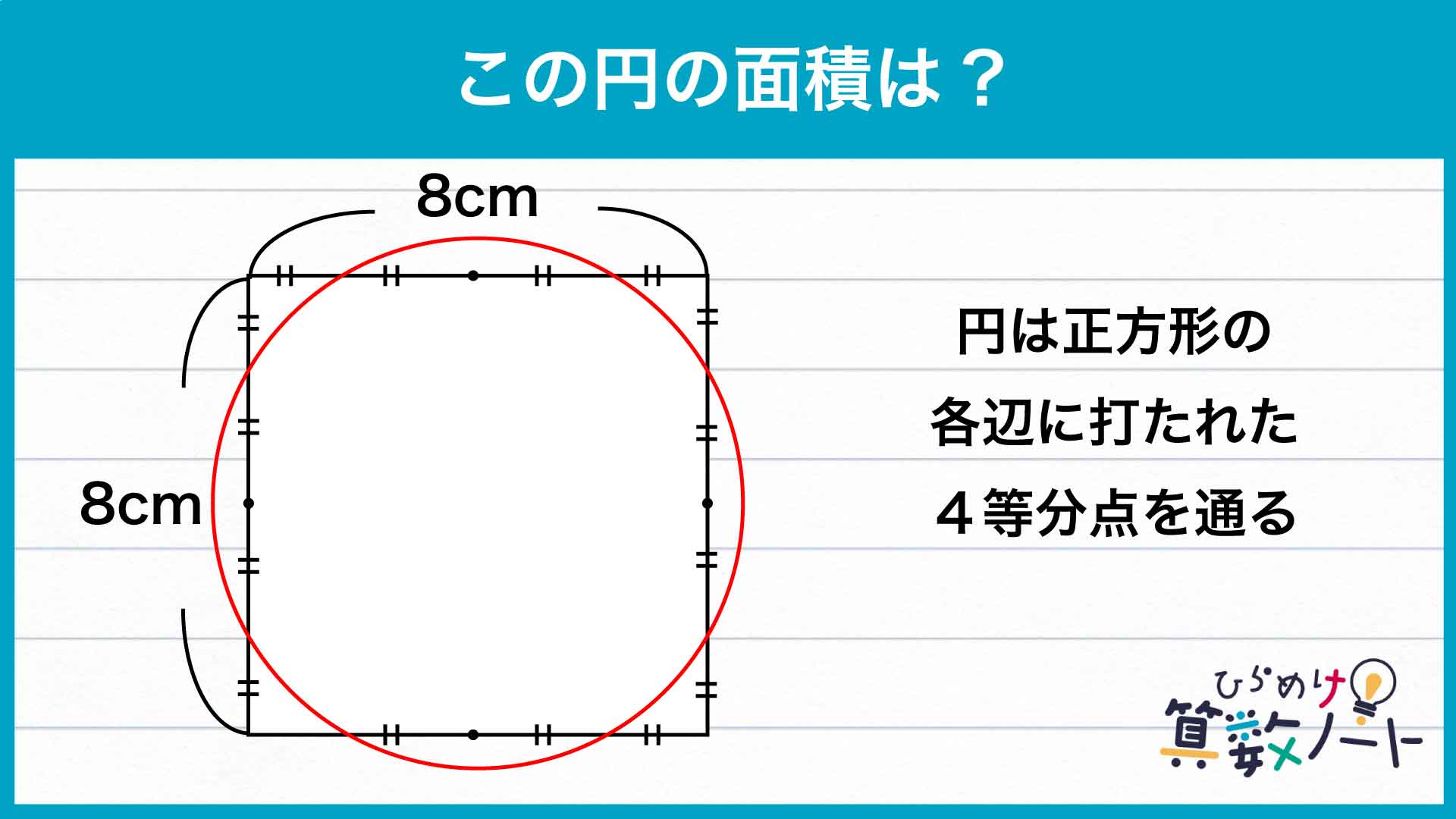
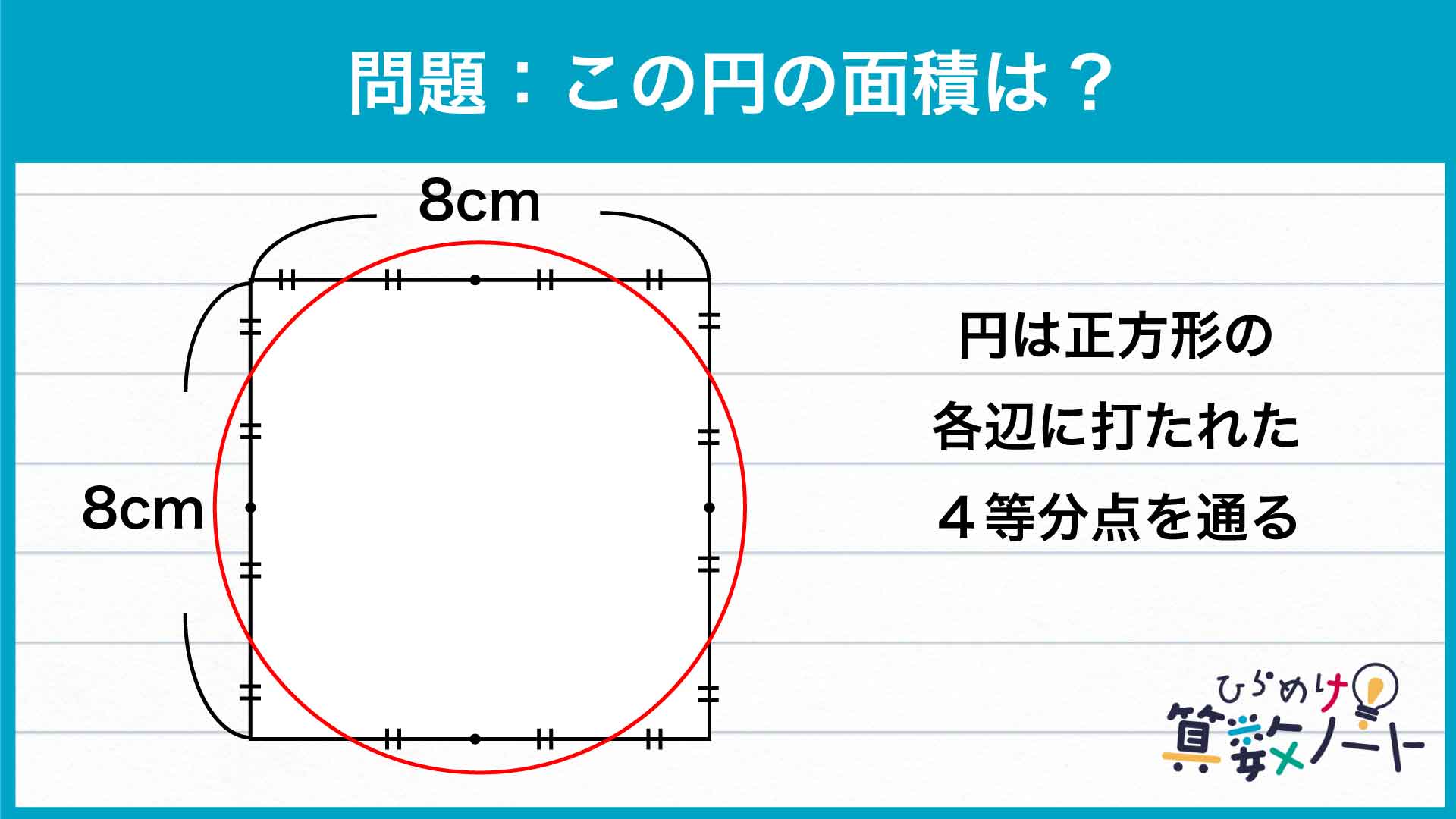
下の図のように円を4つの扇おうぎ形に4等分すると、それぞれの扇形の中心角は360÷4=90度となります。

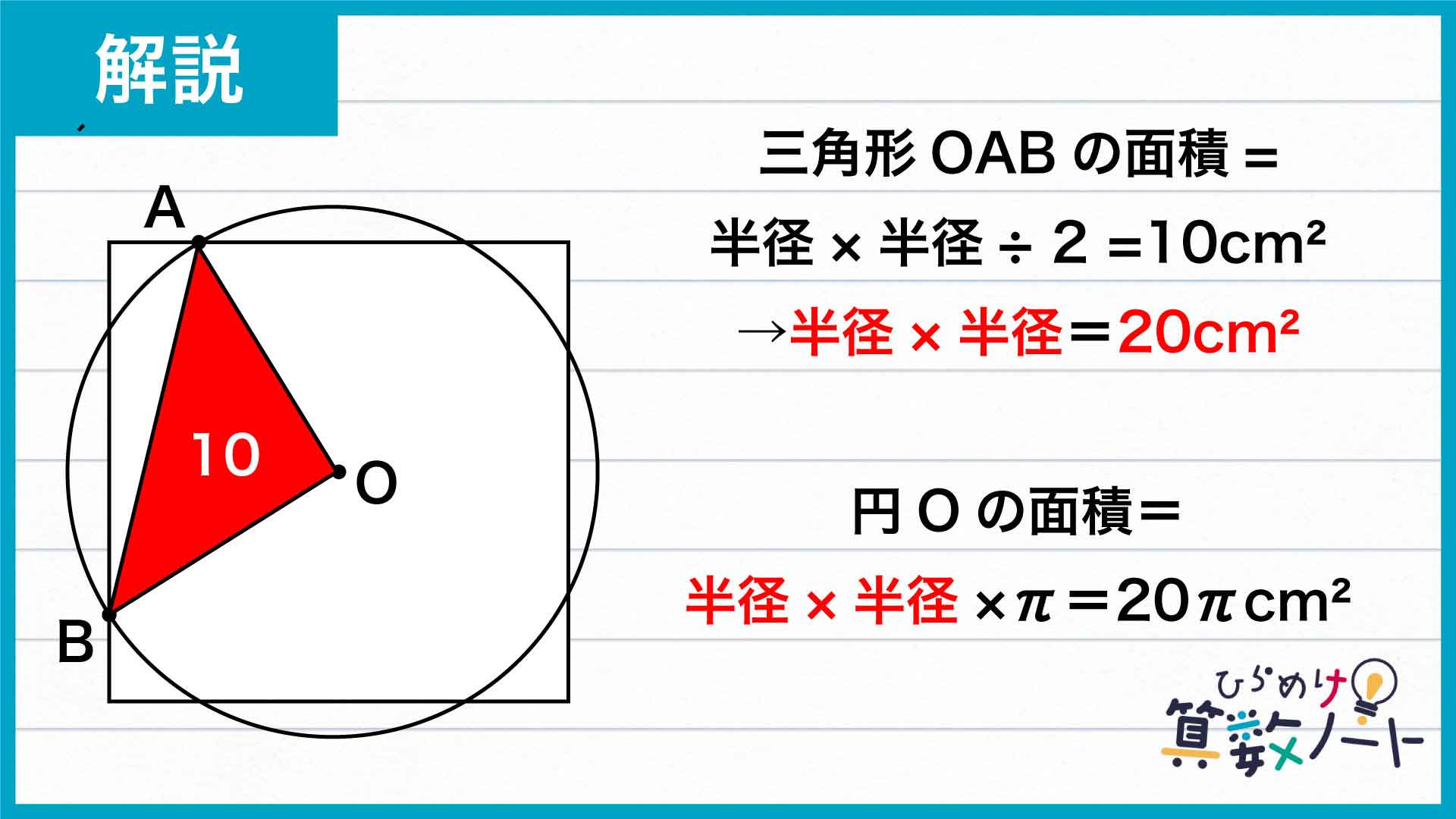
下の図のように三角形OABに着目すると、角AOBは90度で、OAとOBはともに円Oの半径です。このことから、三角形OABは、OA=OBの直角二等辺三角形であることがわかります。

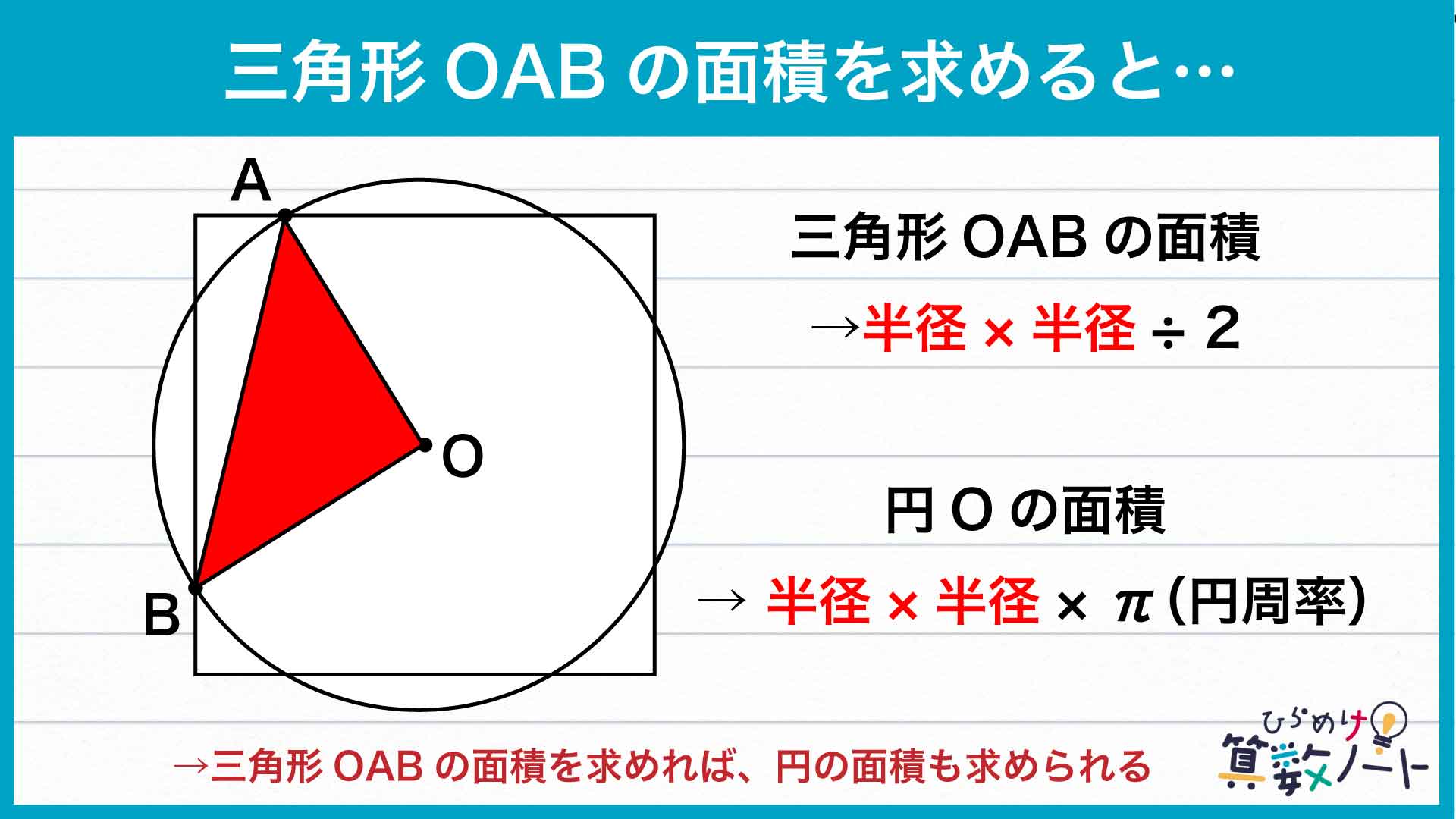
三角形OABの面積は、OA×OB÷2で求められます。OA、OBは円Oの半径でもあるので、三角形OABの面積は、半径×半径÷2と表すこともできます。

一方、円Oの面積は、半径×半径×πで求められます。

三角形OABの面積がわかれば、半径×半径の値がわかるので、円の面積を求めることができます。

直角二等辺三角形OABの面積は？

三角形OABの各辺の長さは、小学生の算数の範囲では直接求めることができません。

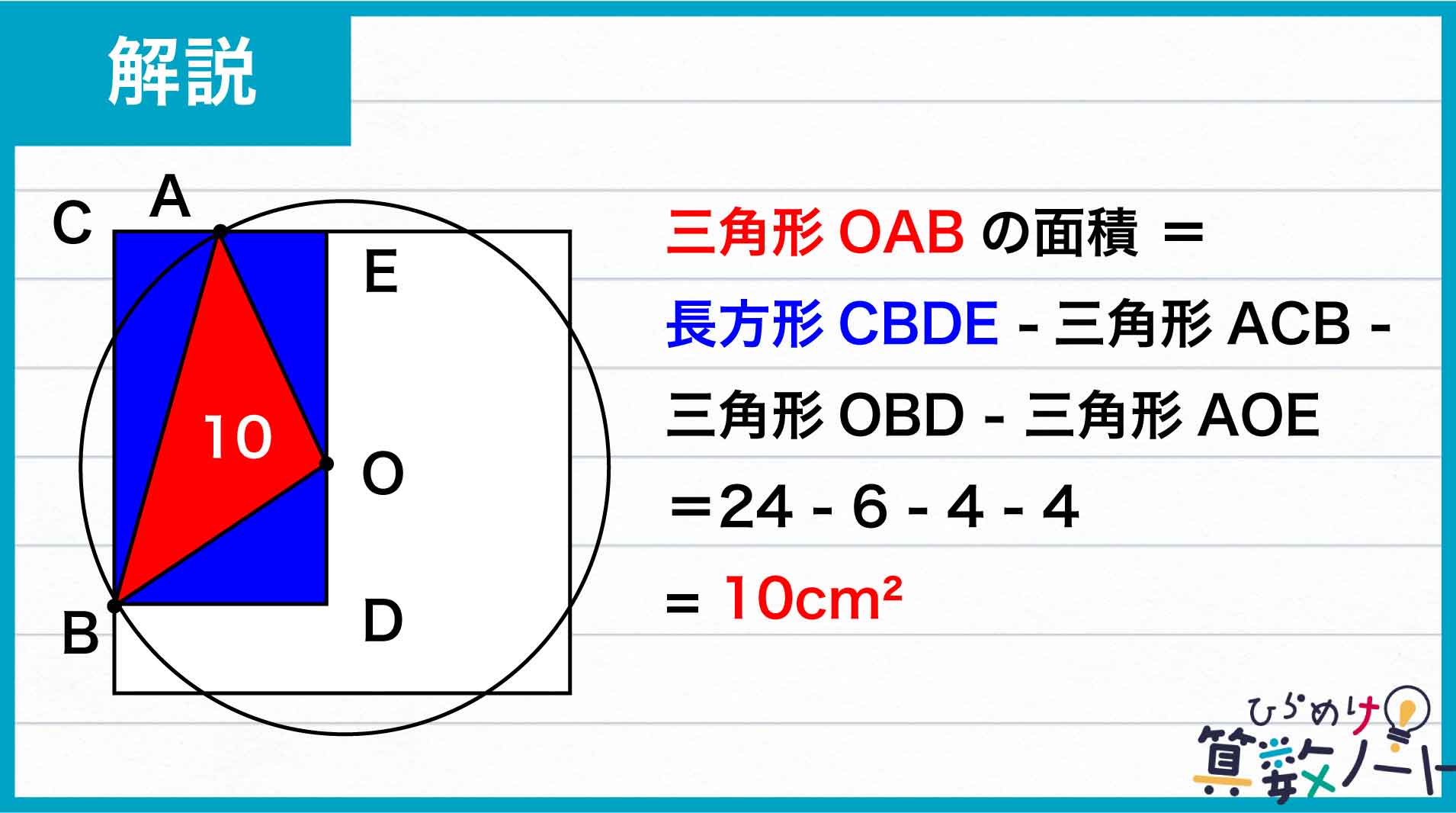
そこで、下の図のような長方形CBDEを考えることで、間接的に三角形OABの面積を求めていきます。三角形OABの面積は、長方形CBDEの面積から、三角形ACB、三角形OBD、三角形AOEの面積を引くことで求めることができます。

A、Bが共に正方形の一辺の4等分点、Eが正方形の一辺の中点であることなどを踏まえると、AC=2cm、CB=6cm、CE=BD=4cm、OE=4cm、OD=2cmです。

したがって、長方形CBDEの面積は6×4=24cm²、三角形ACBの面積は6×2÷2=6cm²、三角形OBDの面積は4×2÷2=4cm²、三角形AOEの面積は4×2÷2=4cm²とそれぞれ求められるため、三角形OABの面積は、24-6-4-4=10cm²となります。

あと一歩！

三角形OABの面積は、半径×半径÷2と表すことができ、これが10cm²であることから、半径×半径は20cm²であることがわかります。

したがって、円Oの面積は、半径×半径×π=20πcm²です。

答え：20πcm²

「ひらめけ！算数ノート」のバックナンバーはこちら！

【前回の算数ノートはこちら】

【あわせて読みたい】