ヒント
下の図のように円を4つの
下の図の三角形OABに着目してみましょう。
ABを弧とする扇形の中心角が90度であり、OAとOBはともに円Oの半径であることから、三角形OABは直角二等辺三角形であることがわかります。
したがって、三角形OABの面積は、OA×OB÷2、すなわち、(円の半径)×(円の半径)÷2で求めることができます。
円Oの面積は、(円の半径)×(円の半径)×π(円周率)で求められるので、三角形OABの面積がわかれば、円の面積も求められそうです。
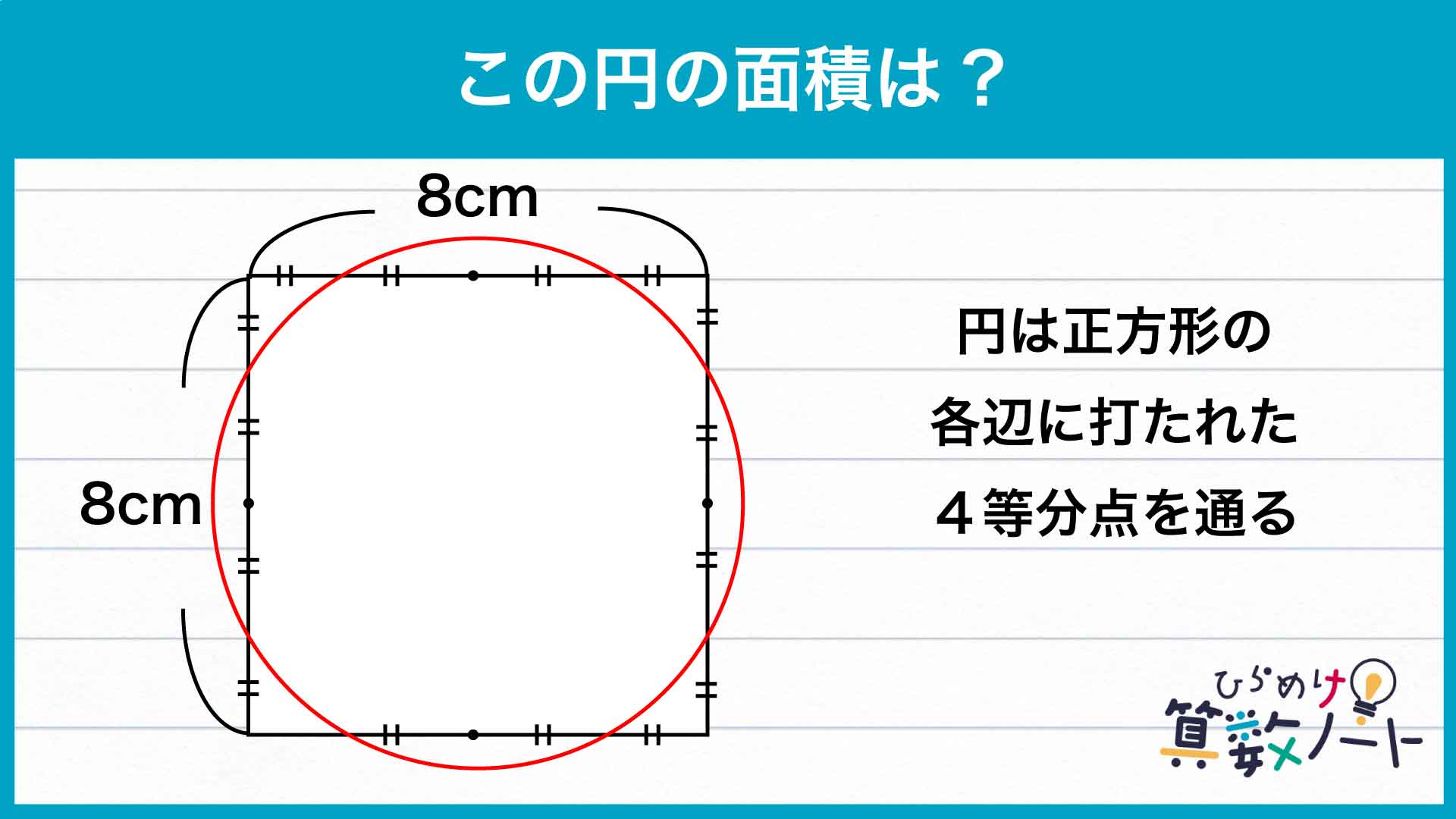
下の図のように円を4つの
下の図の三角形OABに着目してみましょう。
ABを弧とする扇形の中心角が90度であり、OAとOBはともに円Oの半径であることから、三角形OABは直角二等辺三角形であることがわかります。
したがって、三角形OABの面積は、OA×OB÷2、すなわち、(円の半径)×(円の半径)÷2で求めることができます。
円Oの面積は、(円の半径)×(円の半径)×π(円周率)で求められるので、三角形OABの面積がわかれば、円の面積も求められそうです。

伊東
東京大学大学院修士課程修了(工学)。クイズはもちろんのこと、スポーツ、みかんも好きです。よろしくお願いします。