解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
問題の解き方をまとめた図がこちらです。
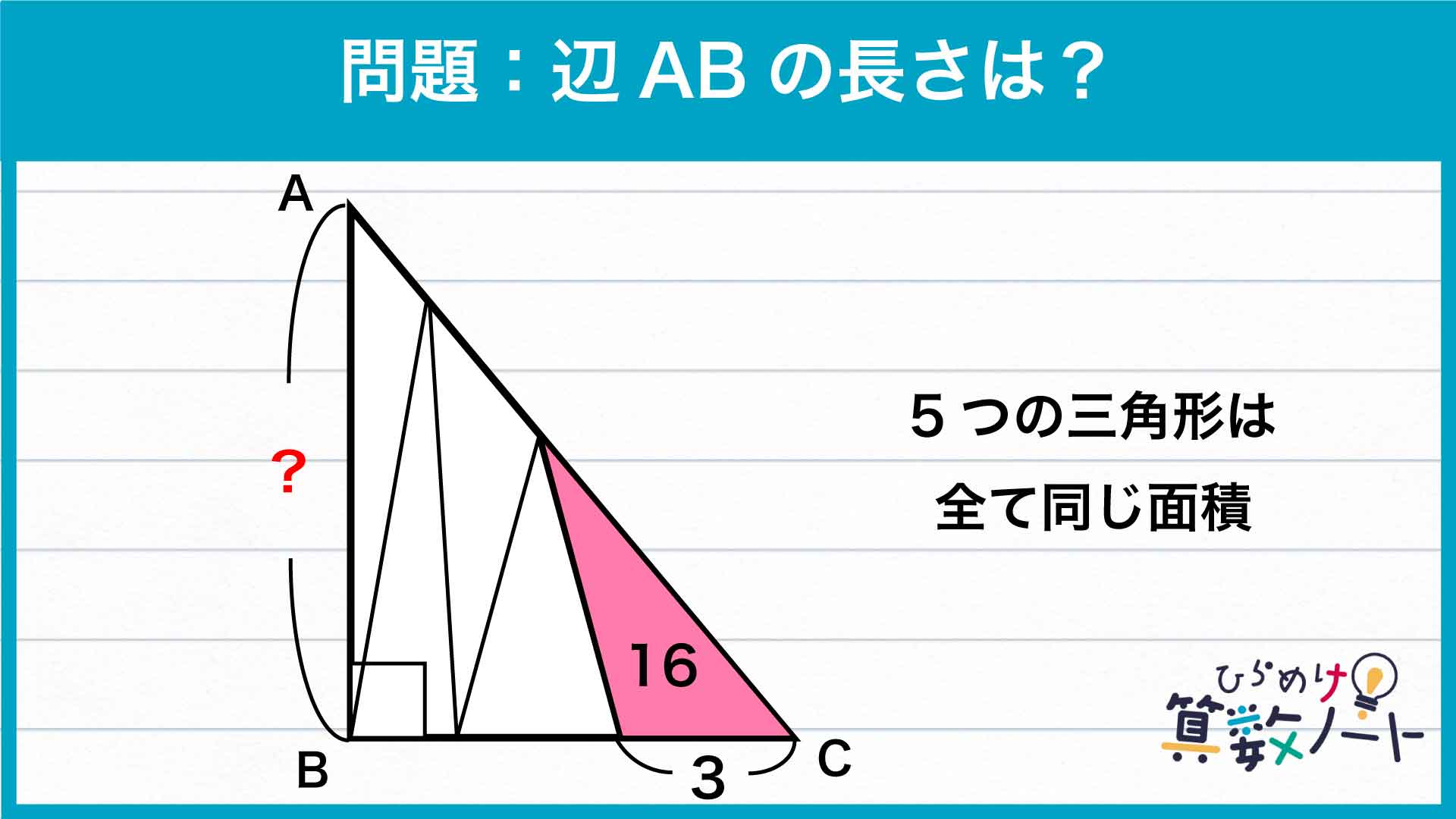
ポイントは、高さが等しい三角形の面積比を利用して、辺BCの長さを求めることです。
では、このポイントを踏まえつつ解いていきましょう!
辺BCの長さを求める
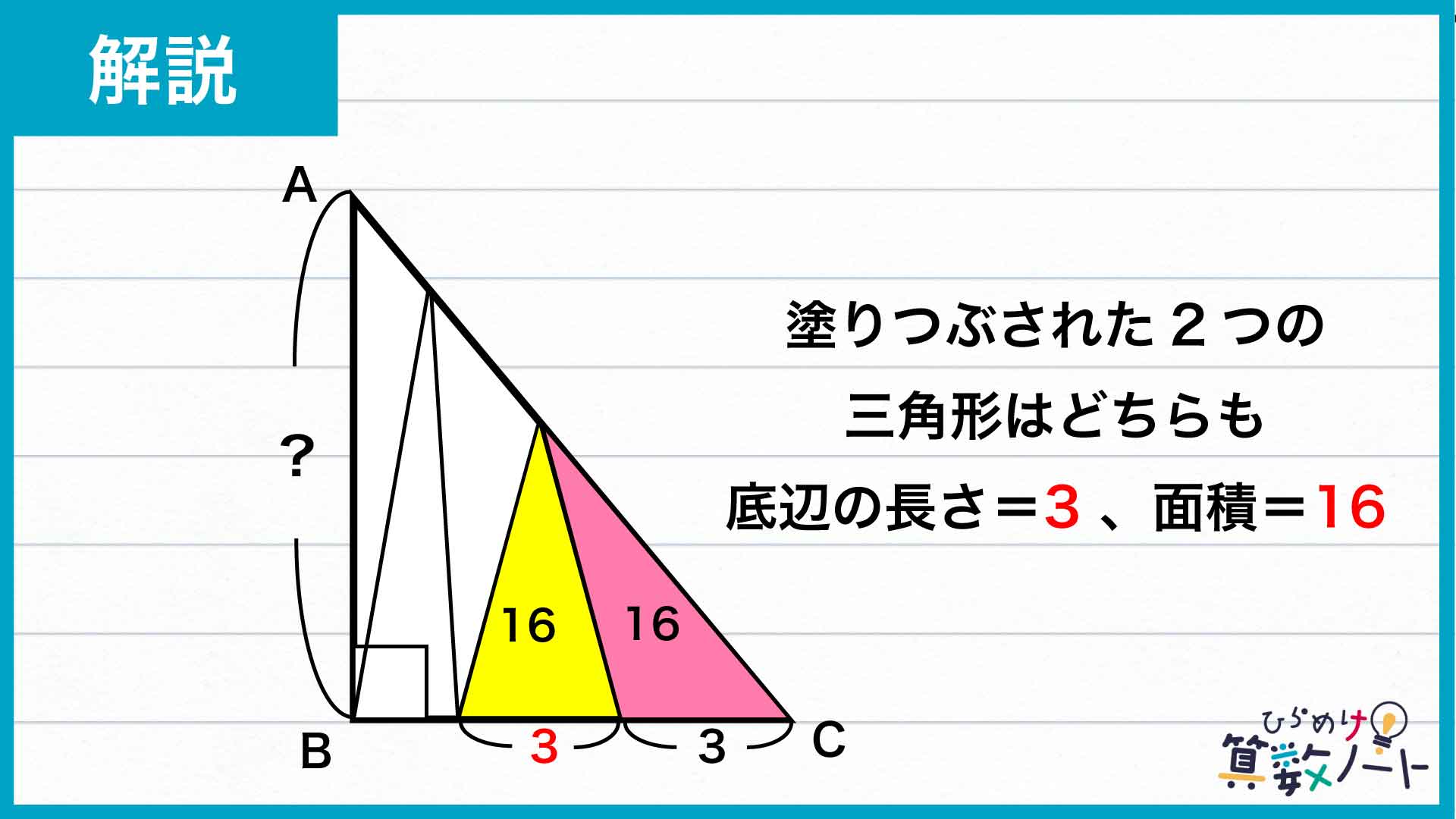
まずは、下の図で塗りつぶされた2つの三角形に注目します。2つの三角形は面積と高さが等しいことから、底辺の長さも等しくなります。したがって、左側の三角形も底辺の長さが3であるとわかります。
辺BCの残りの部分についても、同じようにして長さを求めます。今度は下の図に示した2つの三角形に注目してみましょう。含まれている三角形の個数から、面積の比は1:3です。この2つの三角形もまた高さが等しいので、底辺の長さの比は1:3となります。したがって、辺BCの残りの部分は長さが(3+3)÷3=2であるとわかるのです。
辺ABの長さを求める
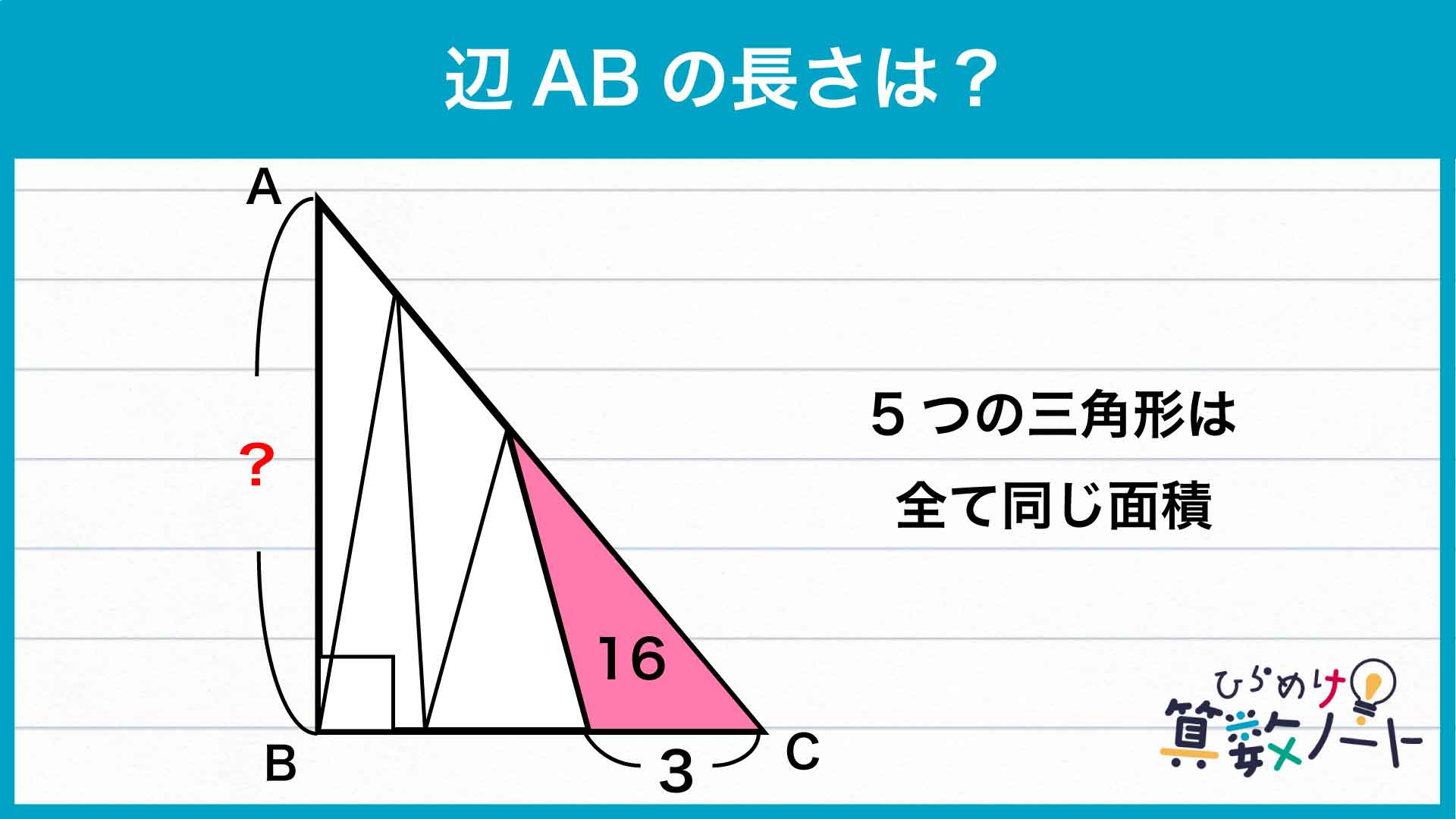
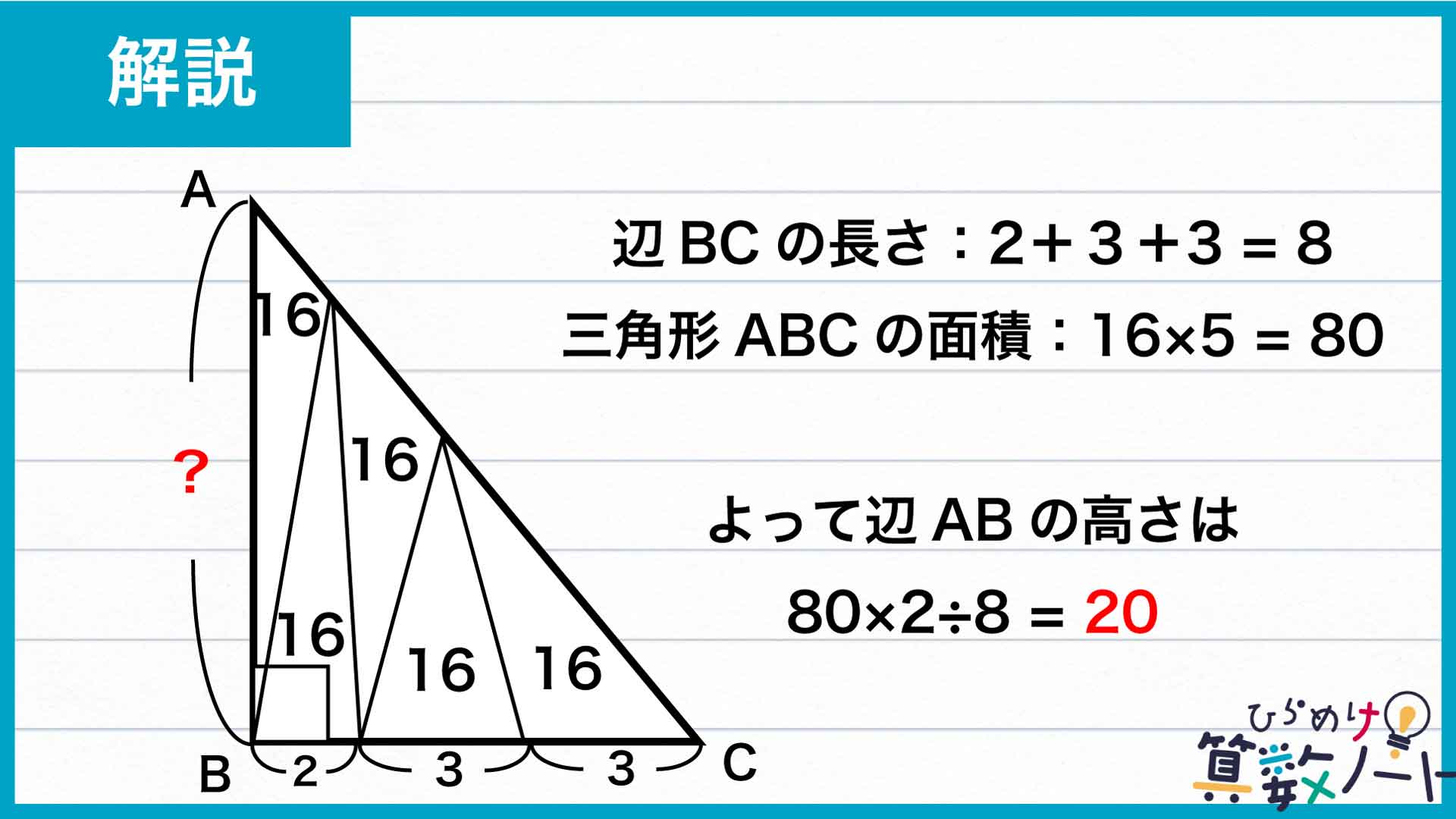
以上のことから、辺BCの長さは2+3+3=8であるとわかります。また、三角形ABCは面積16の三角形5個が集まったものなので、その面積は16×5=80。三角形の面積は「底辺×高さ÷2」で表すことができるため、辺BCを底辺としたときの高さにあたる辺ABの長さは80×2÷8=20となるのです。
答え:20
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】











.jpg)










.jpg)







