コジマです。
以前、肉眼でも読める！QRコード入門という記事を書いたことがあり、大きな反響をいただいた。
QRコードは正方形の領域にデータを詰め込んだ2次元コードであり、横一列に白黒のパターンを並べたバーコードよりも多くの情報を表せる。
つまり、バーコードはQRコードよりも簡単に読めるはずであり、QRコードが肉眼で読めるんだから（？）バーコードを読むなんてどうってことないはずだ。
肉眼で読んでやろうじゃないか、バーコードを！
基本用語「ガードパターン」「モジュール」
実はバーコードにもいろいろな種類があるが、ここでは最も一般的な、商品の識別に用いられているJANコードを読んでみることにする。
多くの場合、商品には13桁の数字がJANコードで表示されている（場合によっては8桁の短縮コードが用いられていることもある）。
ガードバターン
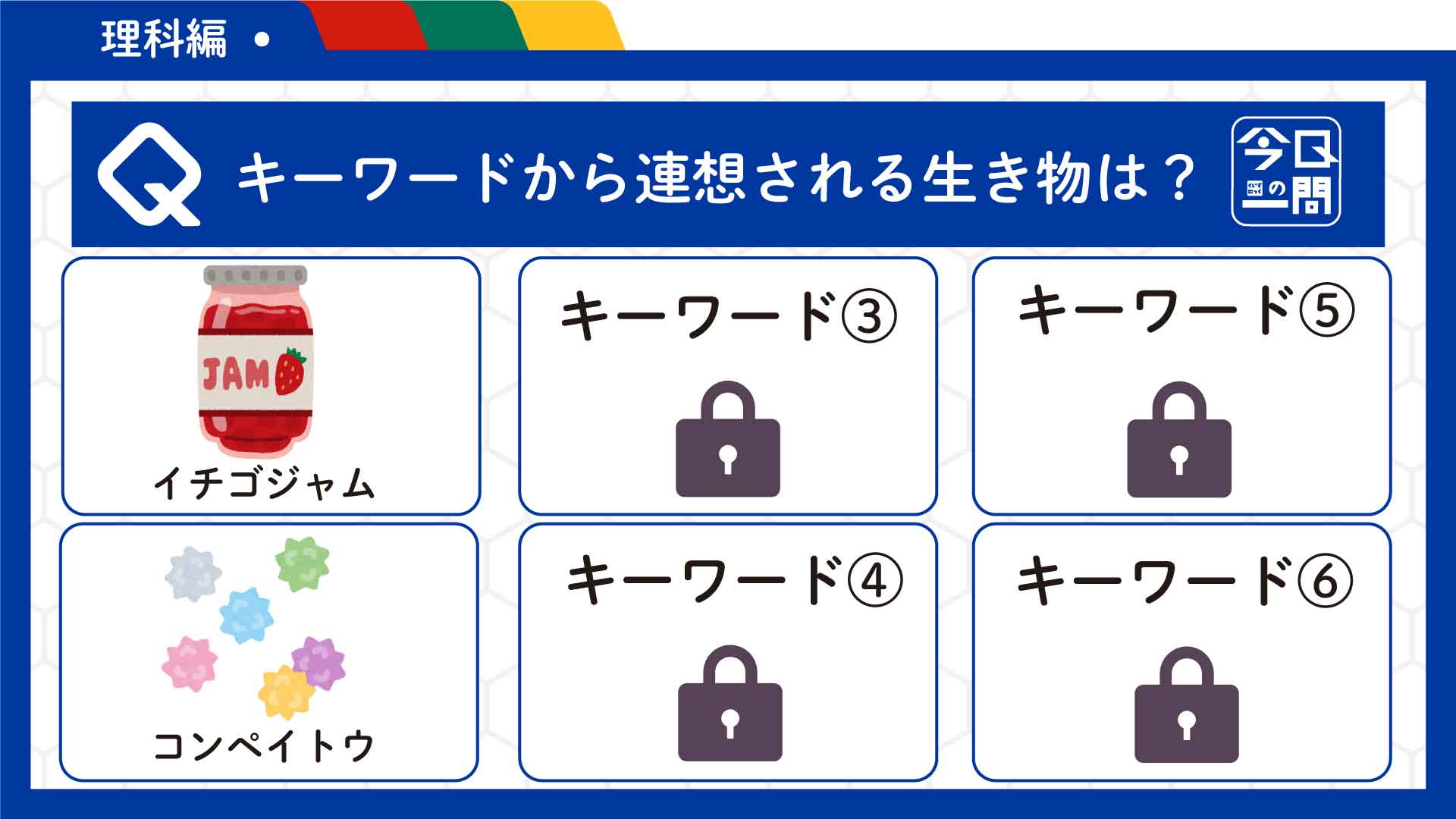
バーコードを眺めてみると、左右と中央の3箇所に他よりも線が長くなっている部分があることがわかる。これをガードパターンという。中央のガードパターンを境として、左側で6桁、右側でも6桁の数字を表す。
左右は3モジュール分、中央は5モジュール分がガードパターンとなっているモジュール
バーコードは線の幅が重要であり、最も細い幅（これを1モジュールと呼ぶ）を基準として7モジュールで1つの数字を表す。つまり、ガードパターンとガードパターンの間には7×6=42モジュール分の線が描かれていることになる。
バーコードを左から7モジュールずつ区切っていくと、必ず黒い線と白い線がそれぞれ2本ずつ含まれていることが分かるはずだ。白黒白黒の4つの領域の幅を読み取って、対応表から数字を復元していくことになる。
7モジュールごとに区切った領域（青と緑）をよく見ると、必ず白と黒の線が2本ずつ含まれることが分かる浮いたアイツにも意味がある
ここで対応表を……といきたいところだが、ここまでの説明で矛盾する点がある。JANコードは13桁の数字なのに、6桁+6桁だと12桁しかないじゃん！
一番左の数字は特別
今まで生きてきて気になっていた人も多いんじゃないだろうか、数字の一番左にいるちょっと浮いたコイツ。実はこの13桁の先頭1桁は、他の12桁とは少し違った表し方をされているのだ。
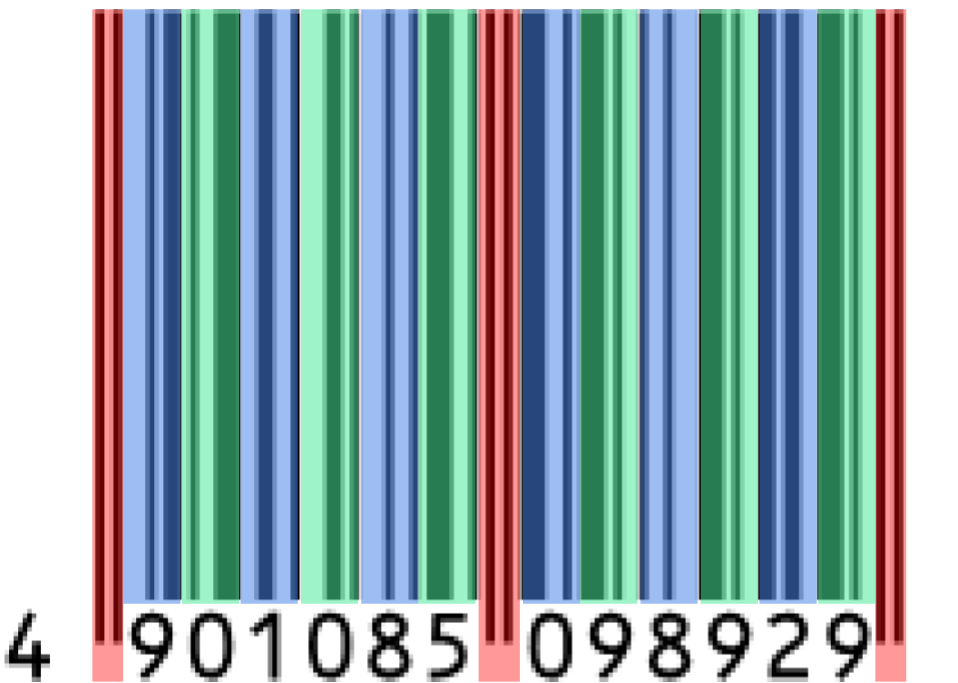
コイツ左半分を7モジュールずつ区切った6ブロックについて、それぞれの黒の幅を足し合わせ、合計が奇数か偶数かを判定する。例えば、白黒白黒の線の並びのブロックで、それぞれの幅が3, 2, 1, 1であれば、黒の幅は2と1なので、和の3は奇数。
そして、黒が奇数モジュール分あるところをA、偶数モジュール分あるところをBとすれば、ABAABBのようにAとBの並びができる。この並びを読み取って、以下の対応表から先頭の1桁を決めるのだ。
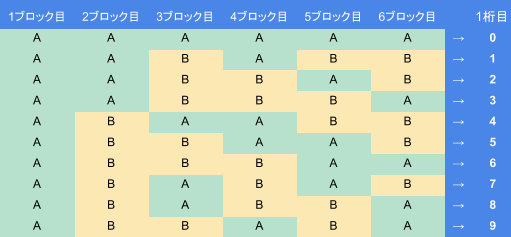
ちなみに、JANコードの最初の2桁は国コードで、日本ならば45か49と決まっている。つまり日本国内で買った商品のバーコードであれば、ほとんど4：ABAABBのパターンで並んでいると思って間違いない。
対応表さえあれば簡単！
さて、話を元に戻して、各ブロックを数字に変換するための表を示す。左半分と右半分、さらに左半分は黒のモジュール数の偶奇でパターンが変化するので、数字に対して3通りの表し方が存在する。
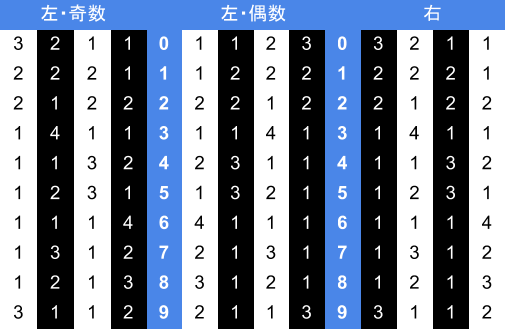左半分にあって、2（黒）,2（白）,1（黒）, 2（白）であれば、黒のモジュールは合計4なので、このブロックは表の真ん中を見ることになり、対応する数字は「2」白と黒の幅を読み取って、その並びを表に対応させるだけで、バーコードの中身が読み取れる。簡単！
こたえあわせ
ただし、残念ながらバーコードからデータを読み取るメリットはQRコードに比べて少ない。なぜなら普通はコードの下に数字が書いてあるから……。
バーコードを読んだ答え合わせは下のこれを読めばできる……本末転倒！
