解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
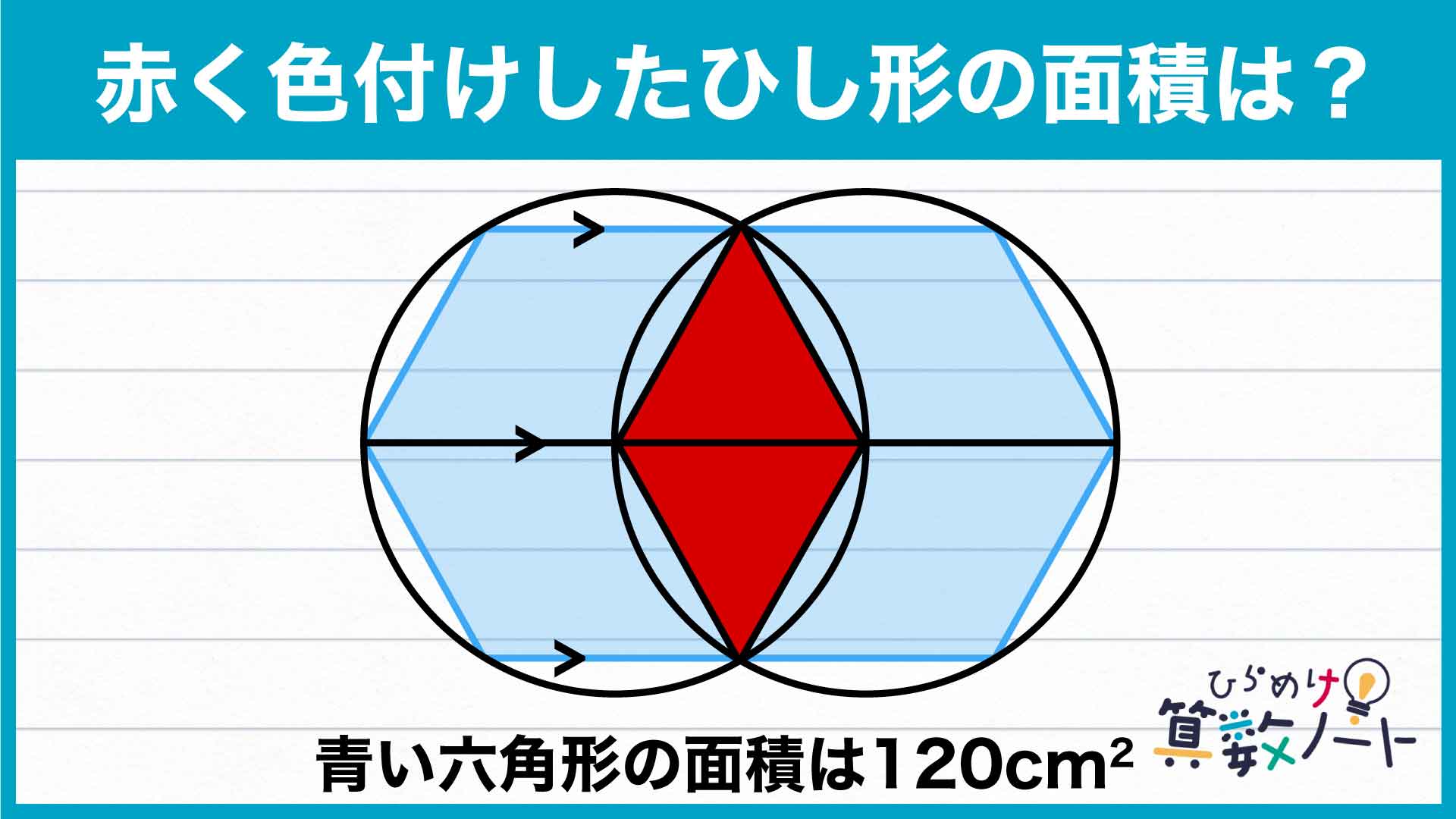
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
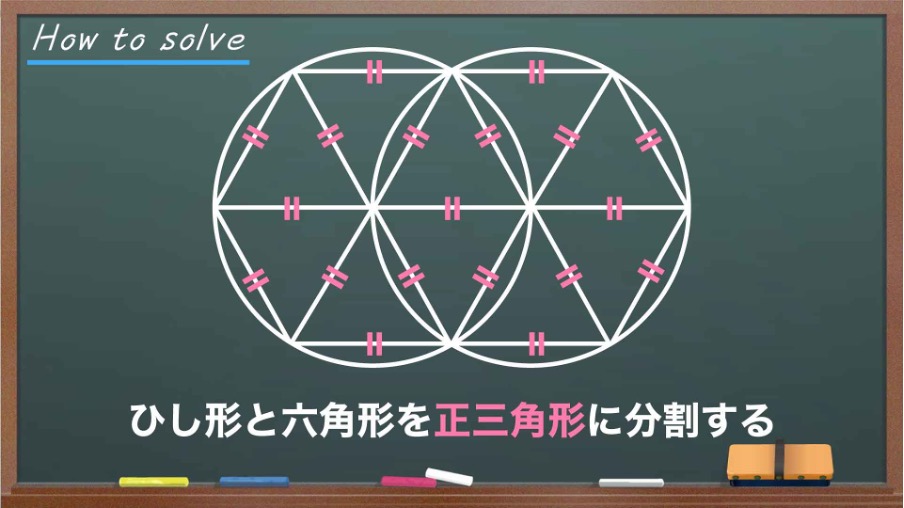
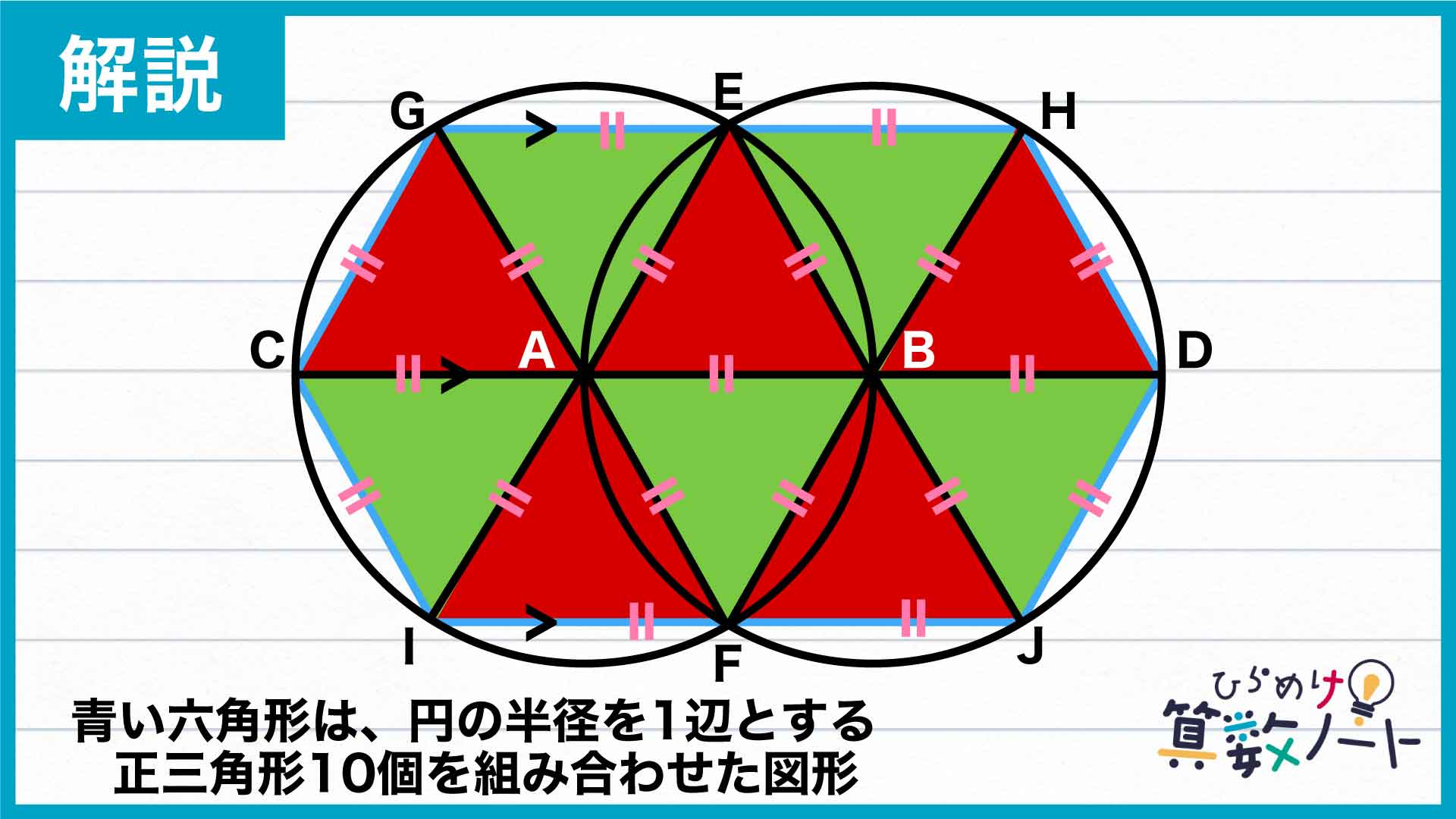
今回の問題の解き方をまとめた図がこちらです。ポイントはひし形と六角形を正三角形に分割することです。
このポイントをもとに、解いていきましょう!
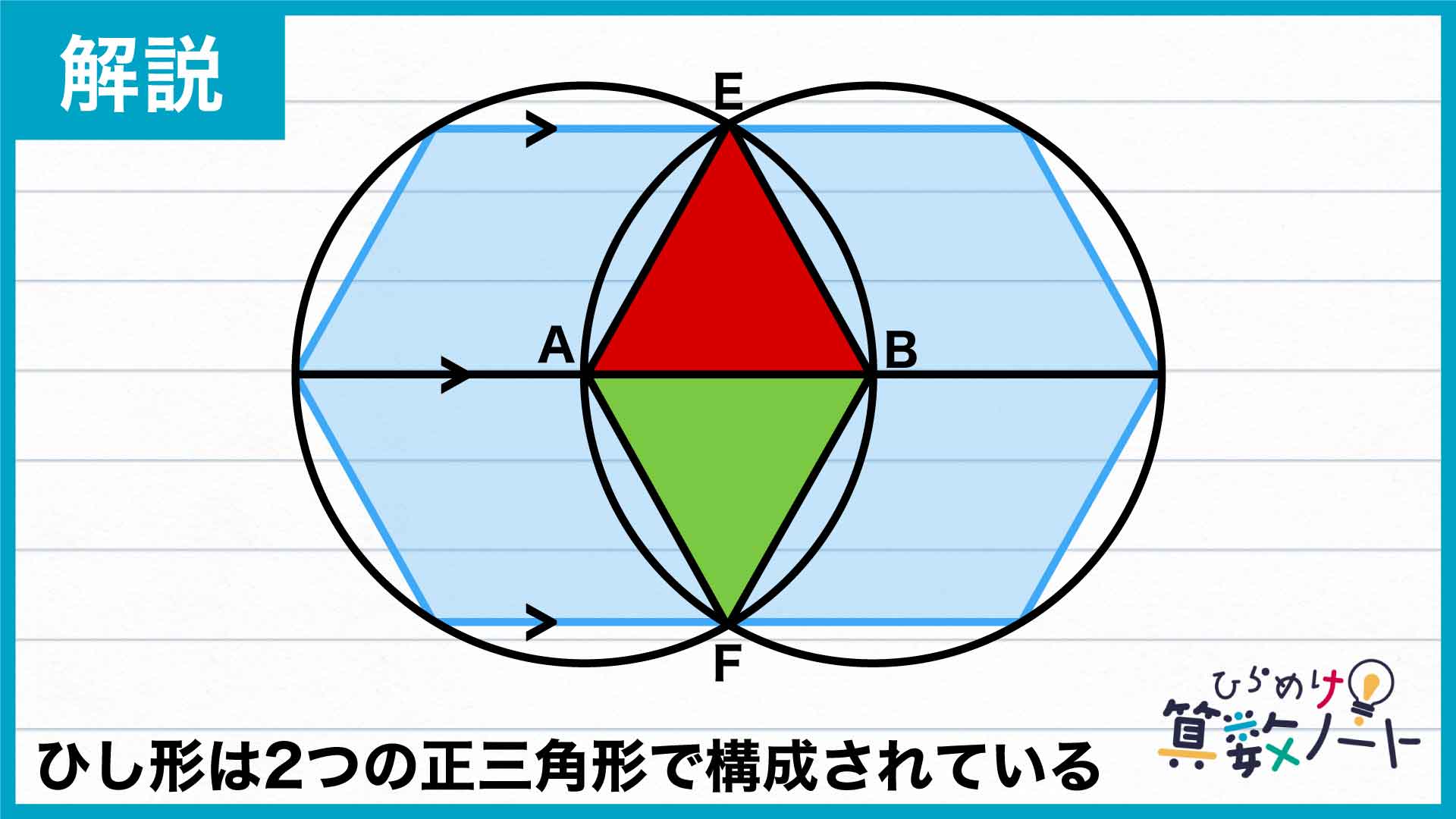
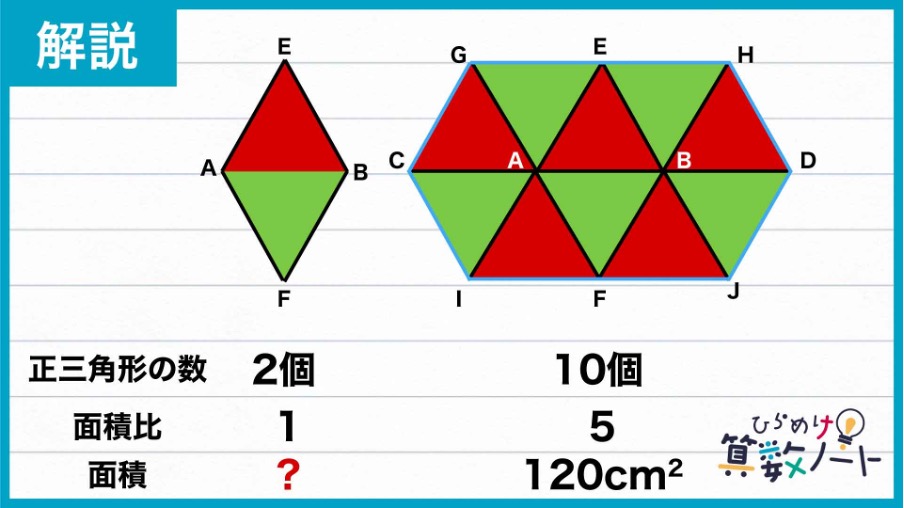
ひし形を2つの三角形に分割する
ひし形EAFBは三角形ABEと三角形ABFを組み合わせた図形です。
三角形ABEも三角形ABFも、すべての辺が円の半径となっているため長さが等しく、ともに正三角形であることがわかります。
六角形を正三角形に分割する
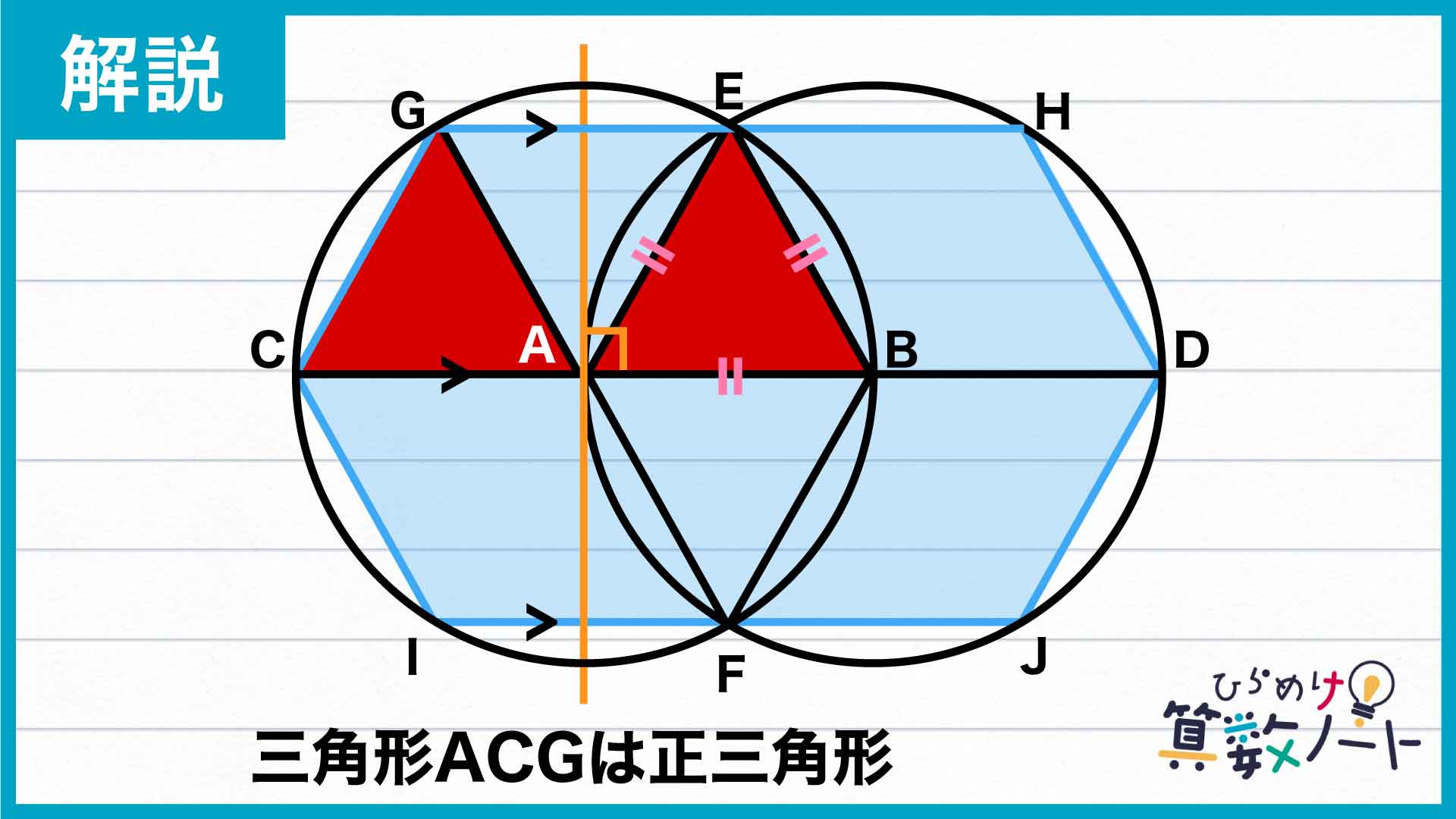
次に、正三角形ABEと合同な図形を六角形GCIJDHの中から探していきましょう。探すにあたって、点Aを通って直線CDに垂直に交わる線を引きます。
すると、円Aはこの垂線に対して線対称であり、直線GHは直線CDと平行であることから、三角形ACGは三角形ABEと合同で正三角形であることがわかります。
また、角BAE=角CAG=60度であることから、角EAG=180-角BAE-角CAG=60度です。このことと、EA=GAであることから、三角形EAGも円の半径を1辺の長さとする正三角形であることがわかります。
同様にして考えると、三角形ACI、FAI、EBH、BDH、FBJ、BDJも円の半径を1辺とする正三角形です。
以上より、六角形GCIJDHは、円の半径を1辺とする正三角形を10個組み合わせた図形であるとわかります。
ひし形EAFBは、同じ正三角形を2つ組み合わせた図形であるため、ひし形EAFBと六角形GCIJDHの面積比は2:10=1:5です。
したがって、ひし形EAFBの面積は120÷5=24cm2と求められます。
答え:24cm2
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】














.jpg)







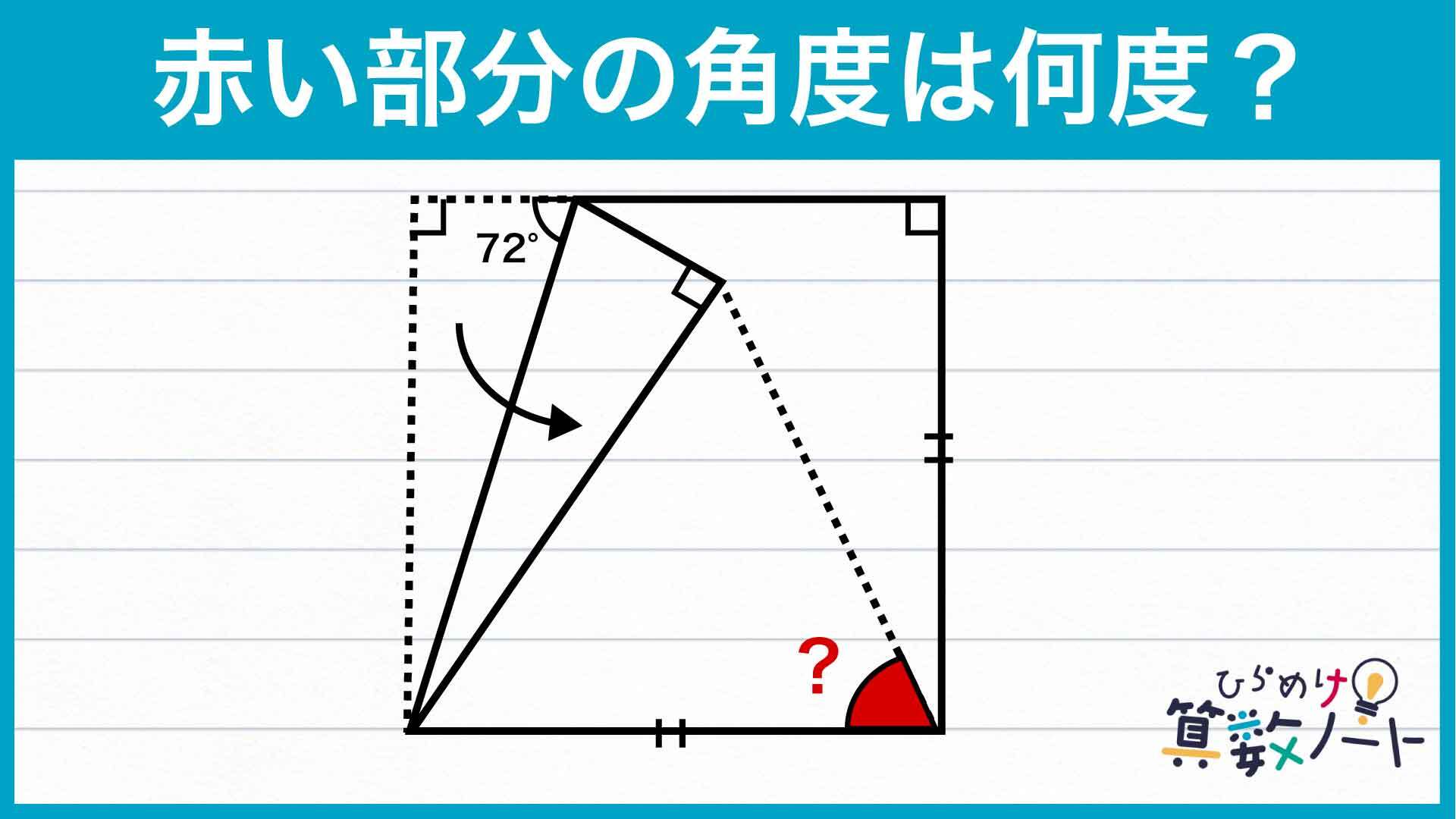

.jpg)






