解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
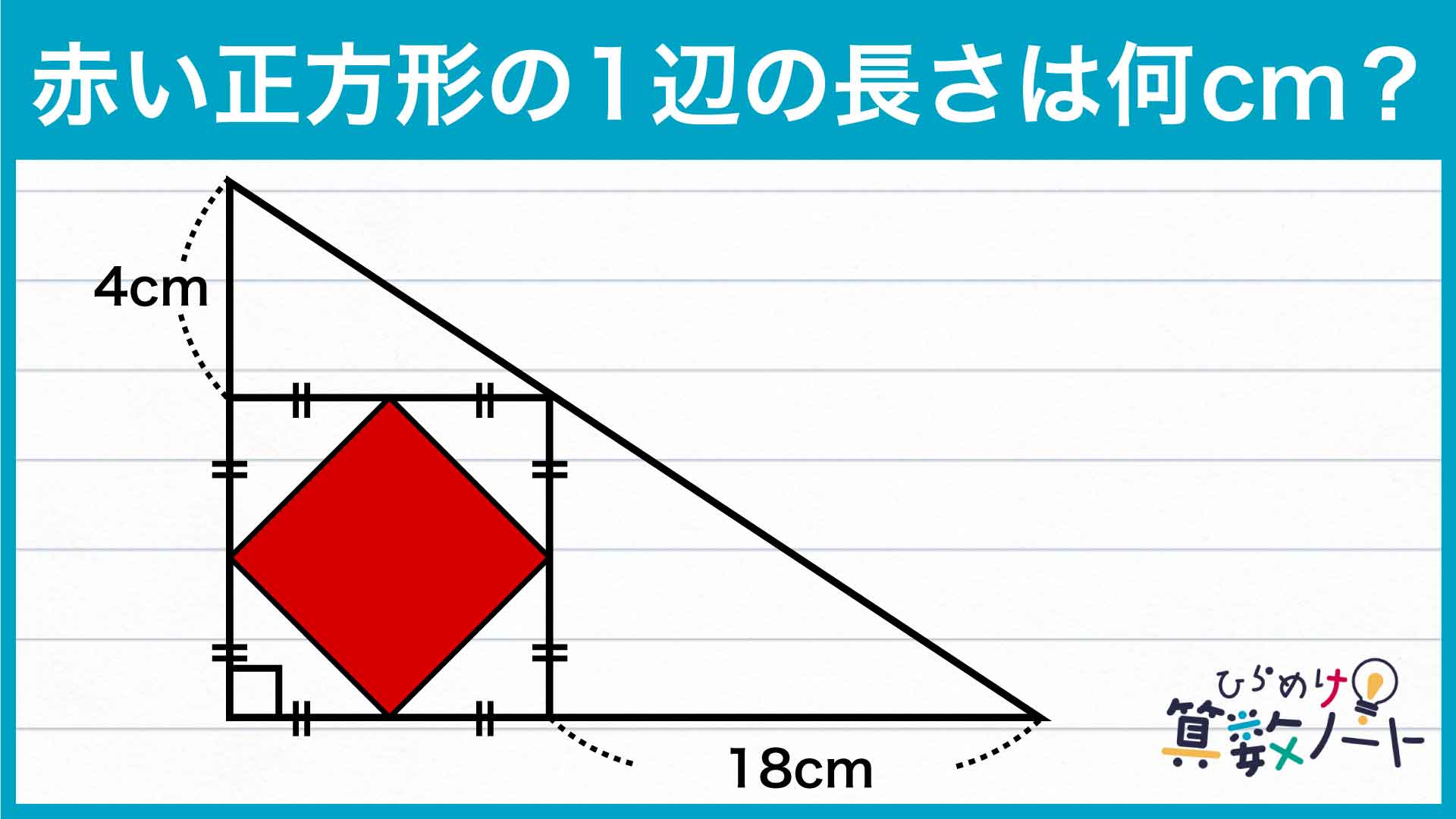
今回は私と一緒に解いていきましょう! 赤い正方形の一辺の長さを求めるために、大きな正方形の面積を求めたいところですが……?
今回の重要なポイントはこちらです。
2つの三角形が相似の関係にあるとき、対応する辺の長さの比は等しくなります。この性質を利用すれば、大きな正方形の面積を求めることができ、答えに大きく近づくことができます。
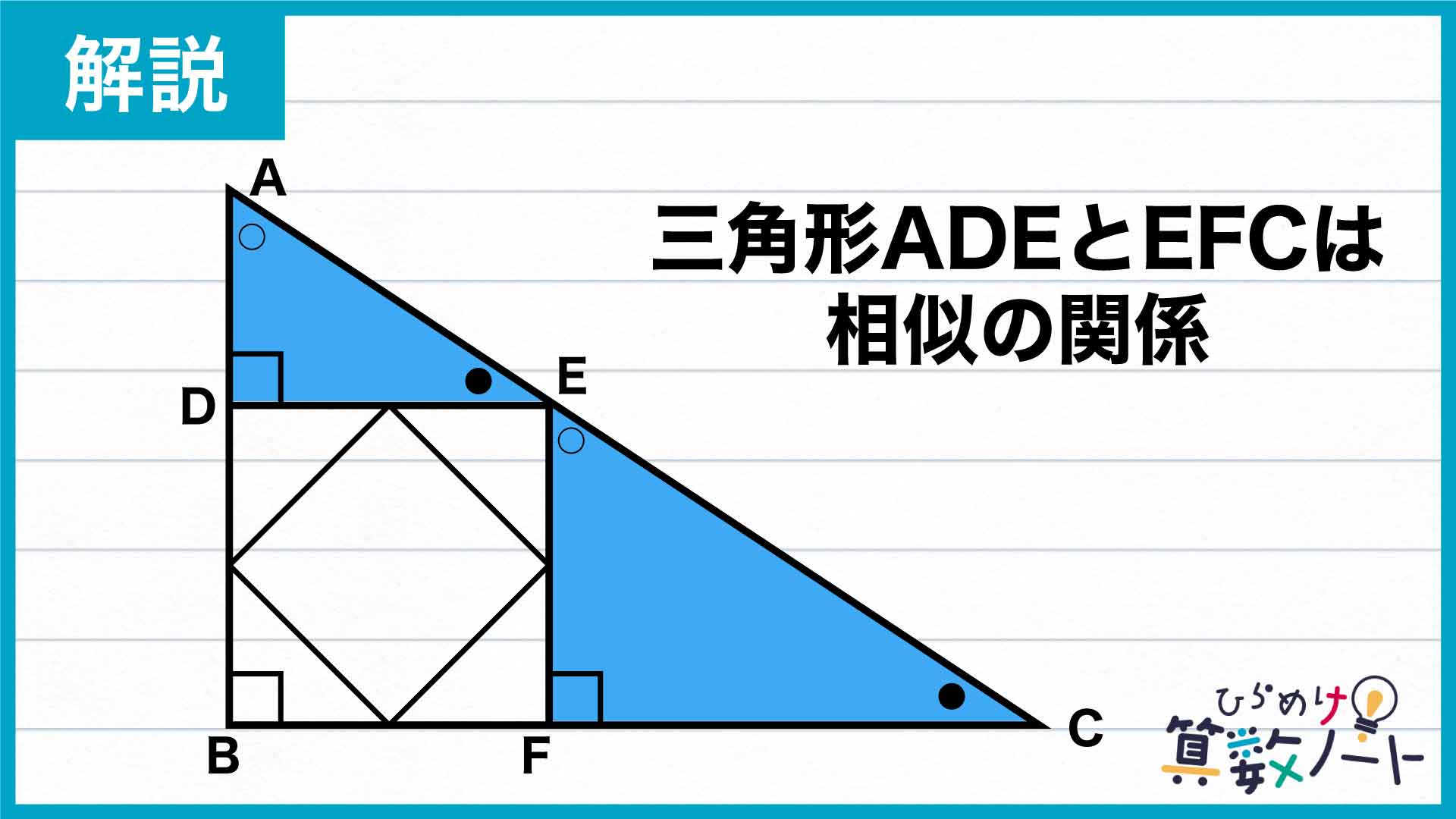
三角形ADEとEFCの関係を調べる
まずは、三角形ADEとEFCの関係を調べます。手始めに、角BACと角ACBを次のように置きます。
すると、
- 角BACと角ACBの和が90度であること
- 角ADE、角EFCがそれぞれ90度であること
よって、三角形ADEとEFCは、対応する3つの角の大きさがそれぞれ等しいので相似の関係だとわかりました。
相似の関係から三角形ADEとEFCの辺に関する比の関係を見いだす
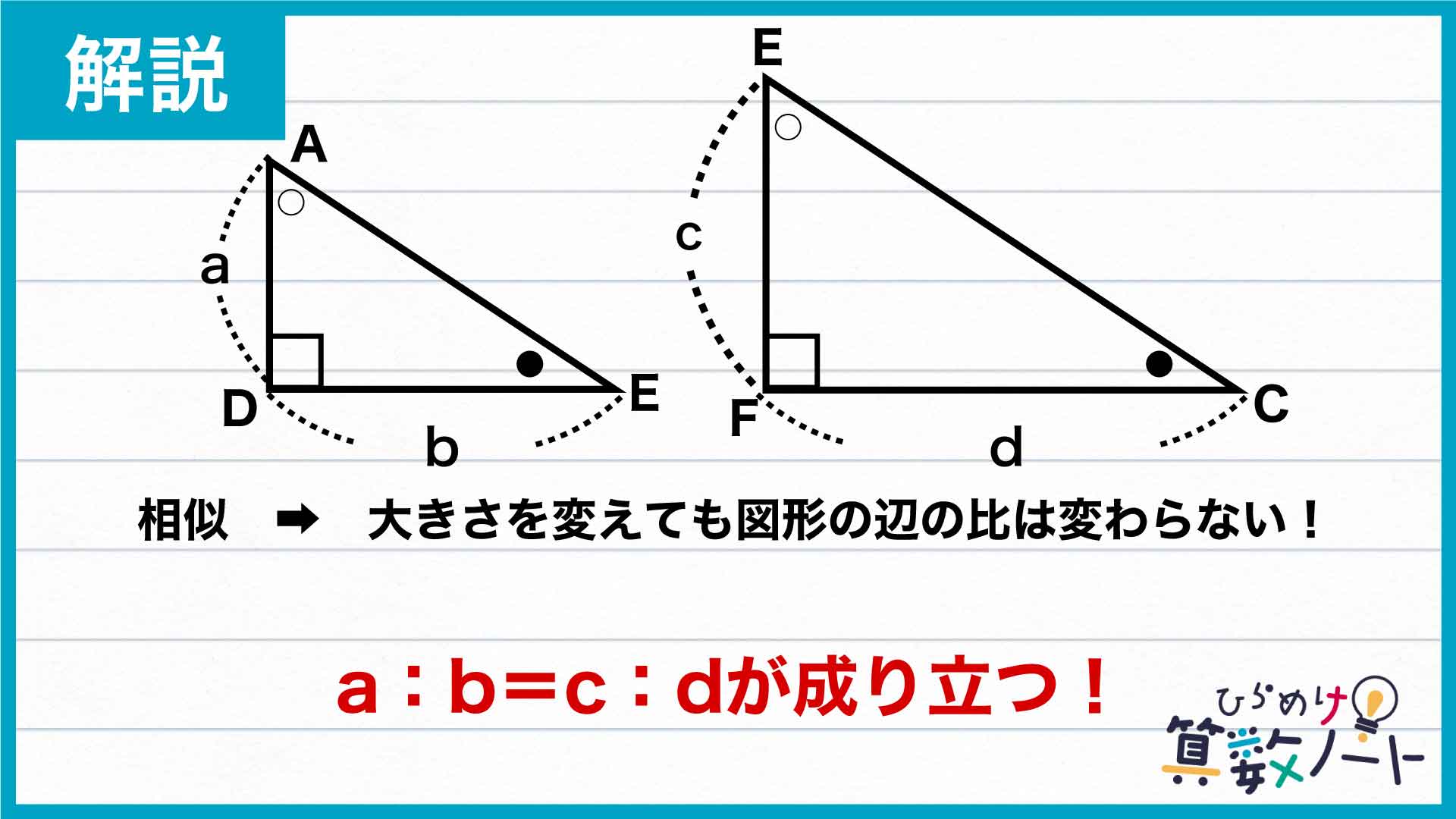
先ほど、三角形ADEとEFCが相似の関係にあることがわかりました。
相似な図形において対応する辺の長さの比は同じのため、辺ADと辺DEの比と、辺EFと辺FCの比は同じです。
この性質から、AD:DE=EF:FCが成り立ちます。
比の性質から辺DEと辺EFの積を求める
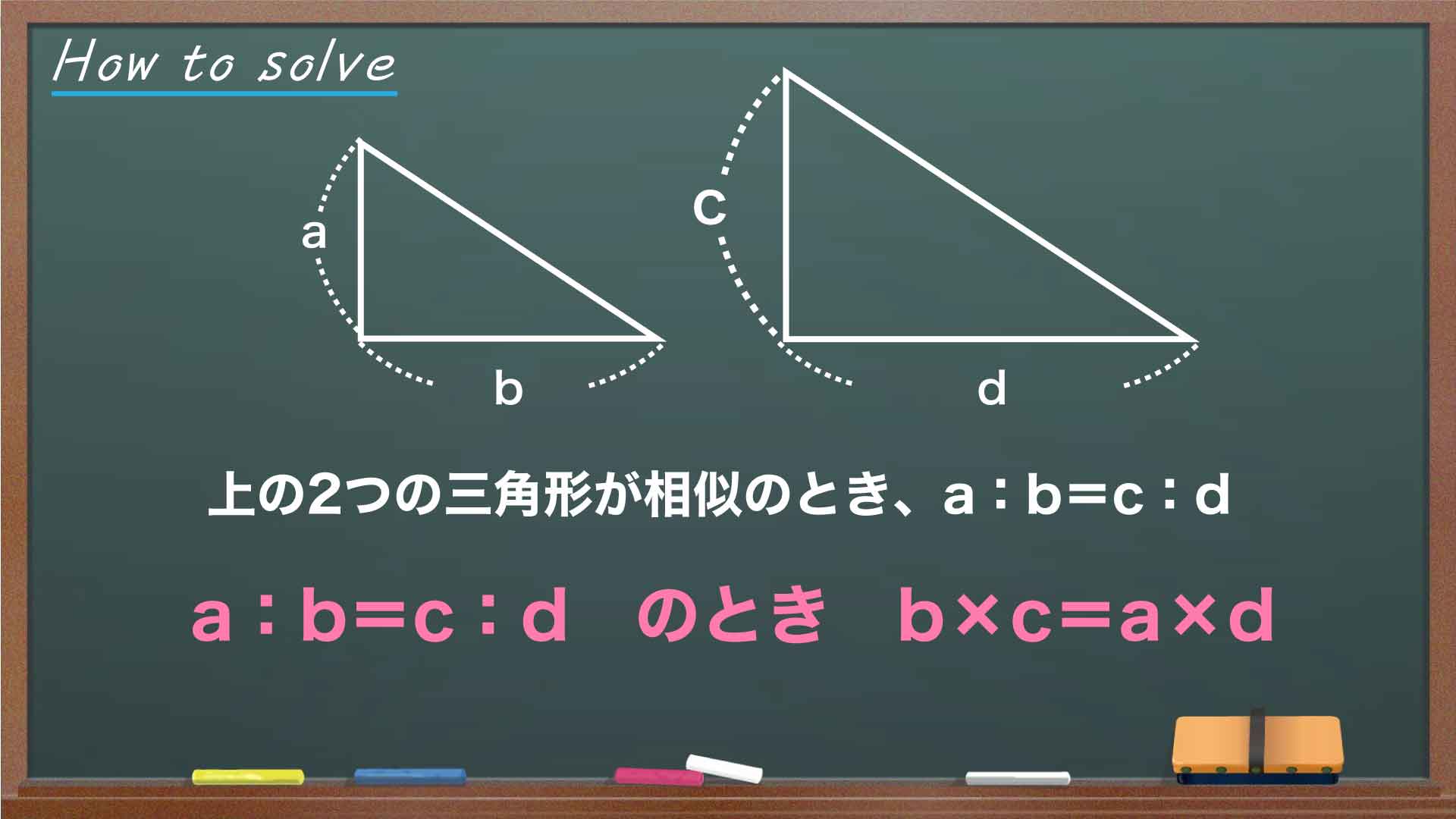
ここで、比の性質に関する重要なポイントを見てみましょう。
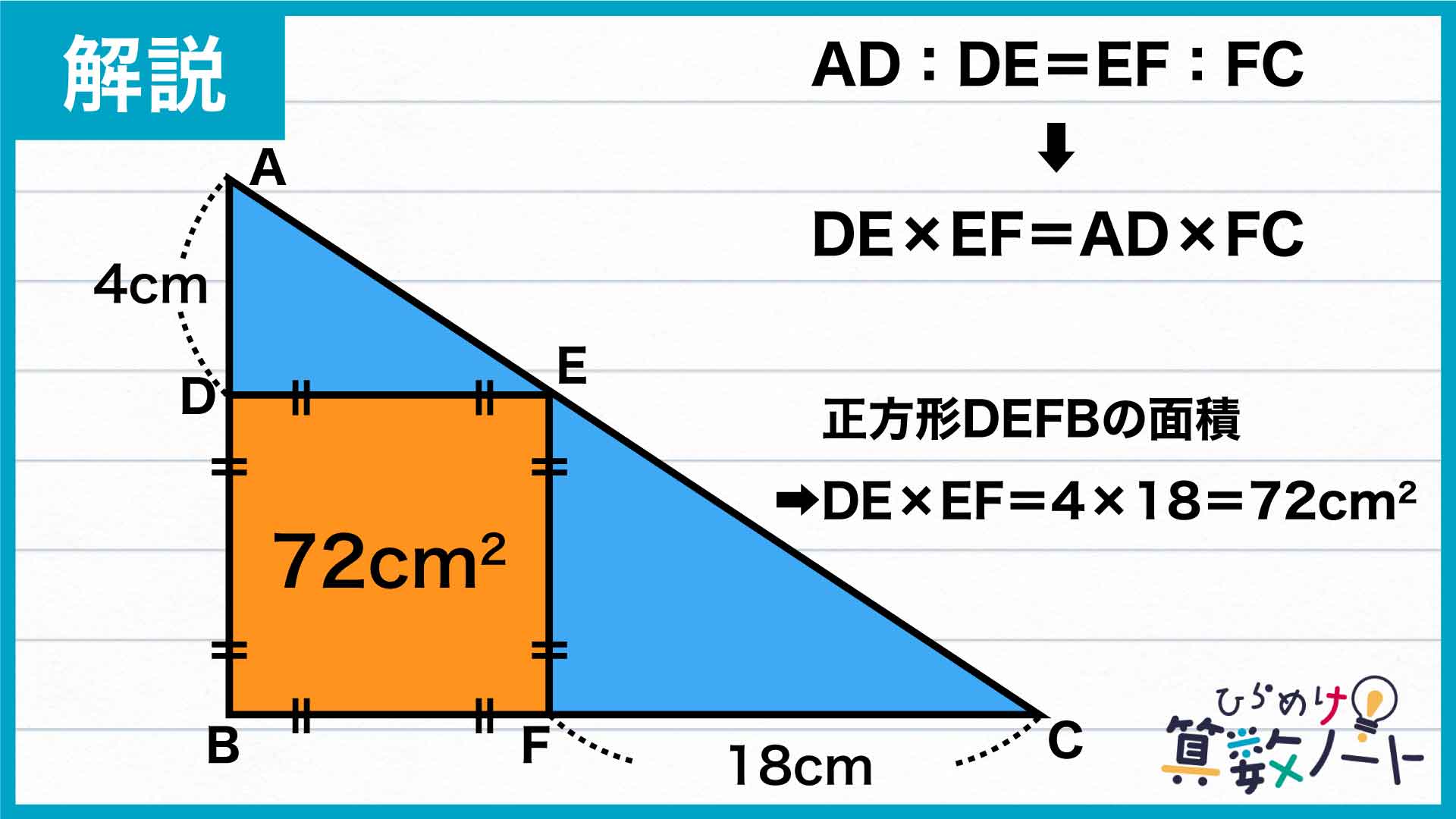
このポイントを用いて、先ほど算出したAD:DE=EF:FCという式を変形すると、DE×EF=AD×FCとなります。
辺AD、辺FCの長さはそれぞれ4cm、18cmとわかっていますので、辺DEと辺EFの積は4×18=72となります。したがって、正方形DEFBの大きさは72cm2と求めることができます。
大小2つの正方形の関係から辺GHの長さを求める
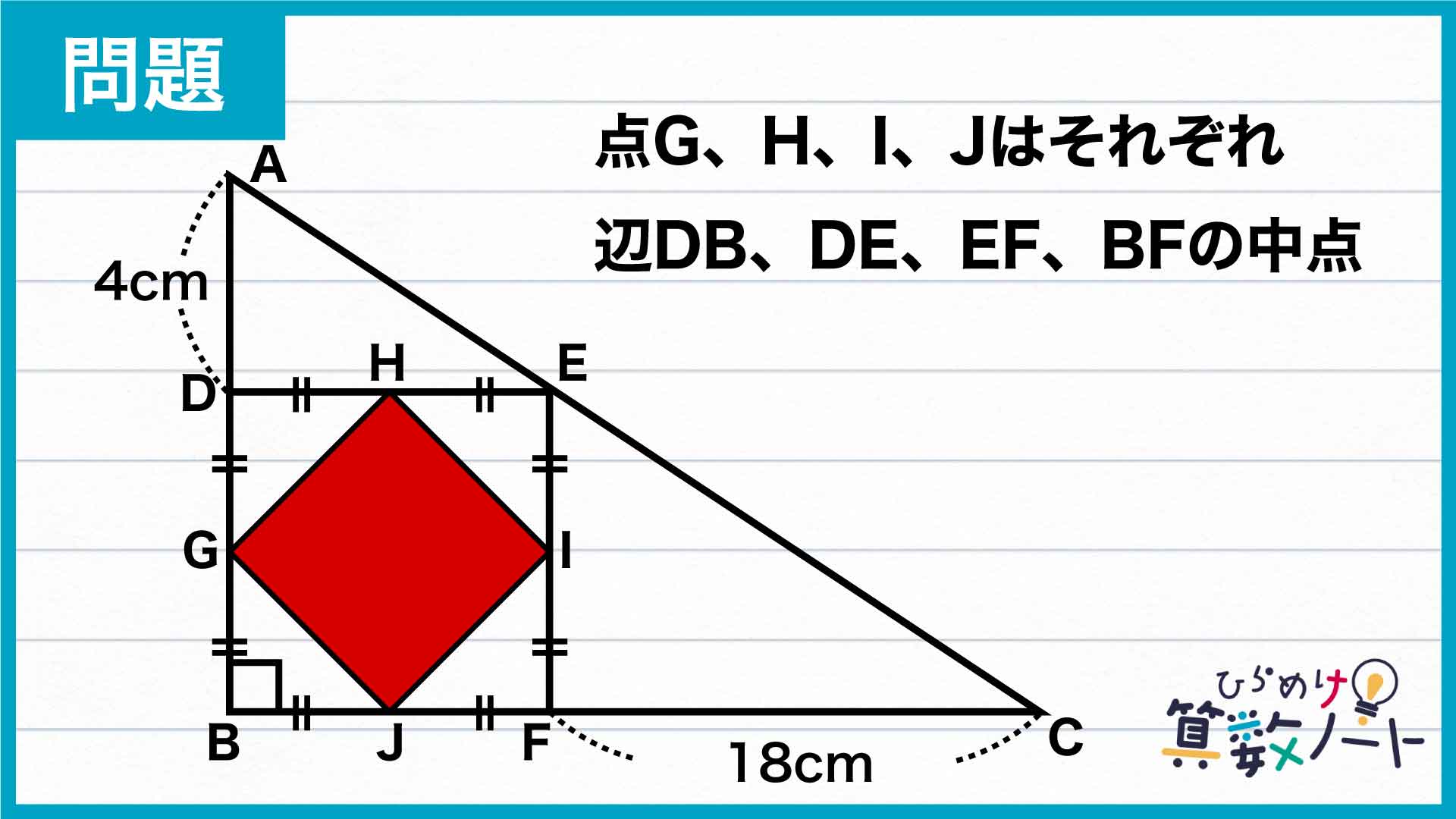
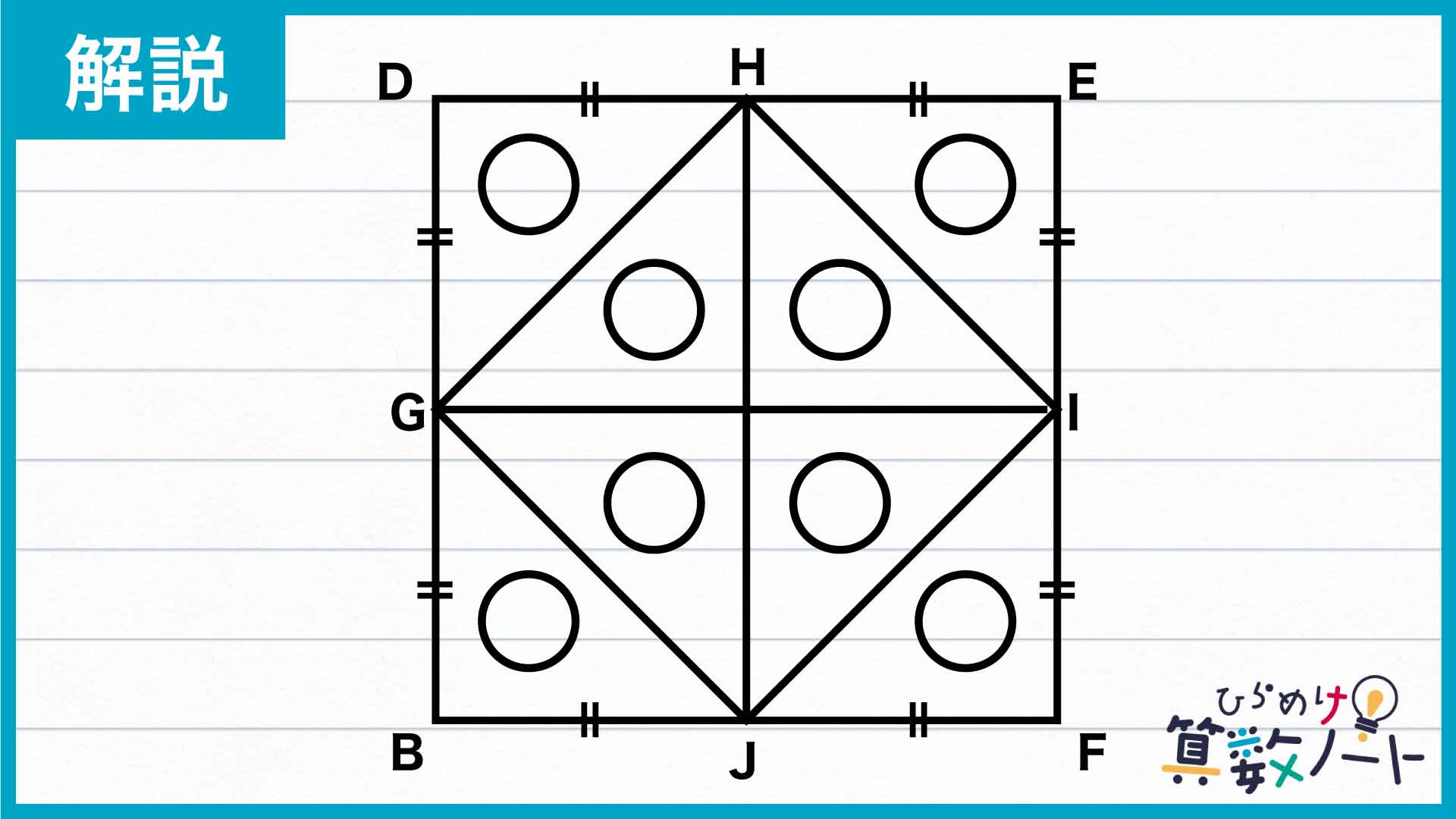
小さい正方形の頂点は、大きい正方形の各辺の中点です。大きい正方形を次のように分解します。
上の図で、丸印が付いた三角形は、点G、H、I、Jが正方形DEFBの中点であることからすべて同じ大きさとなります。大きい正方形は8個、小さい正方形は4個の丸印がついた三角形で構成されているので、小さい正方形は大きい正方形の2分の1の大きさであることがわかります。
したがって、小さい正方形の面積は72÷2=36cm2なので、小さい正方形の1辺の長さは、(1辺の長さ)×(1辺の長さ)=36cm2、すなわち6cmと求めることができます。
答え:6cm
相似の関係と比の性質、この2つをうまく使えるかがポイントでした。
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】











.jpg)









.jpg)