解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
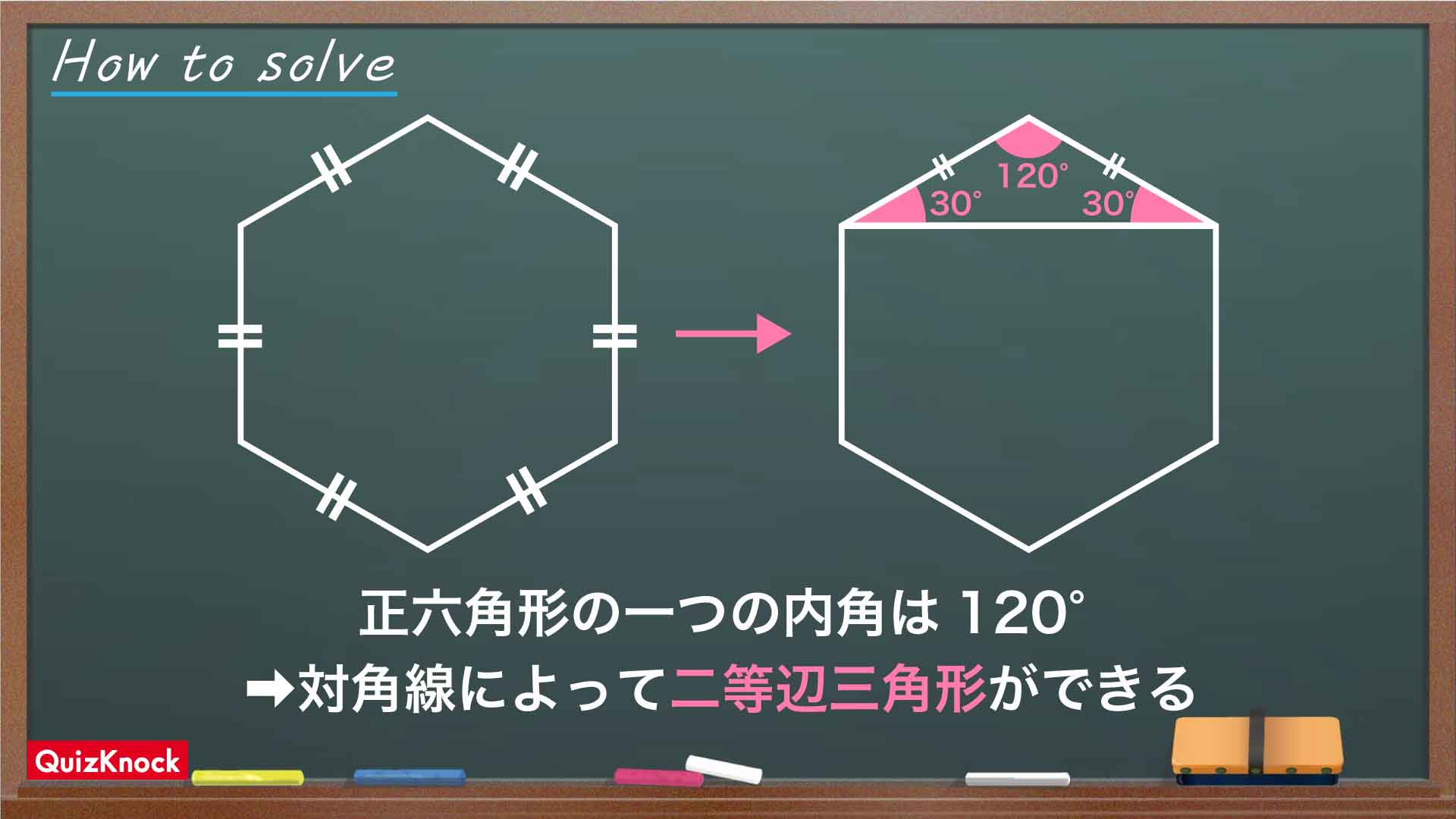
今回のポイントは、「正六角形に引かれた対角線」です。
正六角形の1つの角の大きさは120度なので、以下のように対角線を引くと頂角が120度の二等辺三角形があらわれます。
以上を踏まえ、問題を解いていきましょう!
補助線を引く
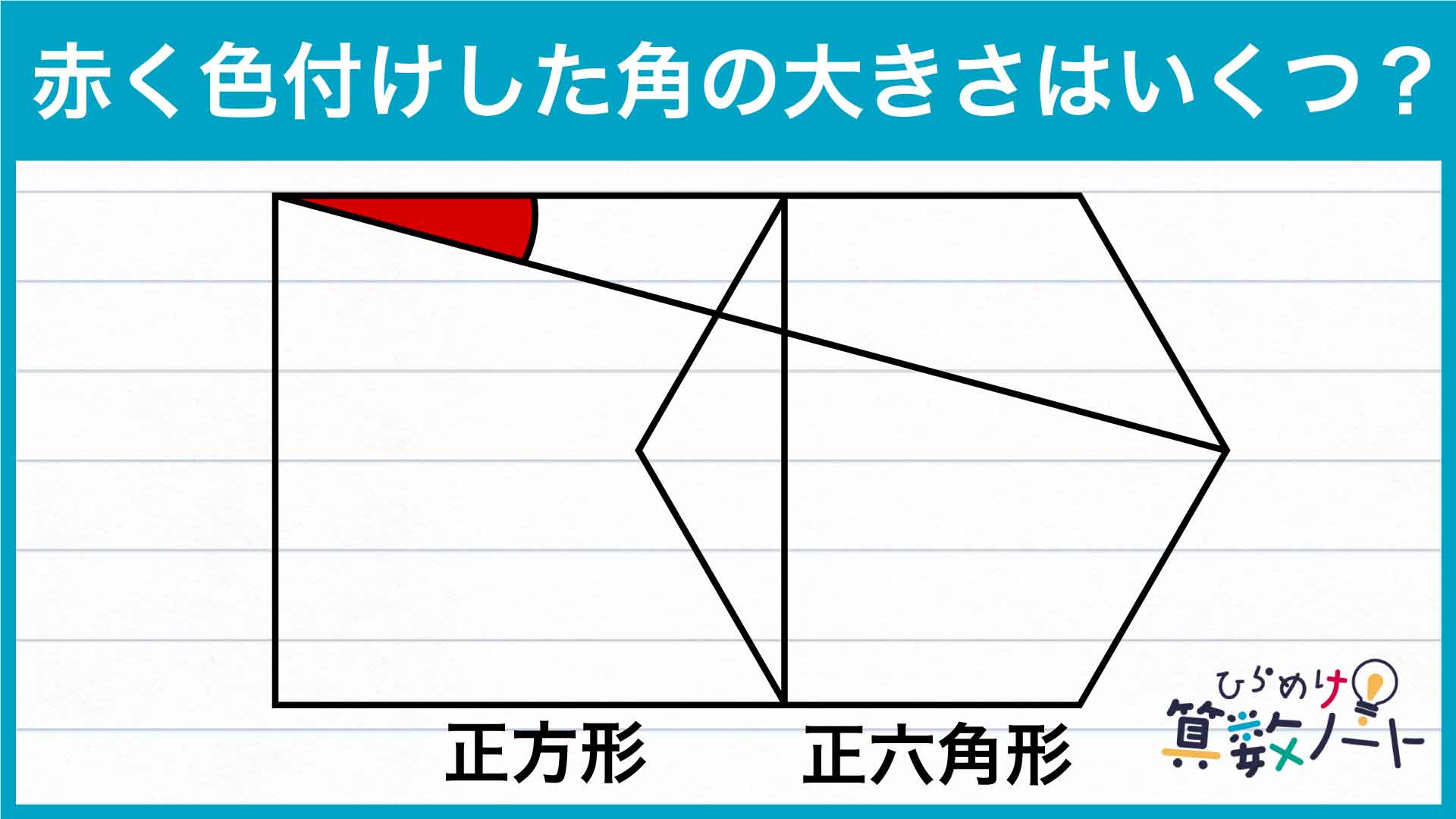
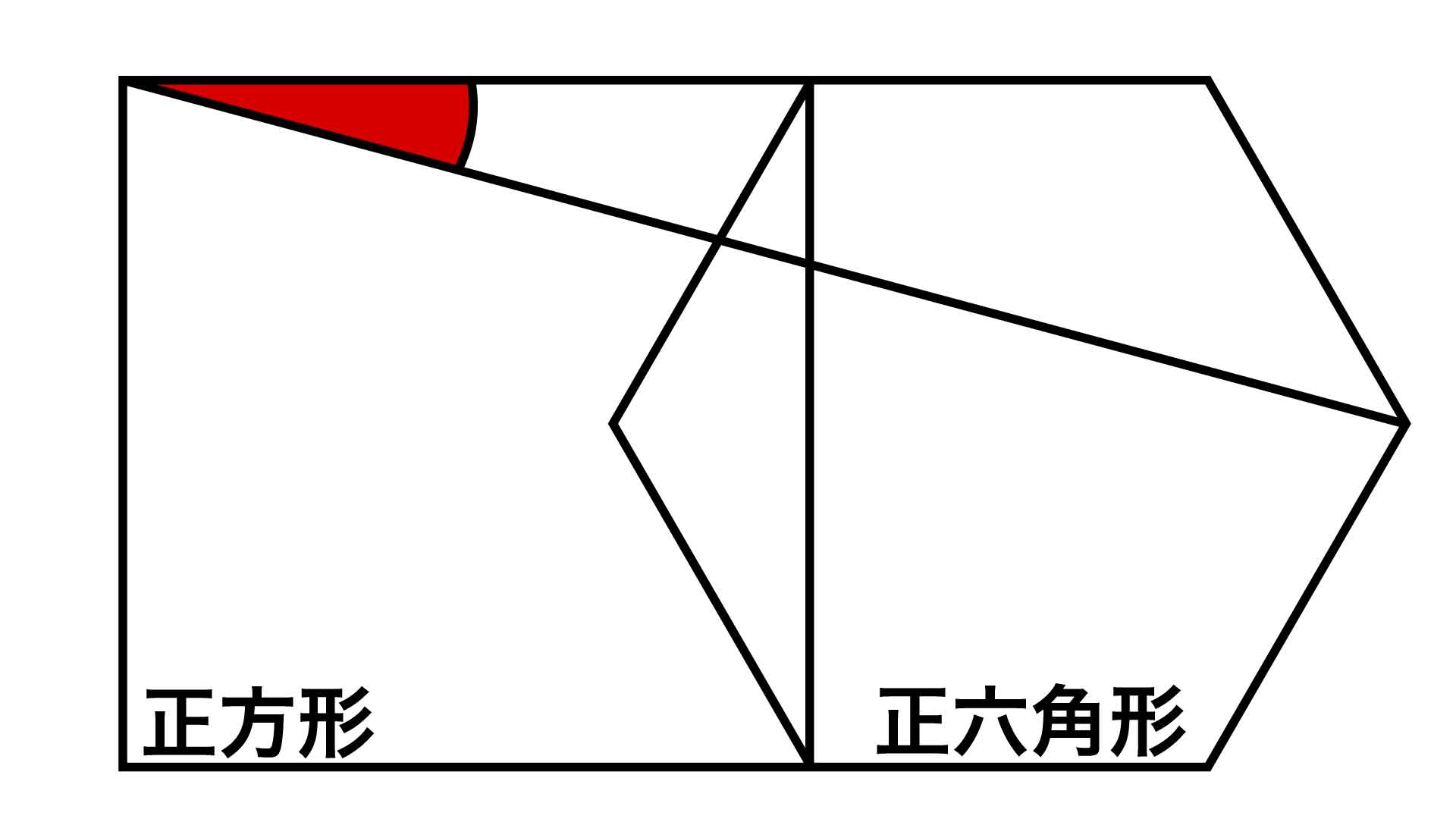
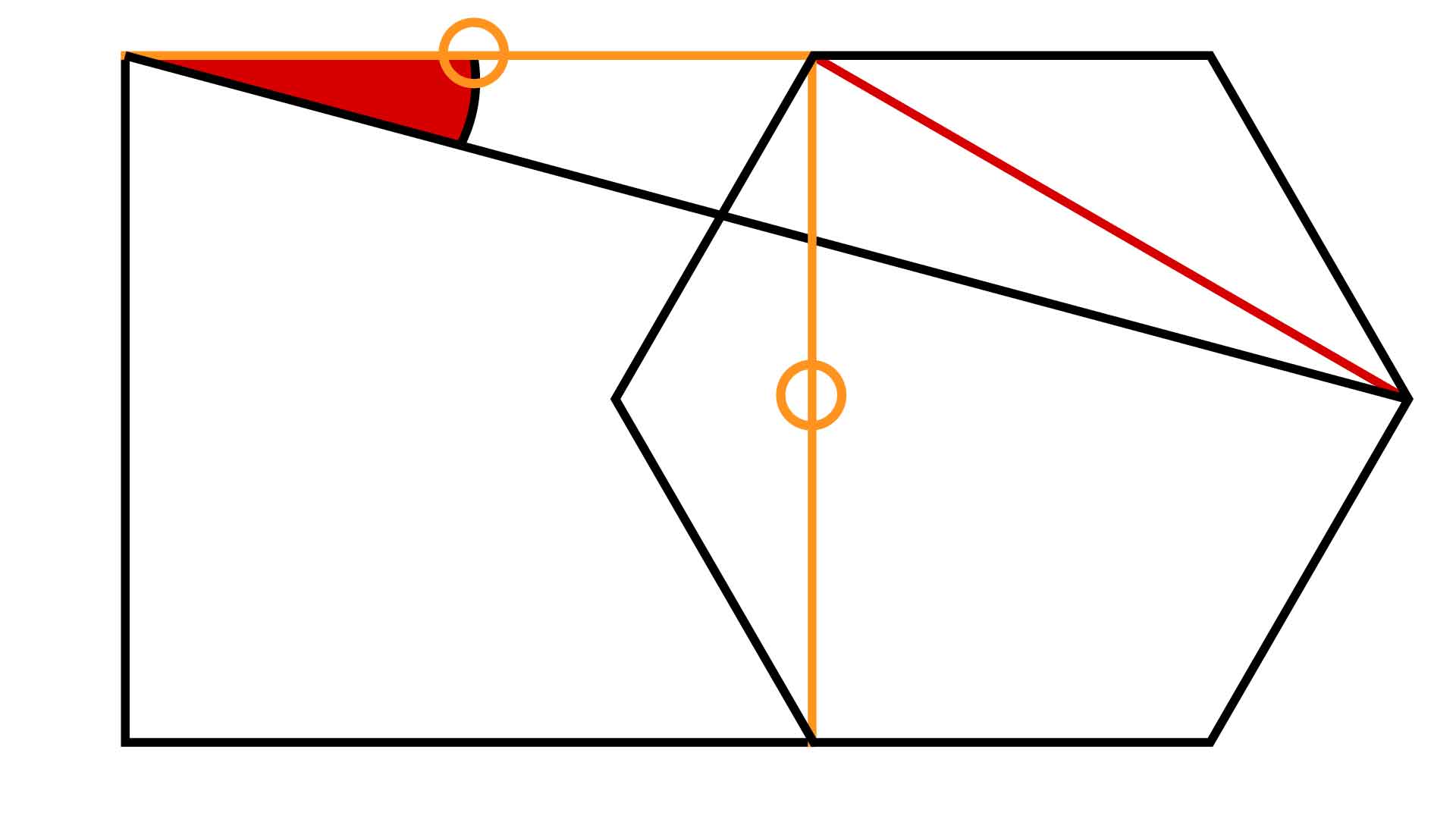
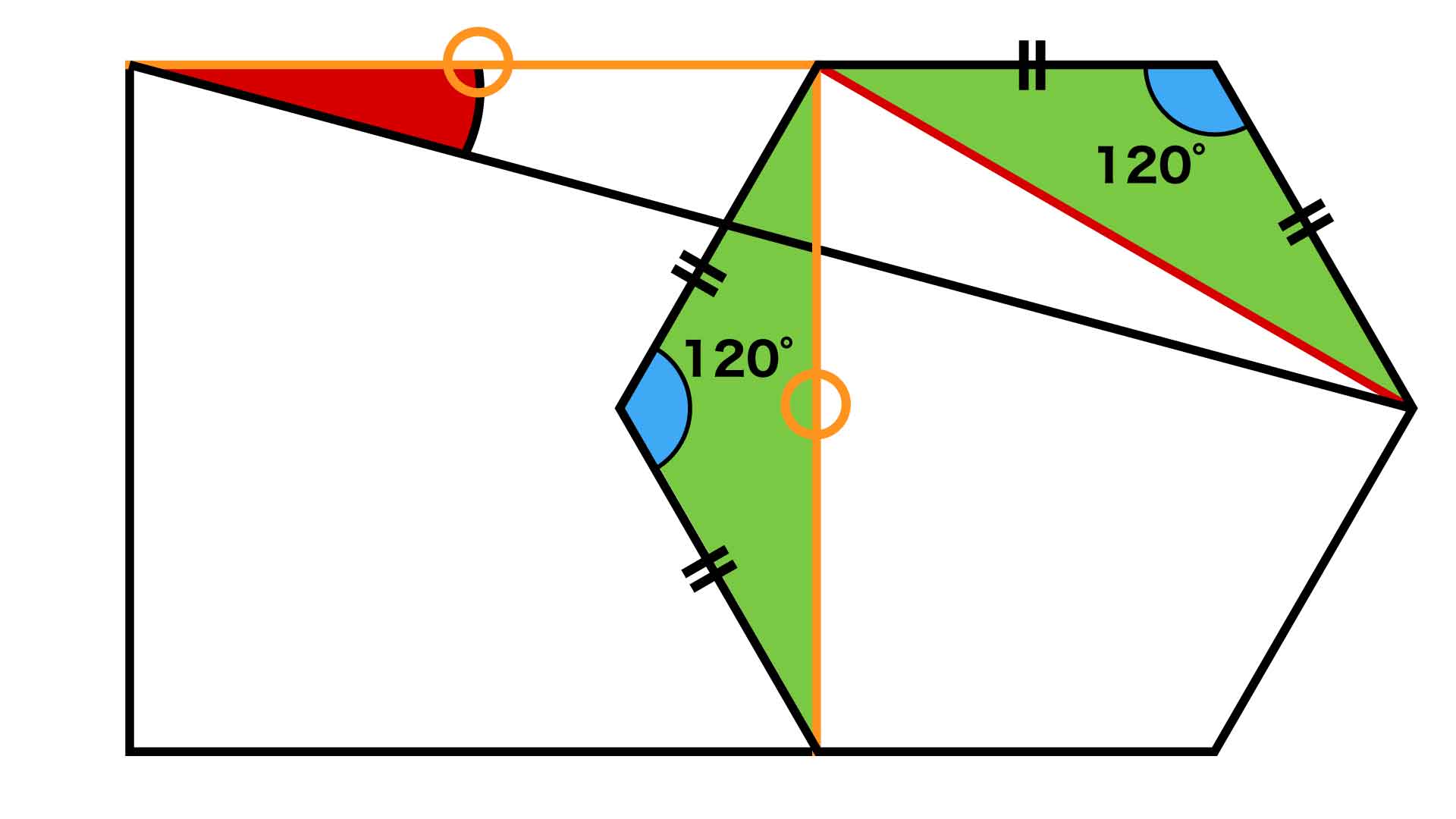
問題の図において与えられている最大の情報は、正方形の1辺と正六角形の対角線の長さが等しいことです。これを最大限に活用するため、下の図で赤く示した補助線を引きます。
引いた補助線は、正六角形の対角線になっています。つまり、下の図で緑色に示した2つの三角形は、等しい2辺と間にはさまれた120度の角をいずれももつため、合同の関係にある二等辺三角形だとわかります。
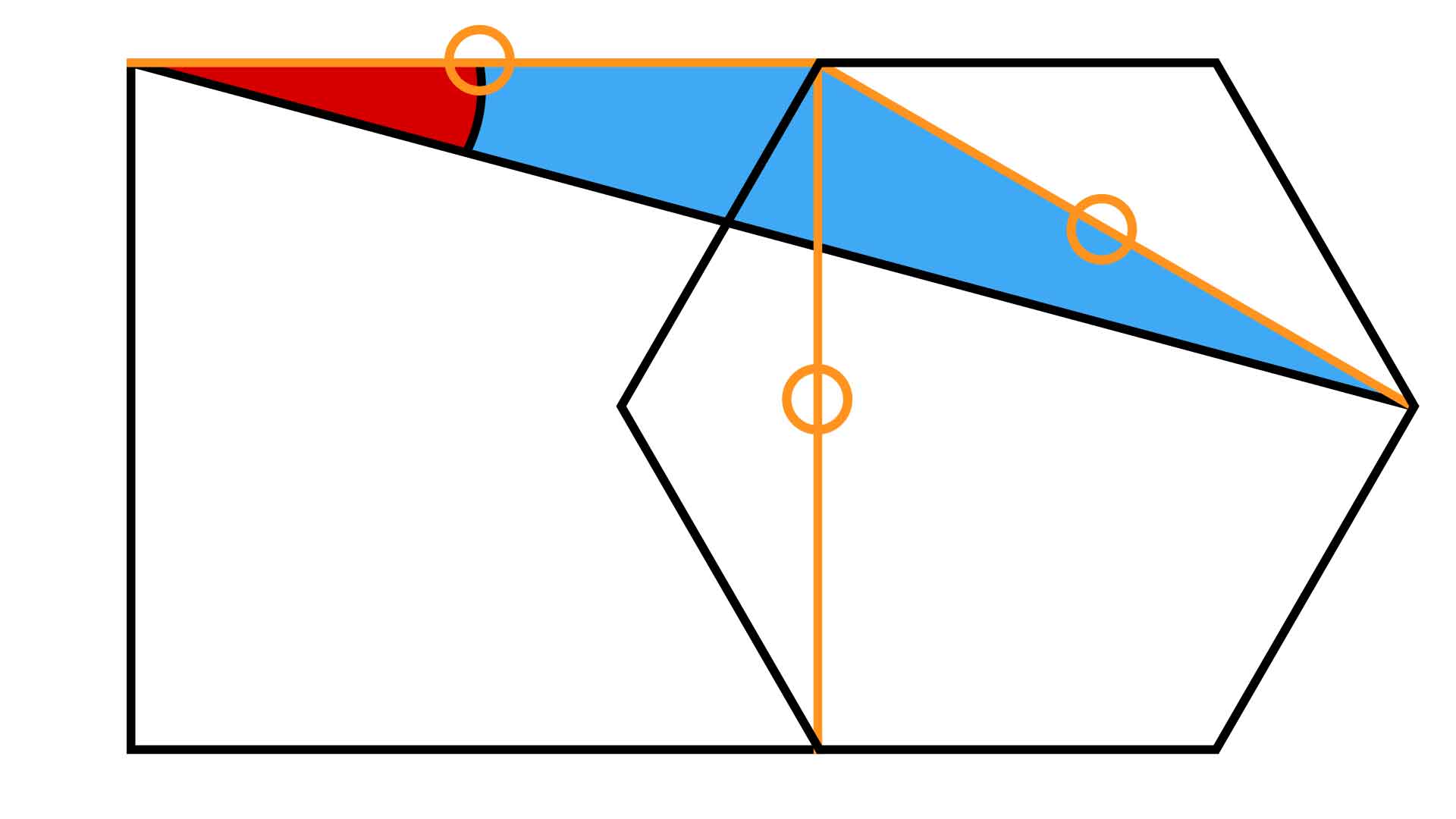
よって、補助線の長さは正方形の1辺の長さと等しくなり、下の図で青く示した三角形は二等辺三角形だとわかります。
角の大きさを求める
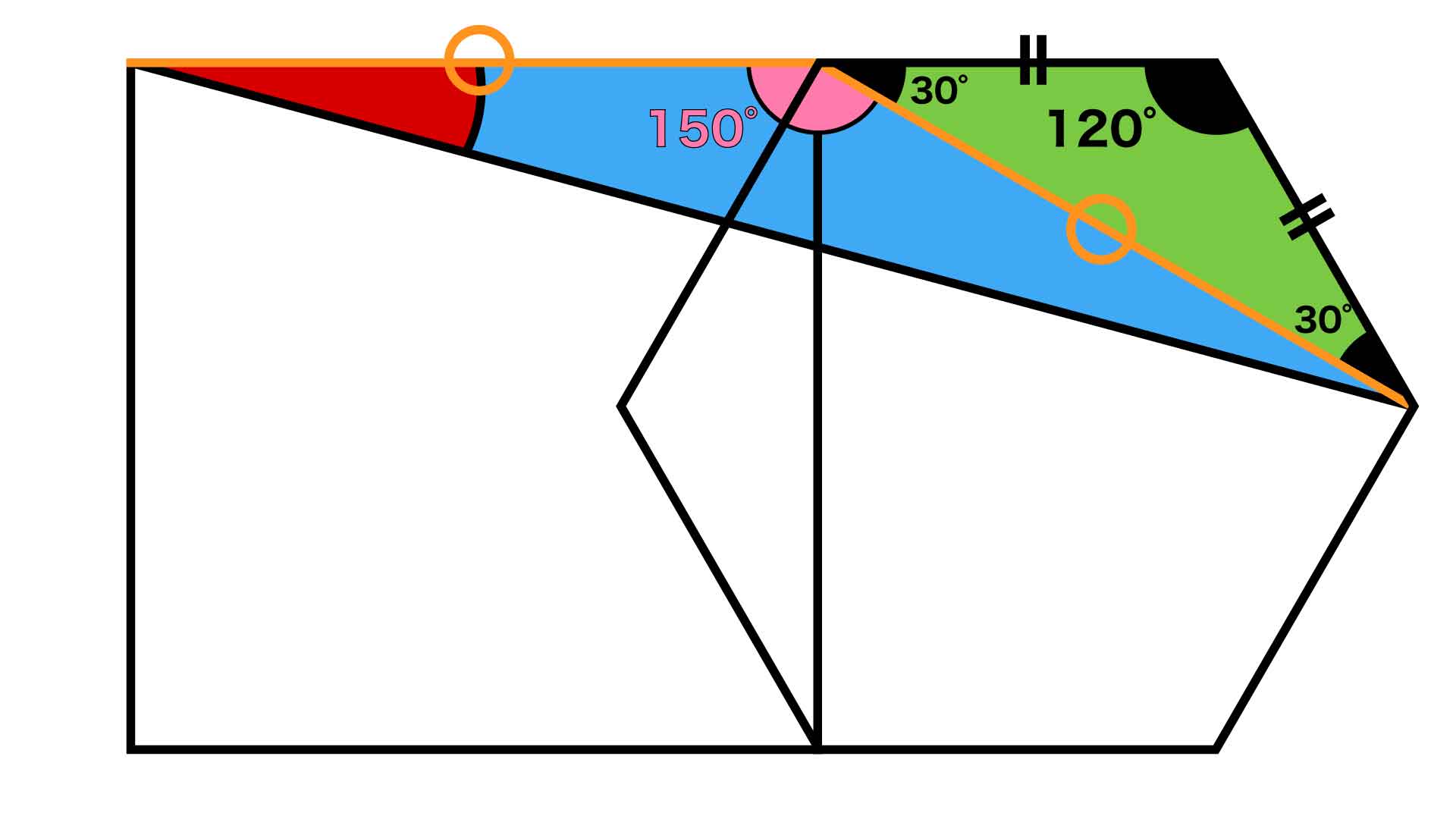
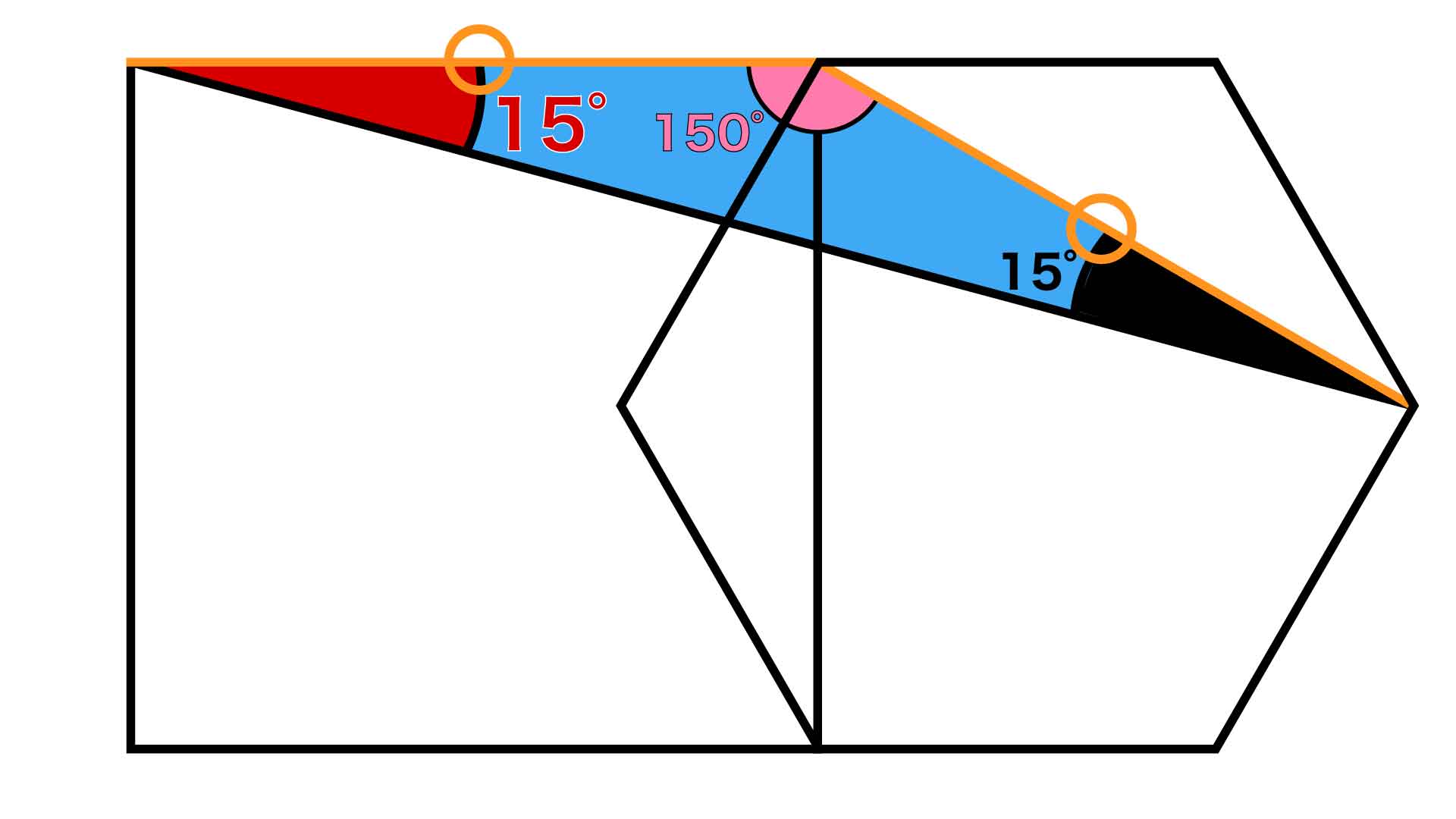
正六角形に対角線を引くと頂角が120度の二等辺三角形ができます。よって、青く示した二等辺三角形の頂角の大きさは、下の図より180-30=150度となります。
以上より、求める角の大きさは、(180-150)÷2=15度となります。
答え:15度
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)








.jpg)







