小学6年生で解ける「長方形の面積」の問題。あなたは解けますか？

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

前ページ：【解答フォーム】自力で解きたい方はこちらへ！　以下は問題の答えです

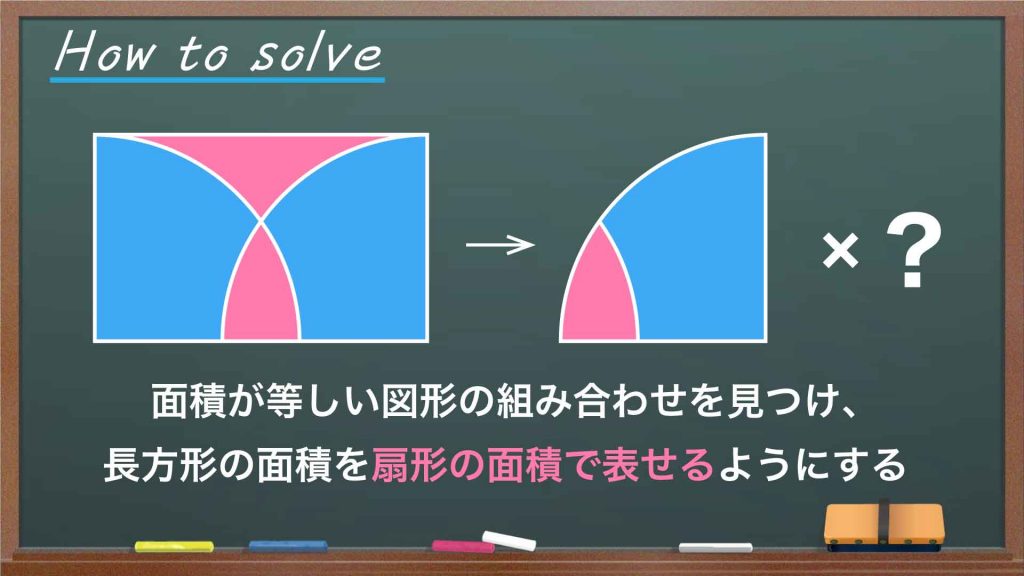
今回の解き方をまとめた図がこちらです。

ポイントは、「面積が等しい図形」を見極め、活用することです。

この流れに沿って問題を攻略していきましょう！

面積が等しい図形はどれ？

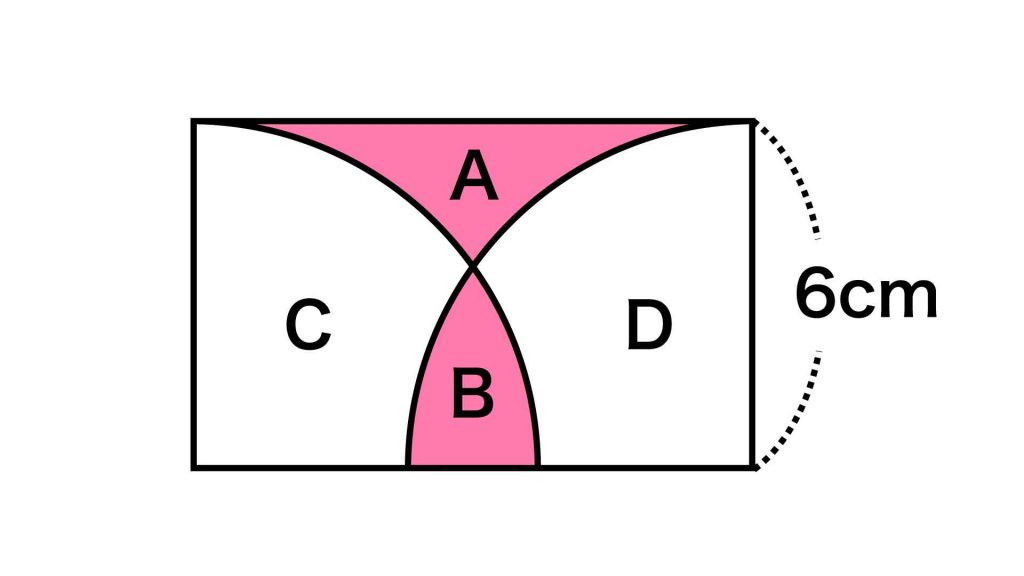
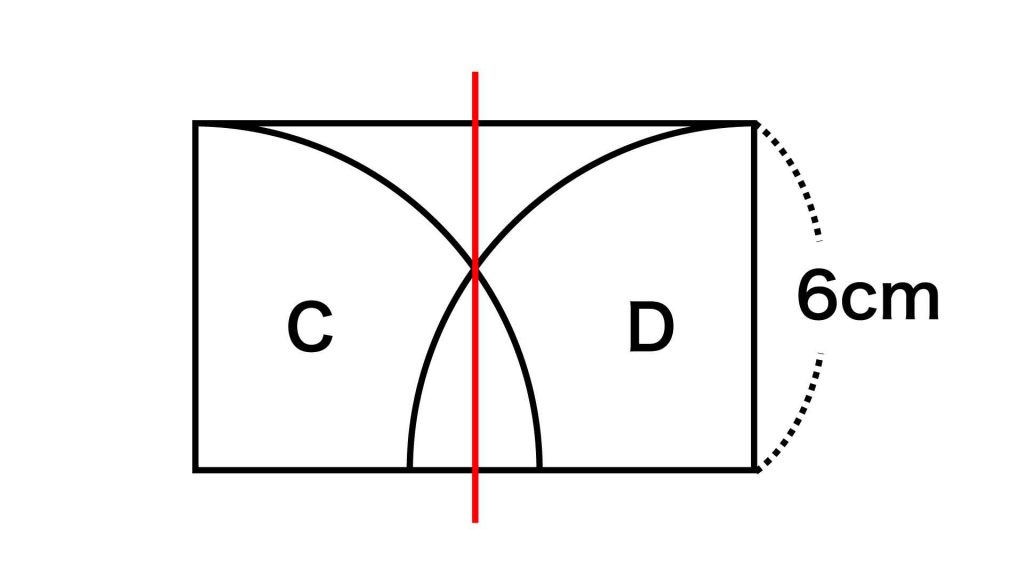
下の図のように、A、Bでない部分の図形をそれぞれC、Dとします。

CとDの関係を知るために、下の図のように扇形の交点を通り長辺に対して垂直な線（赤線）を引きます。CとDは赤線を軸として左右対称であるため、面積は等しいです。

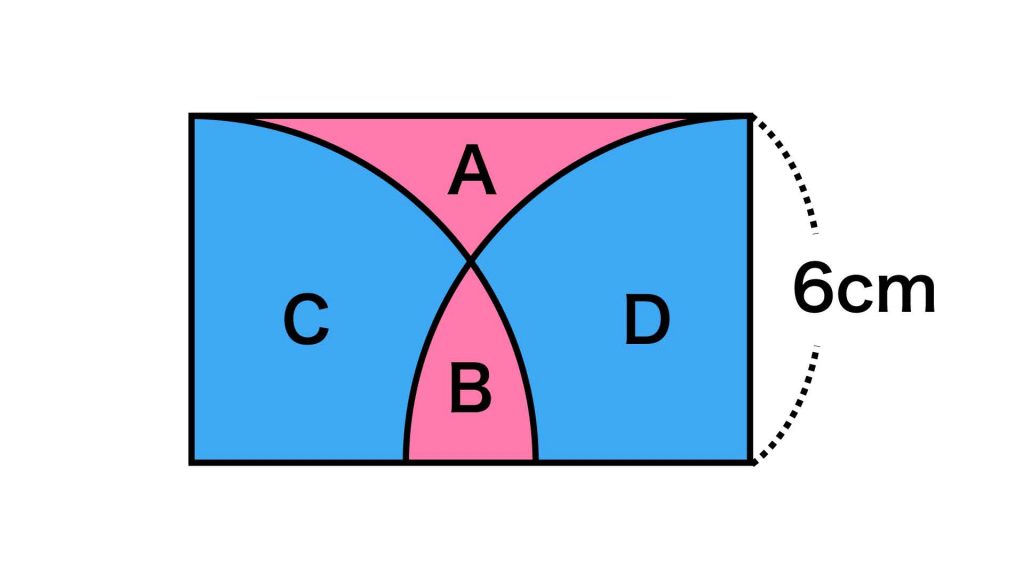
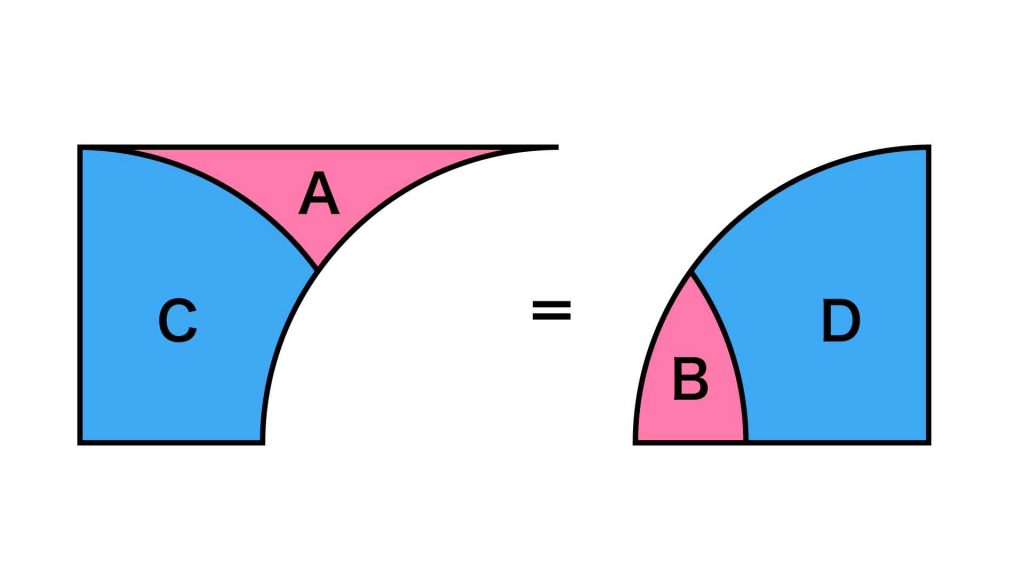
以上より、面積が等しい図形を同じ色で示すと、下の図のようになります。

AとB、CとDのの面積がそれぞれ等しいため、長方形の中にある図形の面積の関係は、A+C=B+Dと表すことができます。

よって、A+CもしくはB+Dの図形の面積を求めることができれば、求めた面積を2倍することで、長方形の面積を求めることができます。

扇形であるB+Dの面積を求める

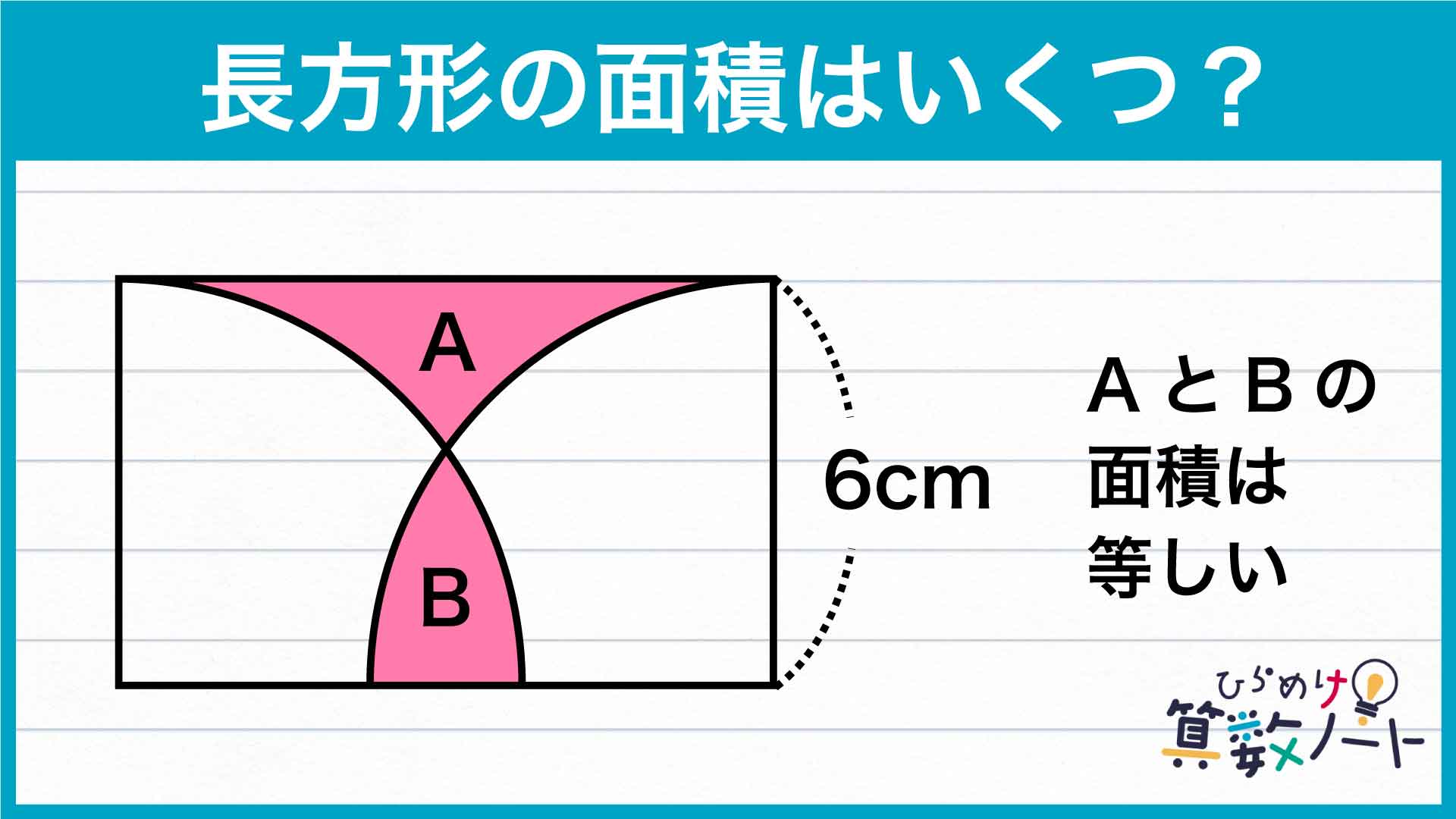
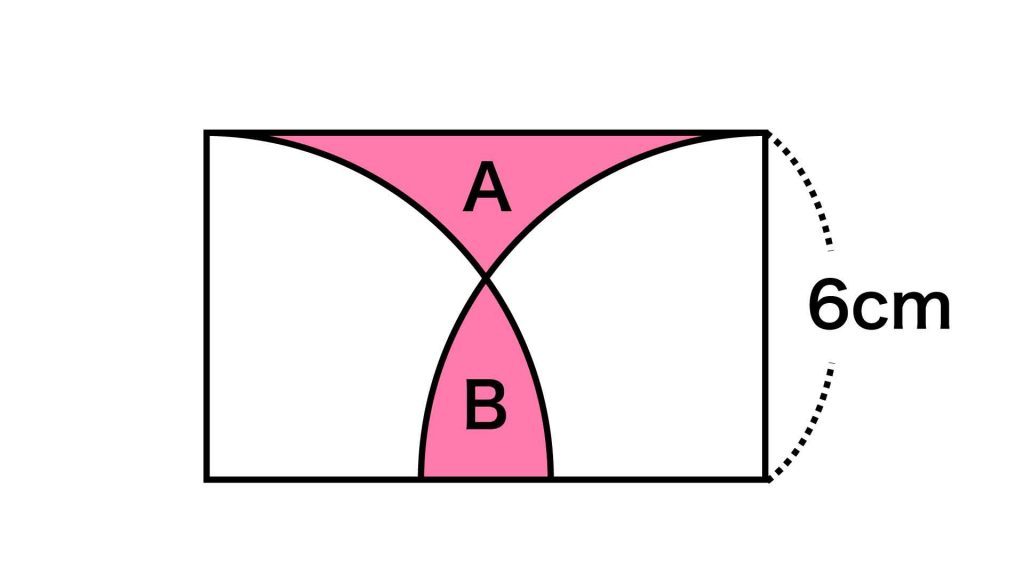
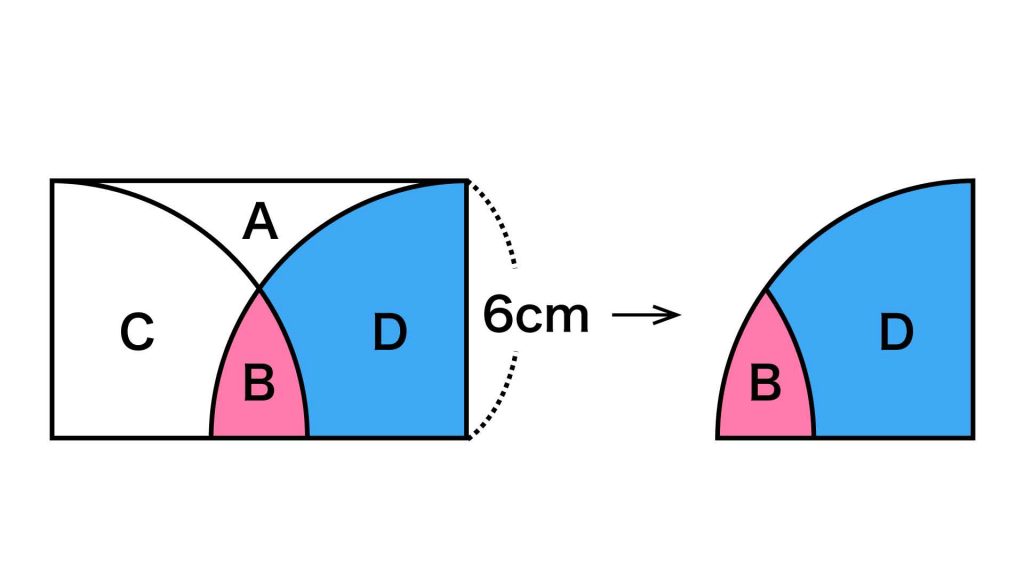
BとDを組み合わせた図形に注目すると、この図形は半径が6cm、中心角が90度の扇形であることがわかります。

したがって、B+Dの面積は、6×6×π÷4=9πcm²です。

長方形の面積は扇形2つ分

長方形の面積は、B+Dの面積を2倍することで求めることができます。

したがって、長方形の面積は、9π×2=18πcm²となります。

答え：18πcm²

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】