解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
▲以下の解説では、問題の図を再現したこちらの図を使用します
前ページ：【解答フォーム】自力で解きたい方はこちらへ！ 以下は問題の答えです
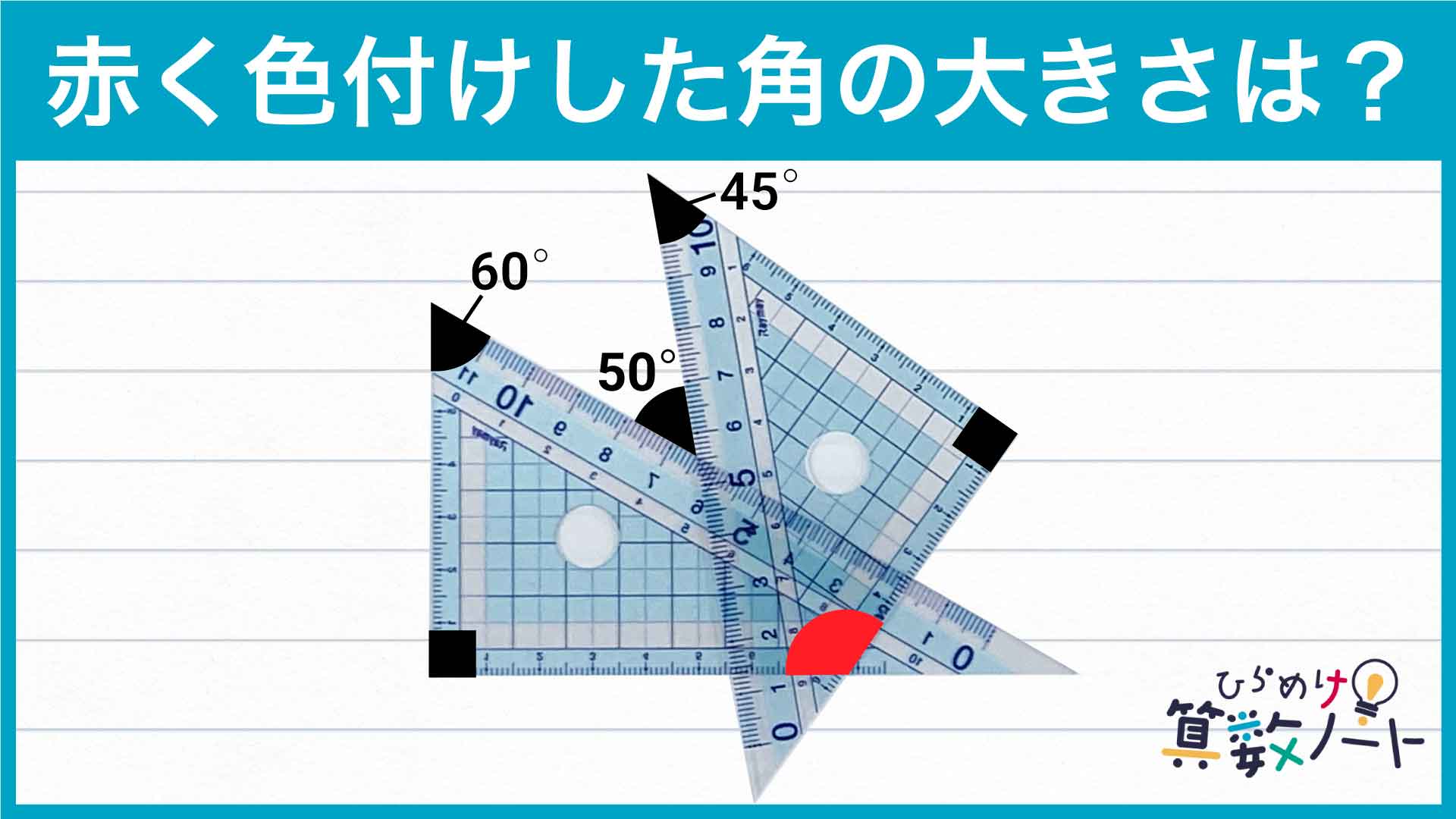
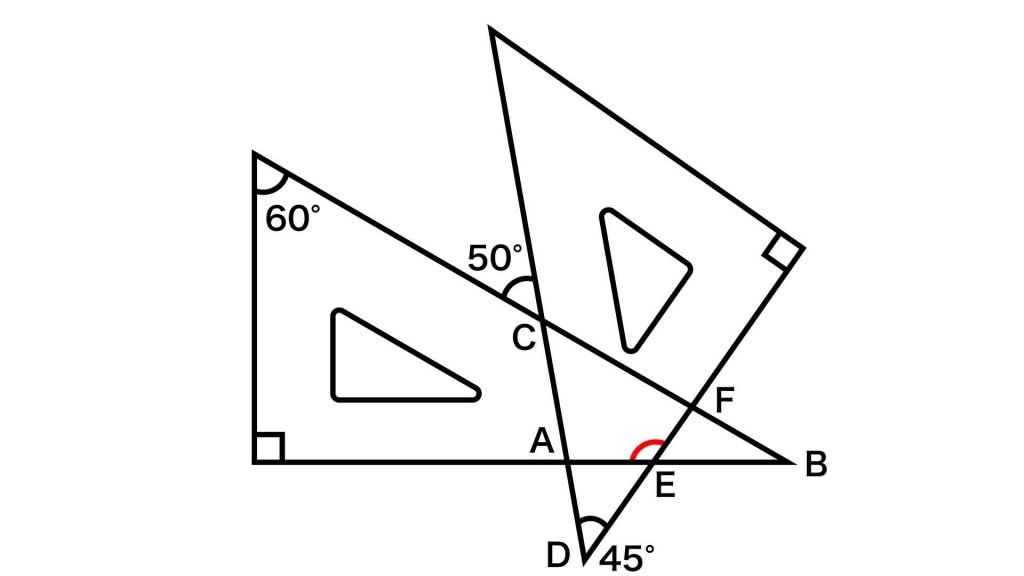
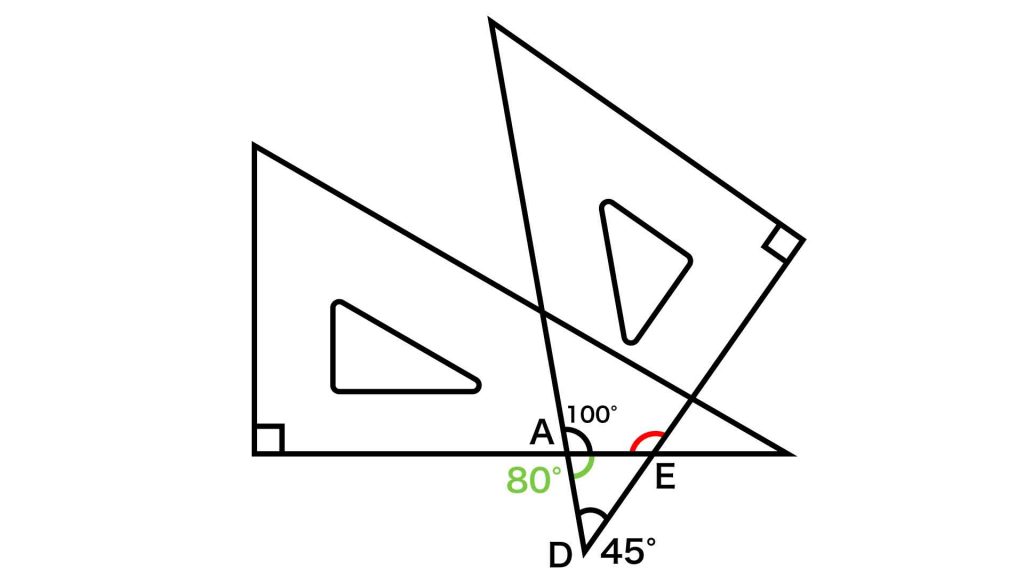
下の図のように記号を振り、解説します。
三角形ABCに着目する
まず、三角形ABCに着目します。
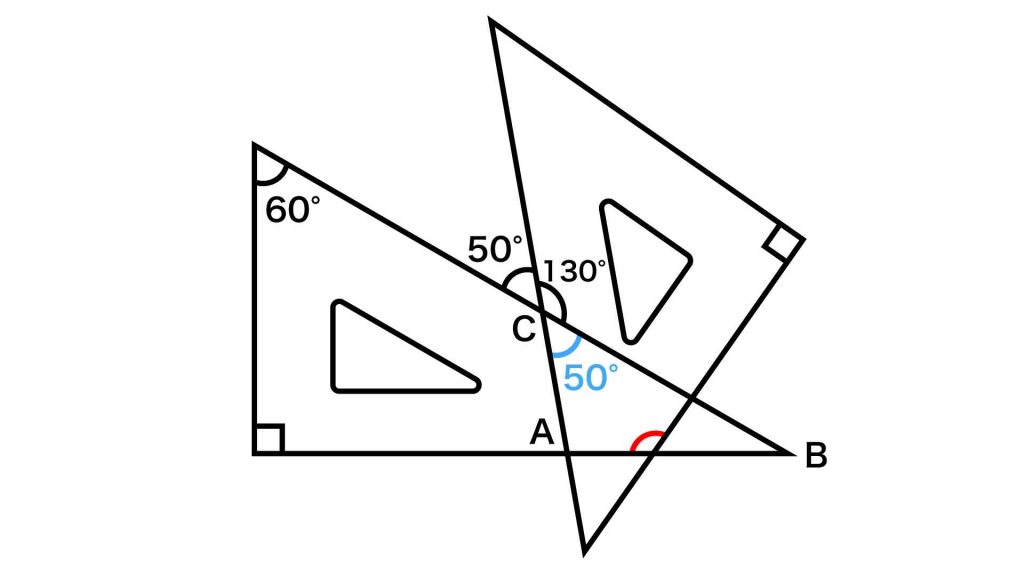
角ACBに隣り合う角の大きさは180-50=130度なので、角ACBの大きさは180-130=50度となります。
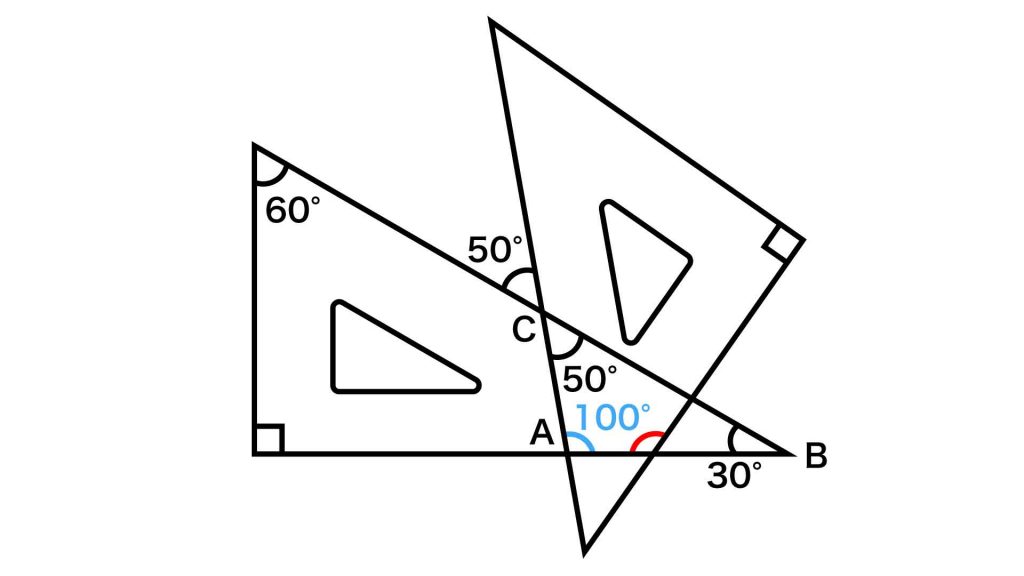
図形が三角定規であることを踏まえると、角ABC=180-90-60=30度です。三角形の内角の和は一定（180度）のため、角CAB=180-(50+30)=100度となります。
三角形ADEに着目する
次に、三角形ADEに着目します。
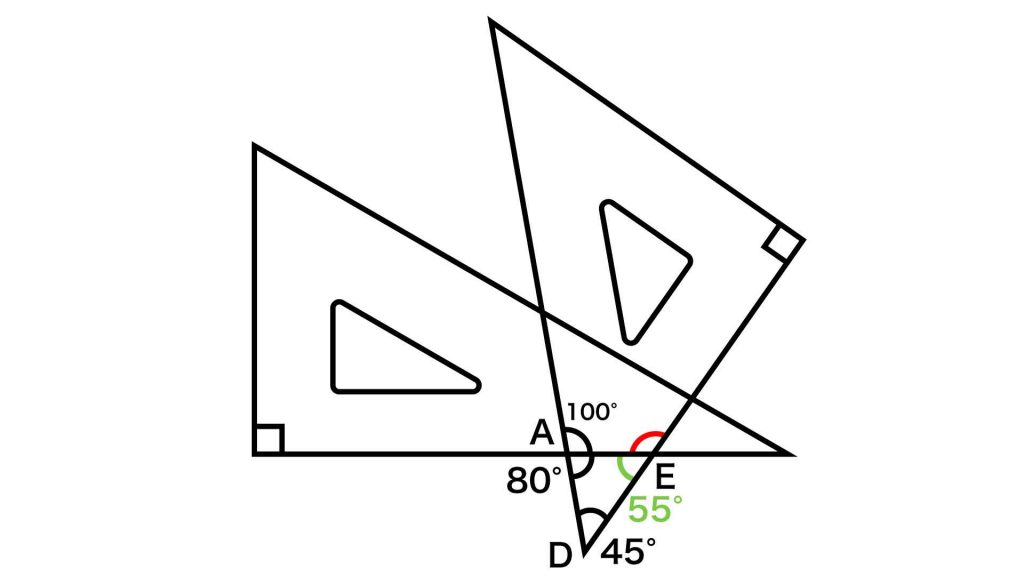
角DAE=180-角CAB=180-100=80度です。
三角形の内角の和は一定（180度）のため、角AED=180-(80+45)=55度です。
以上より、赤く色をつけた角の大きさは、180-55=125度となります。
答え：125度
中学校で習う「外角の定理」を使えばもっと簡単に解ける！
「外角の定理」は、「三角形の外角の大きさは、その外角と隣り合っていない2つの内角の大きさの和に等しい」という定理です。
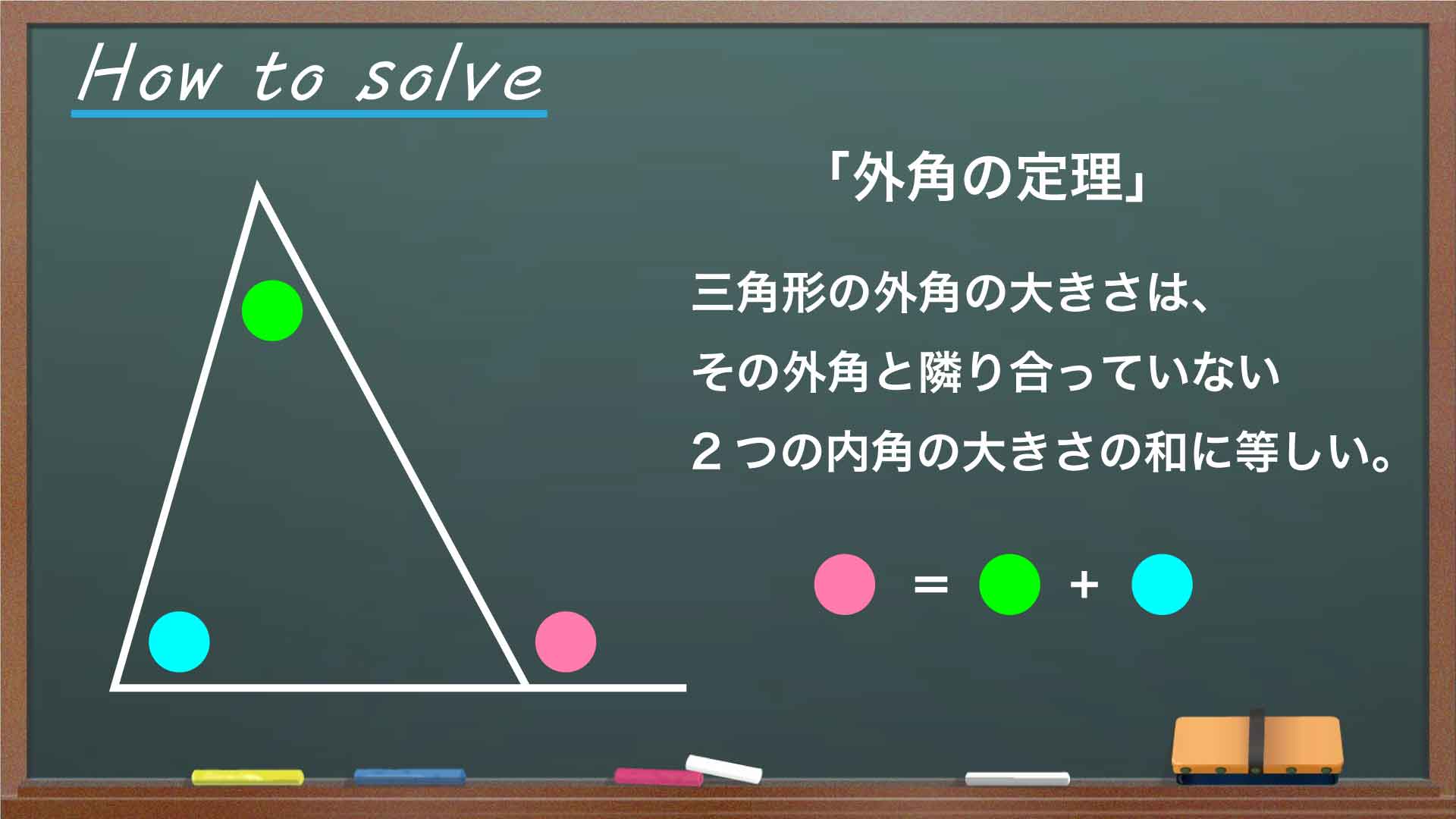
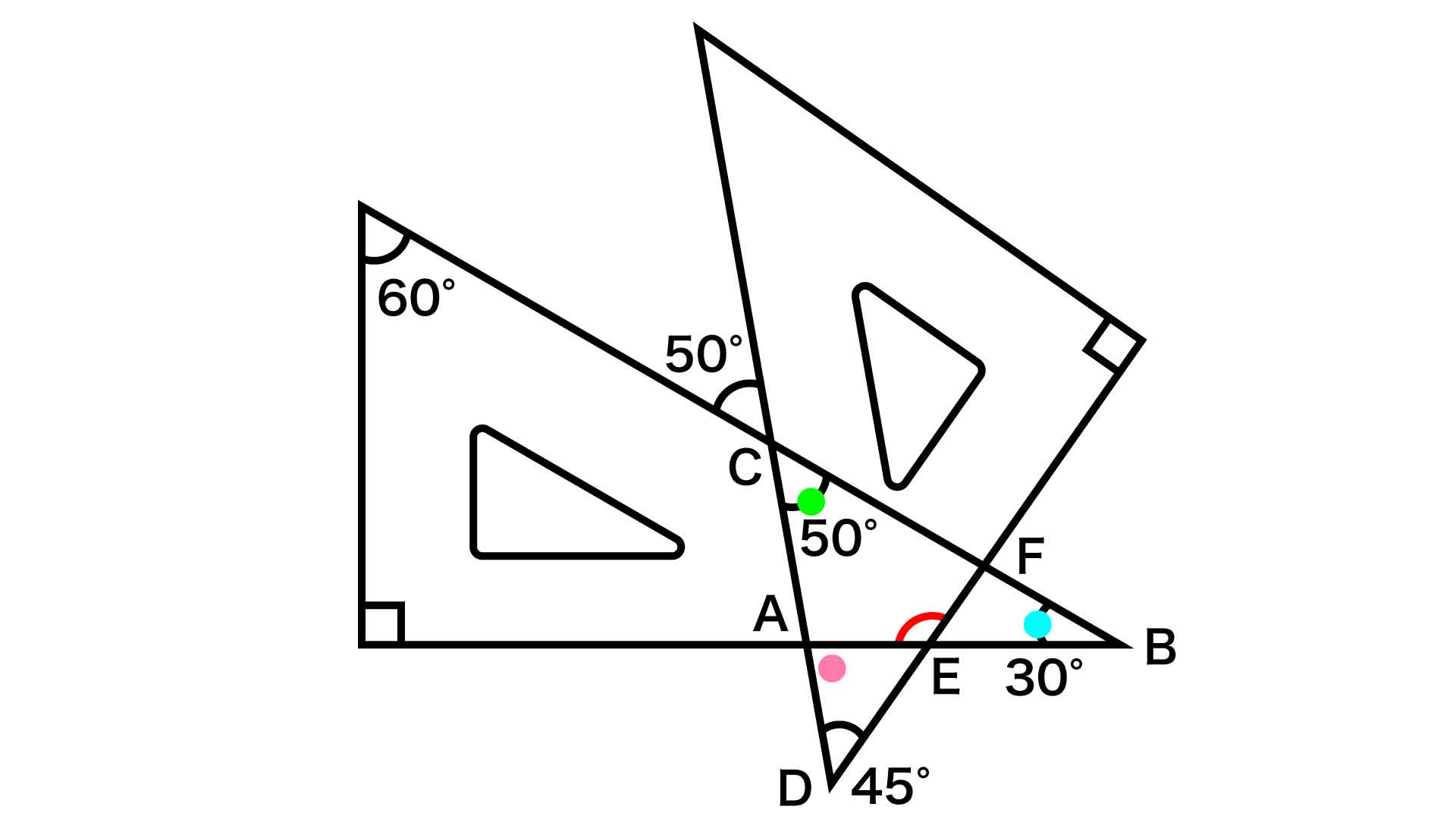
外角の定理を使うと、今回の問題は以下のように解くことができます。
角DAEは三角形ABCの外角であるため、外角の定理より、角ABC+角ACB=30+50=80度とわかります。
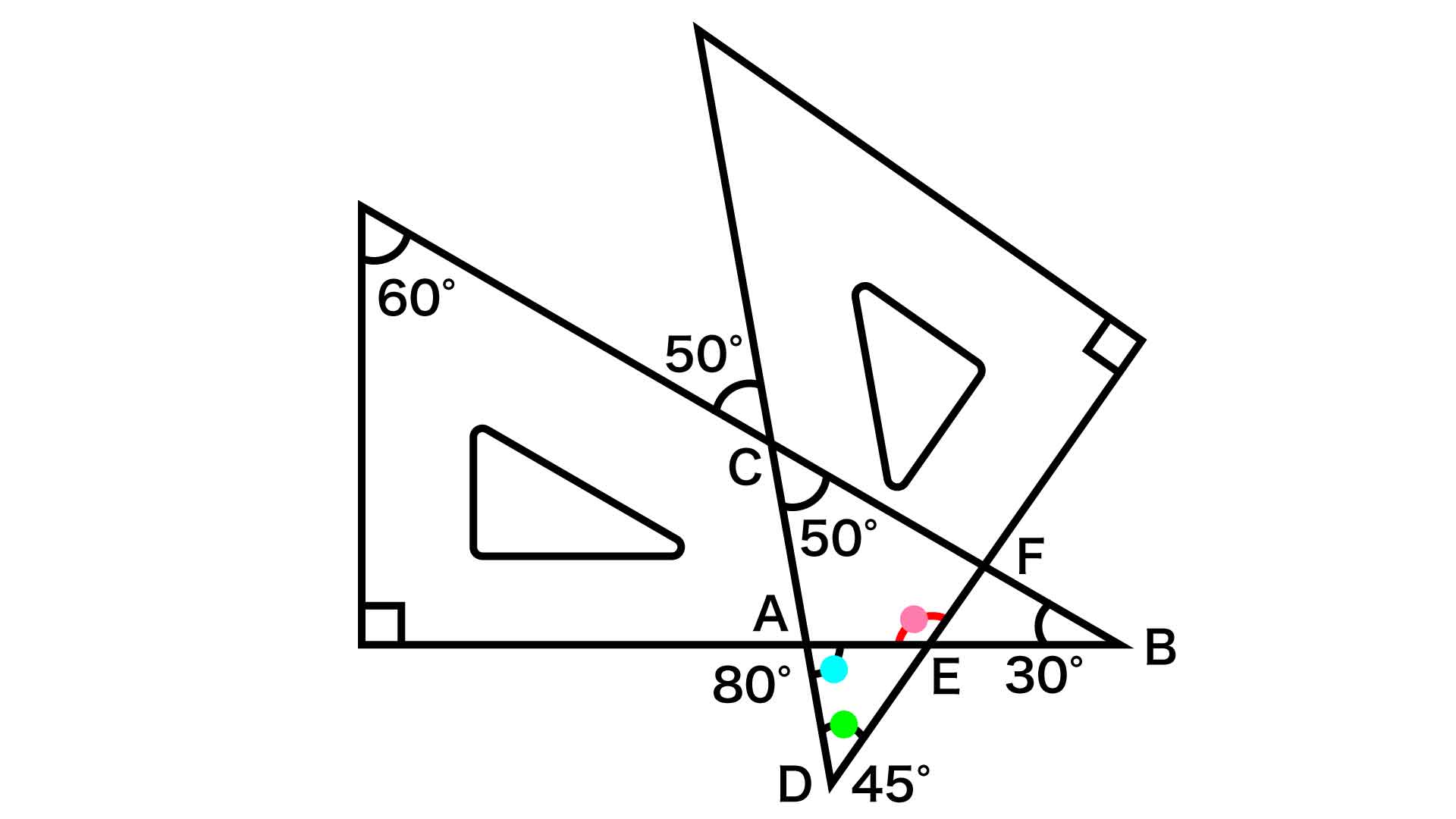
同様にして、赤く色をつけた角は三角形ADEの外角なので、外角の定理より、角ADE+角DAE=45+80=125度と求めることができます。
それではまた次の算数ノートでお会いしましょう！
「ひらめけ！算数ノート」のバックナンバーはこちらから！
【前回の算数ノートはこちら】
【あわせて読みたい】
