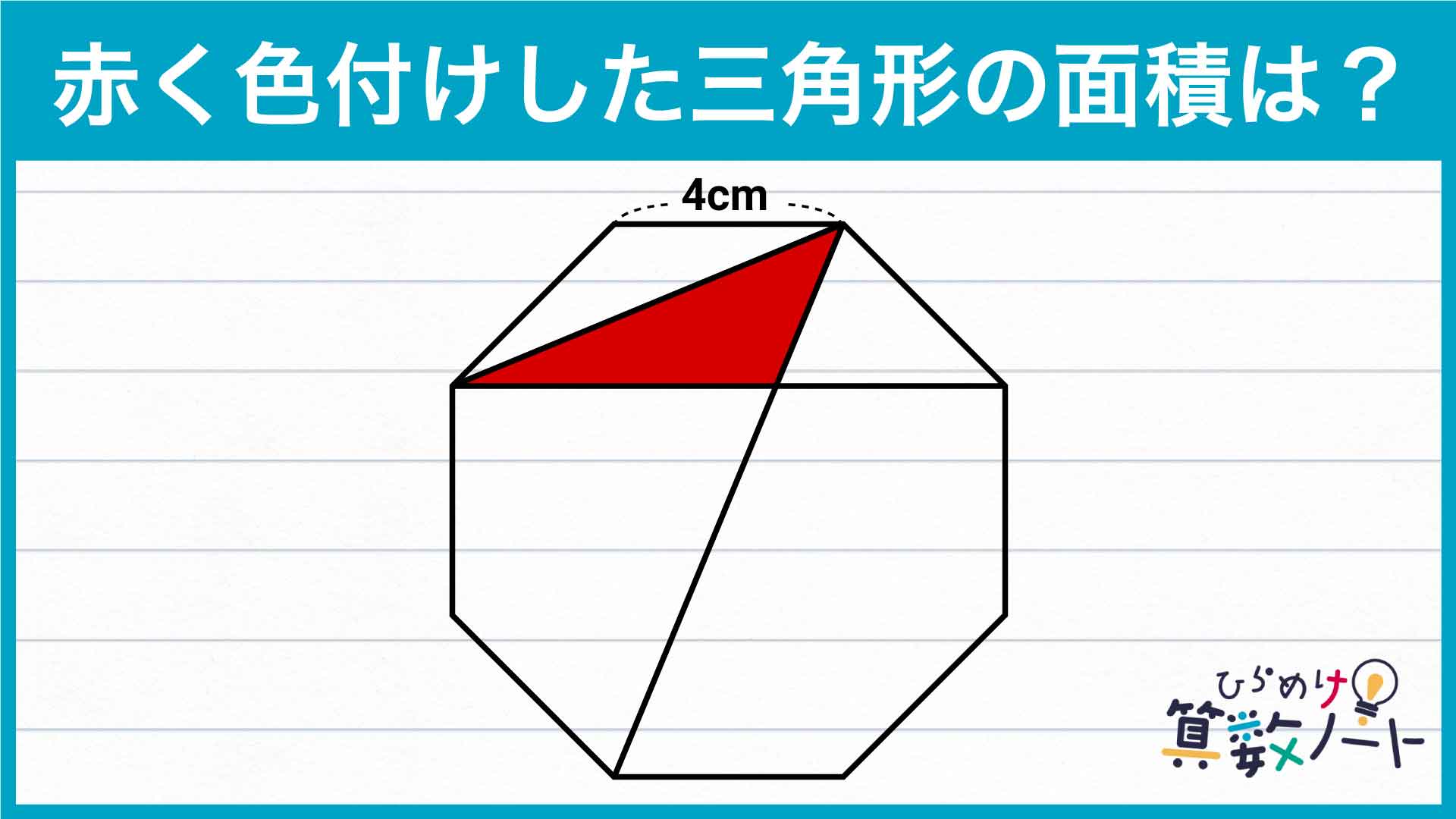
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
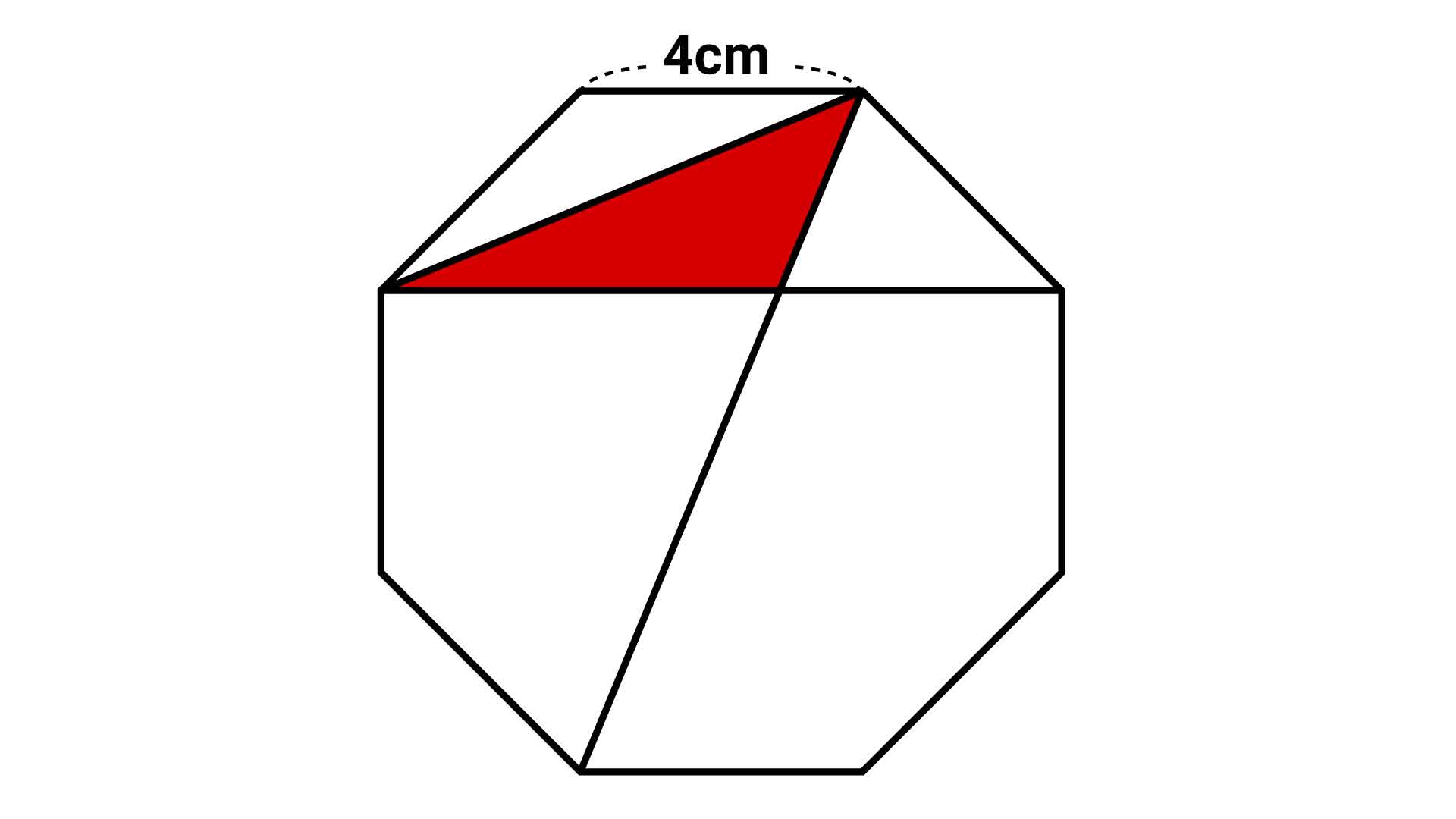
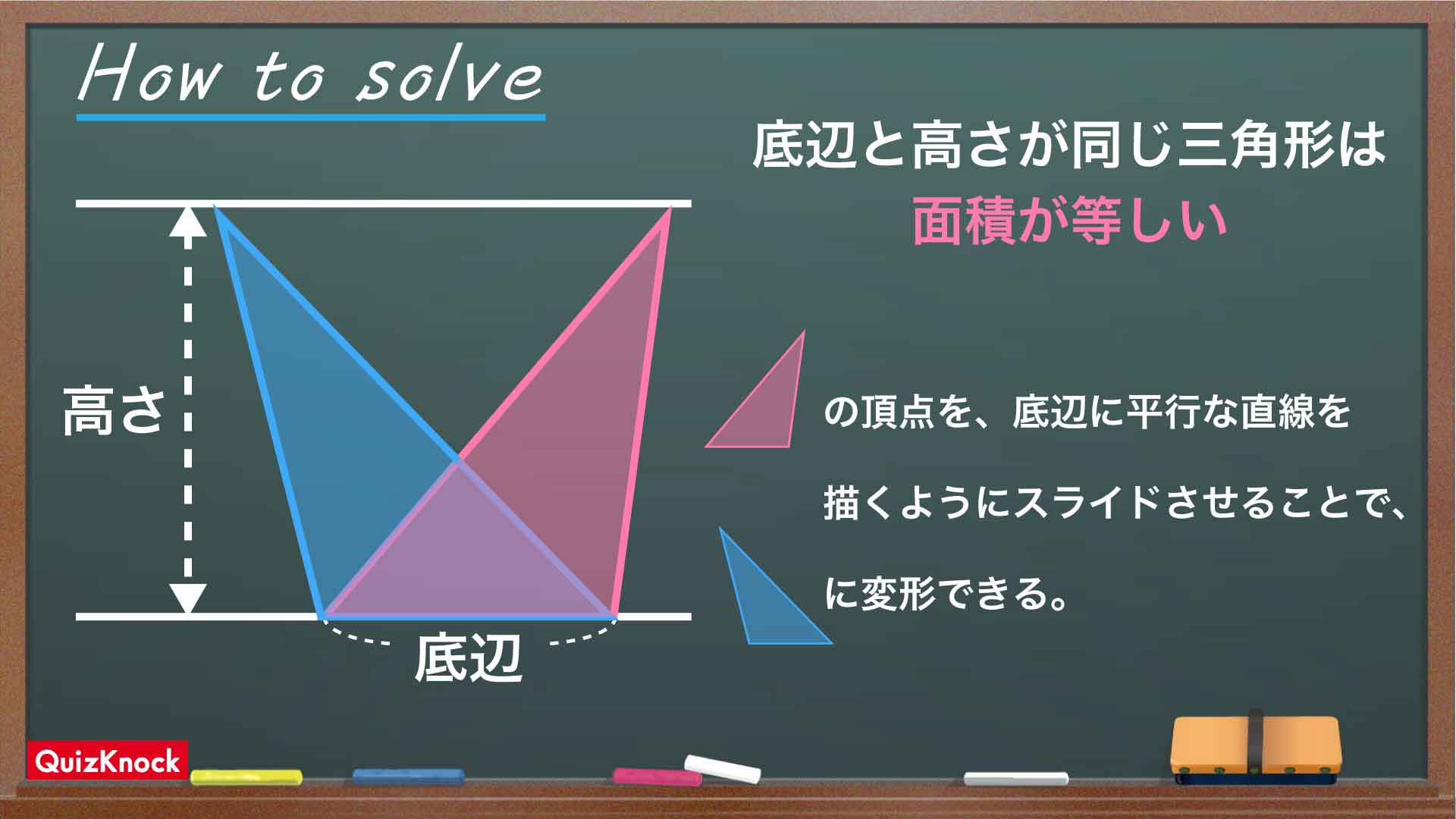
今回のポイントは、「三角形を同じ面積のまま変形させる」ことです。
底辺が同じ三角形どうしは、高さが等しい限り同じ面積になるため、底辺と高さを固定して三角形を変形させることが可能です。
以上を踏まえ、問題を解いていきましょう!
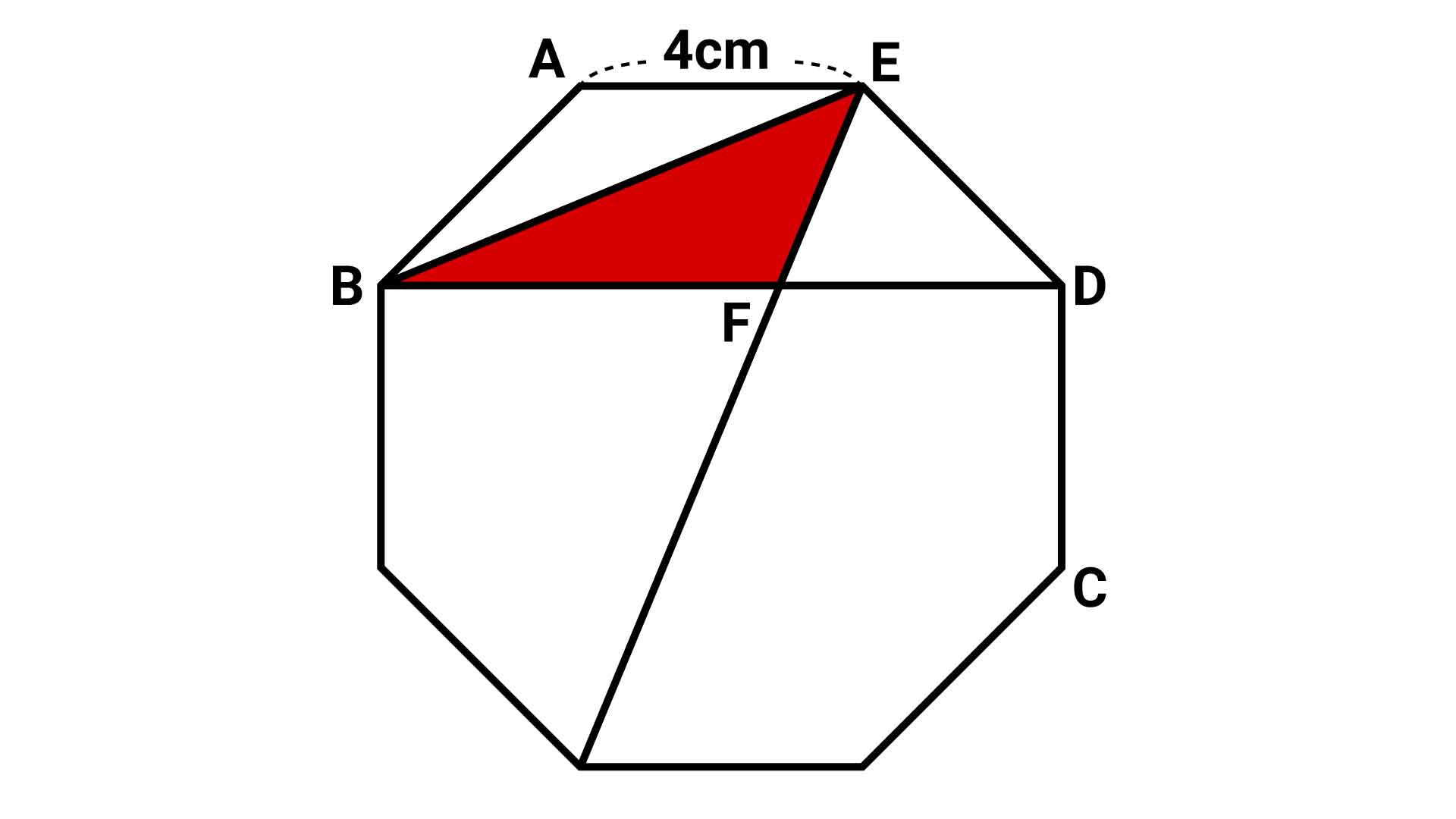
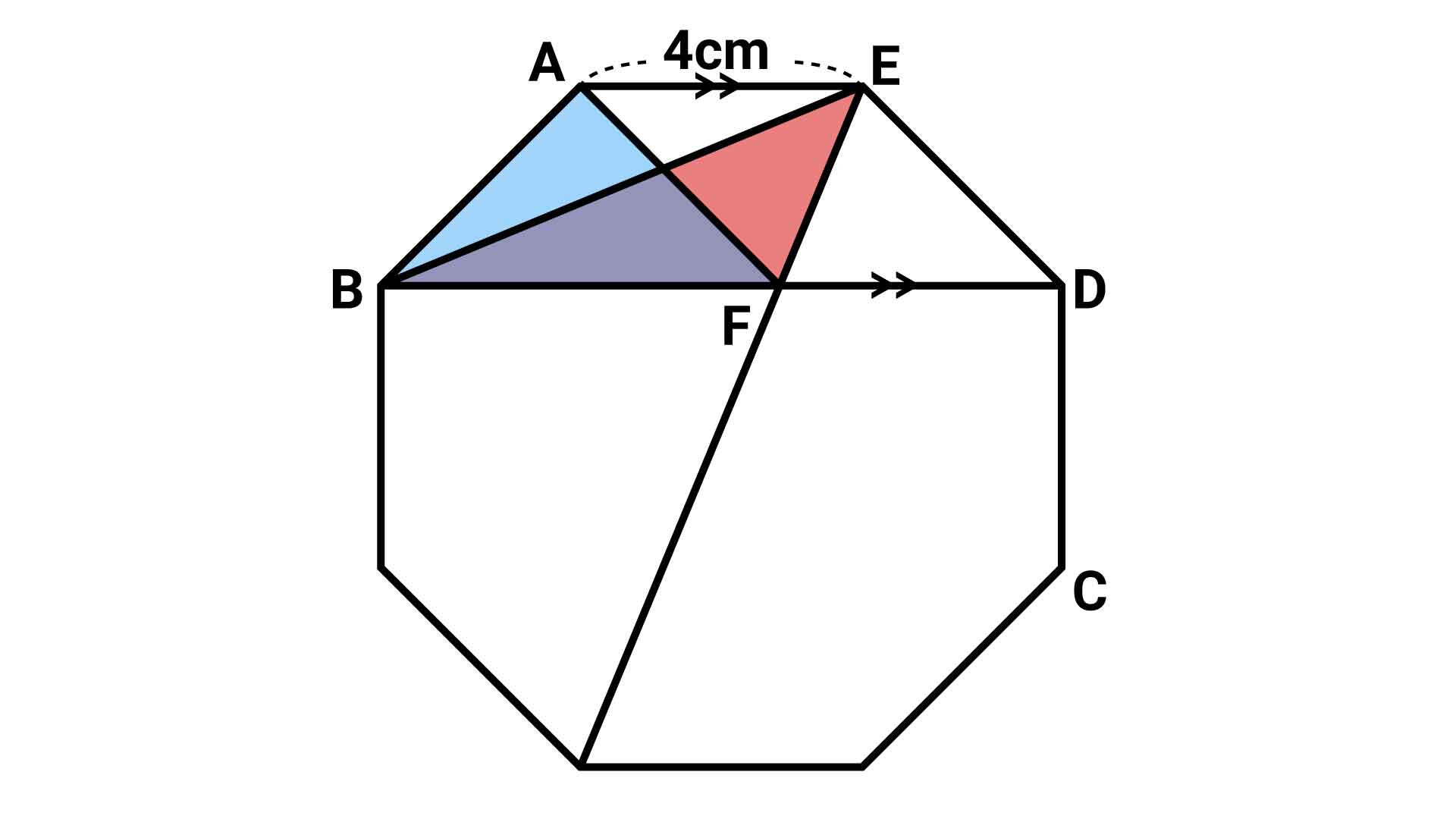
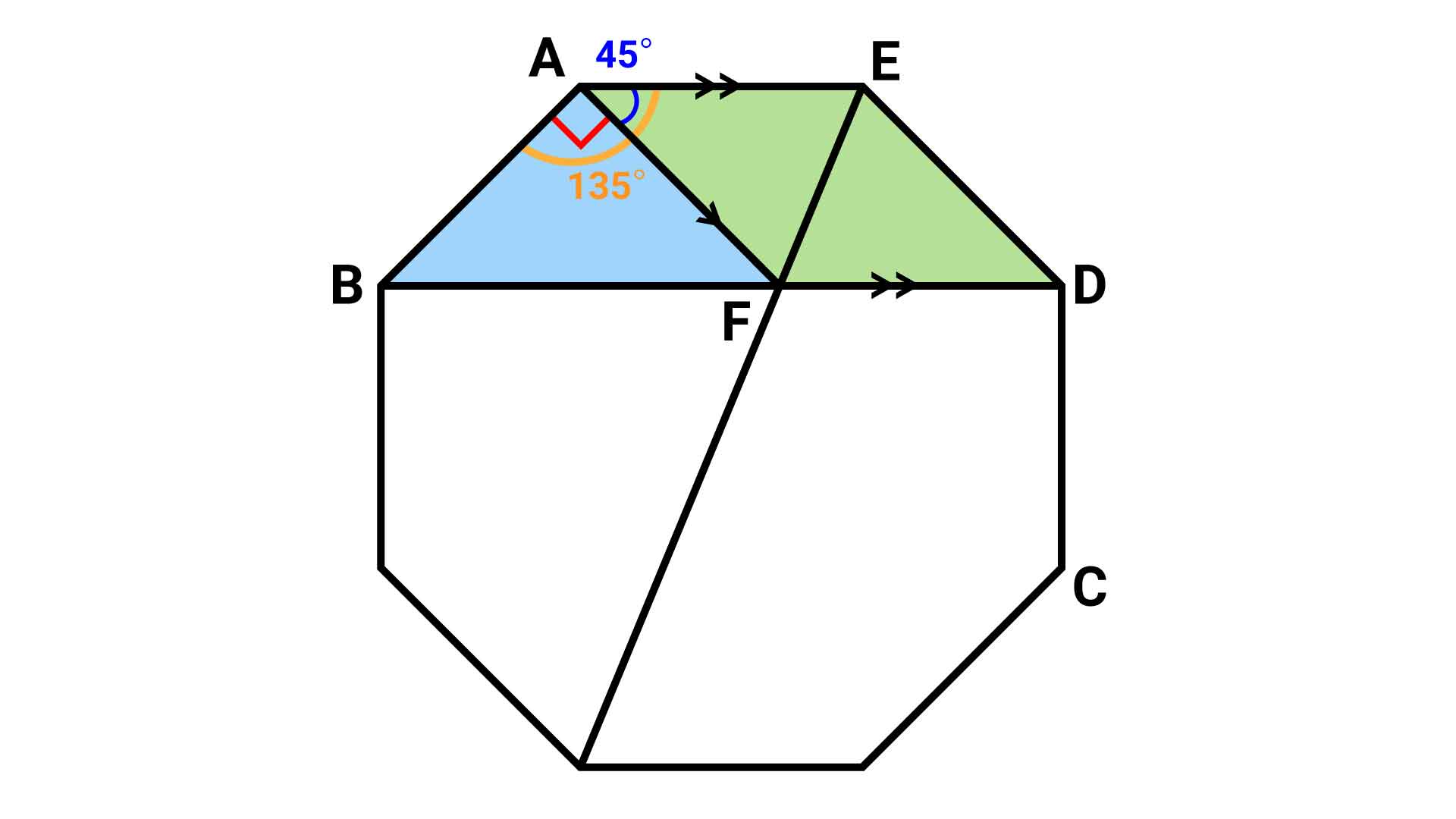
以下、説明をしやすくするため、図形にA~Fまでの記号をふります。
赤い三角形を変形する
正八角形の性質として、辺AEと対角線BDは平行になります。したがって、先ほどの“How to solve”で説明した性質を赤い三角形EBFに適応させると、赤い三角形を同じ面積のまま青い三角形ABFへと変形させることができます。
以降は、この青く塗った三角形ABFの面積を求めていきます。
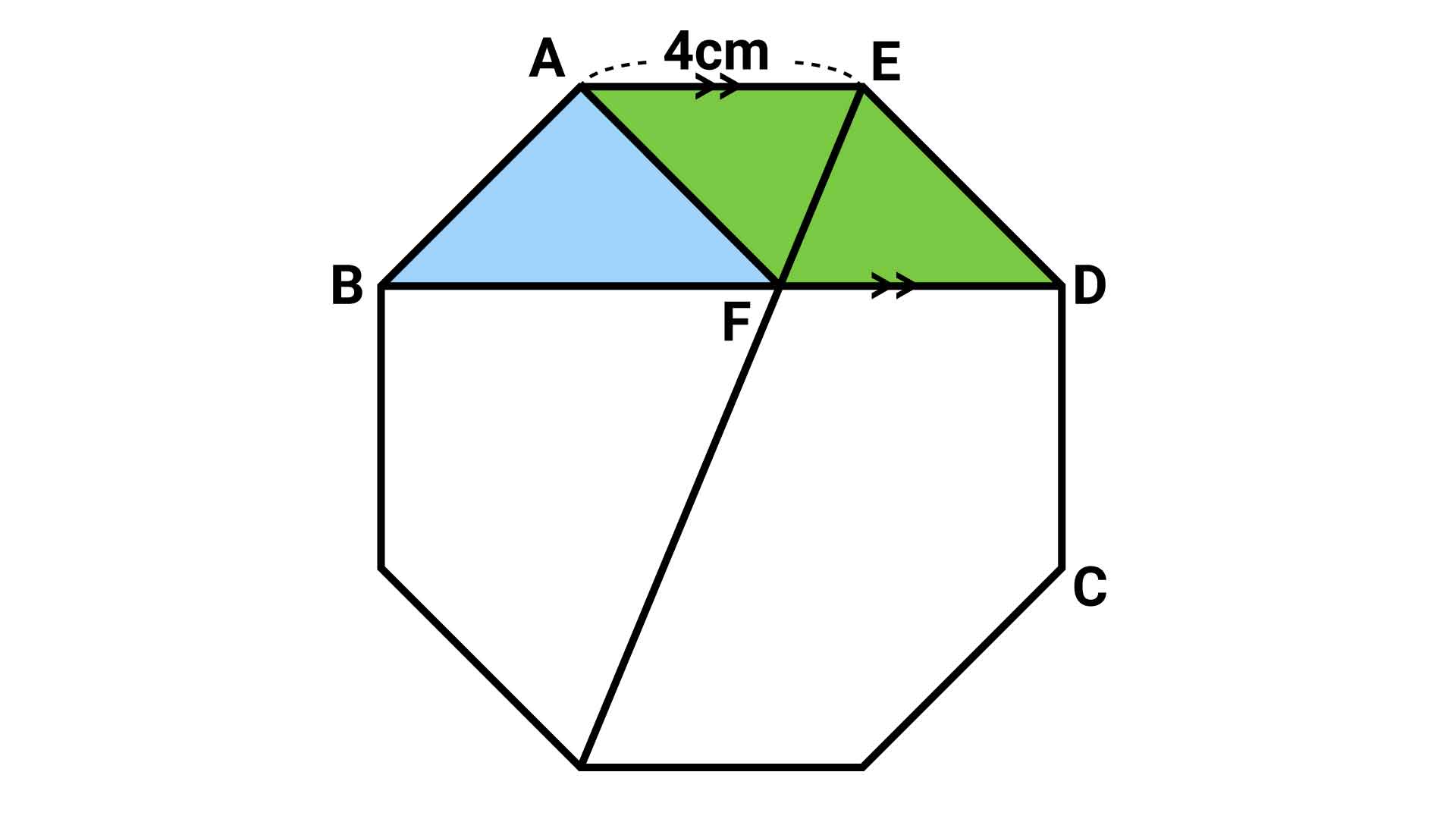
右隣の四角形の着目する
青い三角形ABFの右隣にある、緑色の四角形AFDEに注目してください。この四角形が、三角形ABFの面積を求めるカギになります。
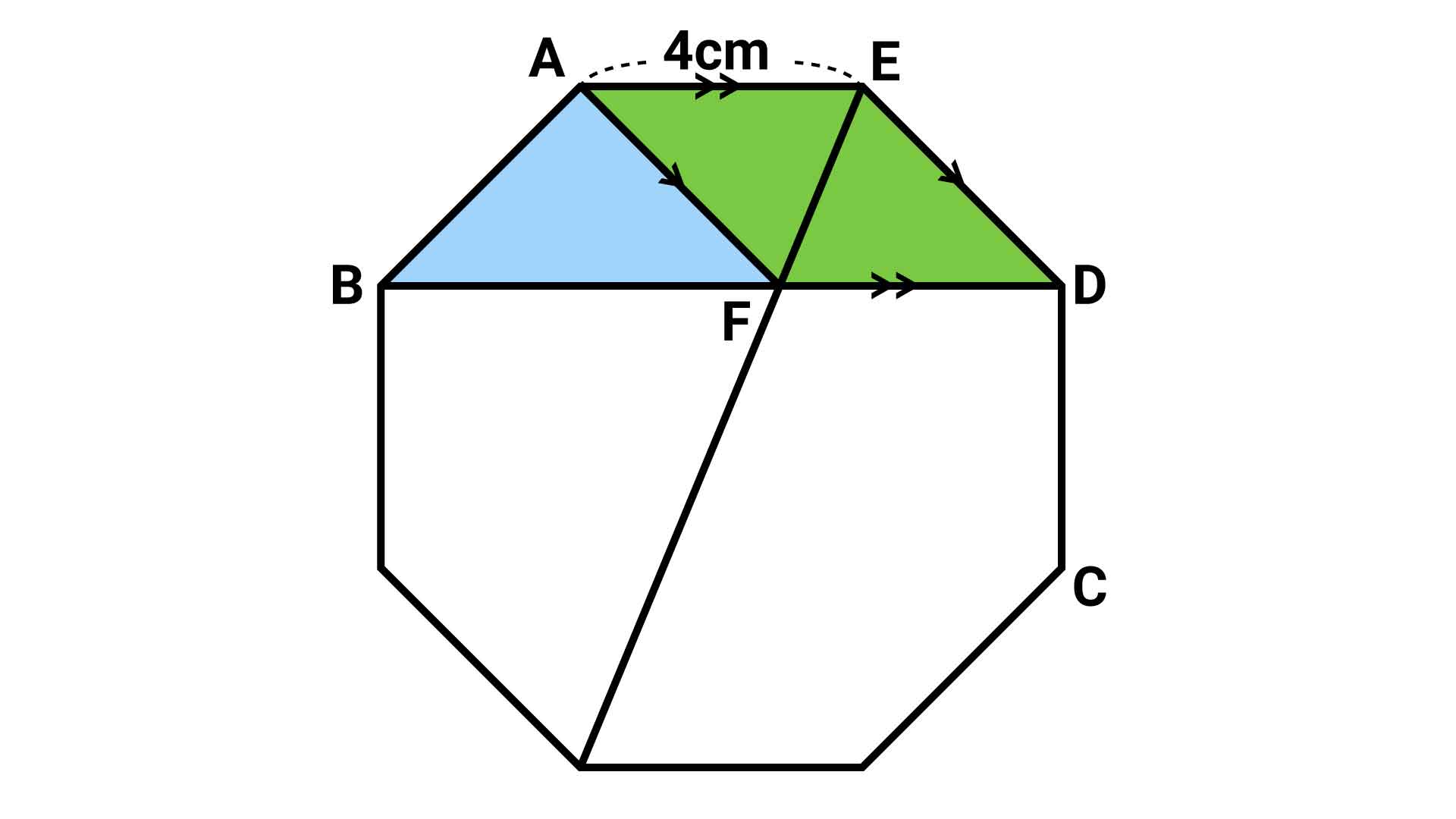
また、対称性より直線AC上にFがあるので、、辺EDと辺AFも平行の関係にあります。
したがって、四角形AFDEは、辺EDと辺AF、辺AEと辺FDがそれぞれ平行の関係にあることがわかります。ここで、以下に示す性質を適応させます。
この性質から、緑色の四角形AFDEは平行四辺形であり、向かい合う辺の長さや角の大きさが等しくなることがわかります。
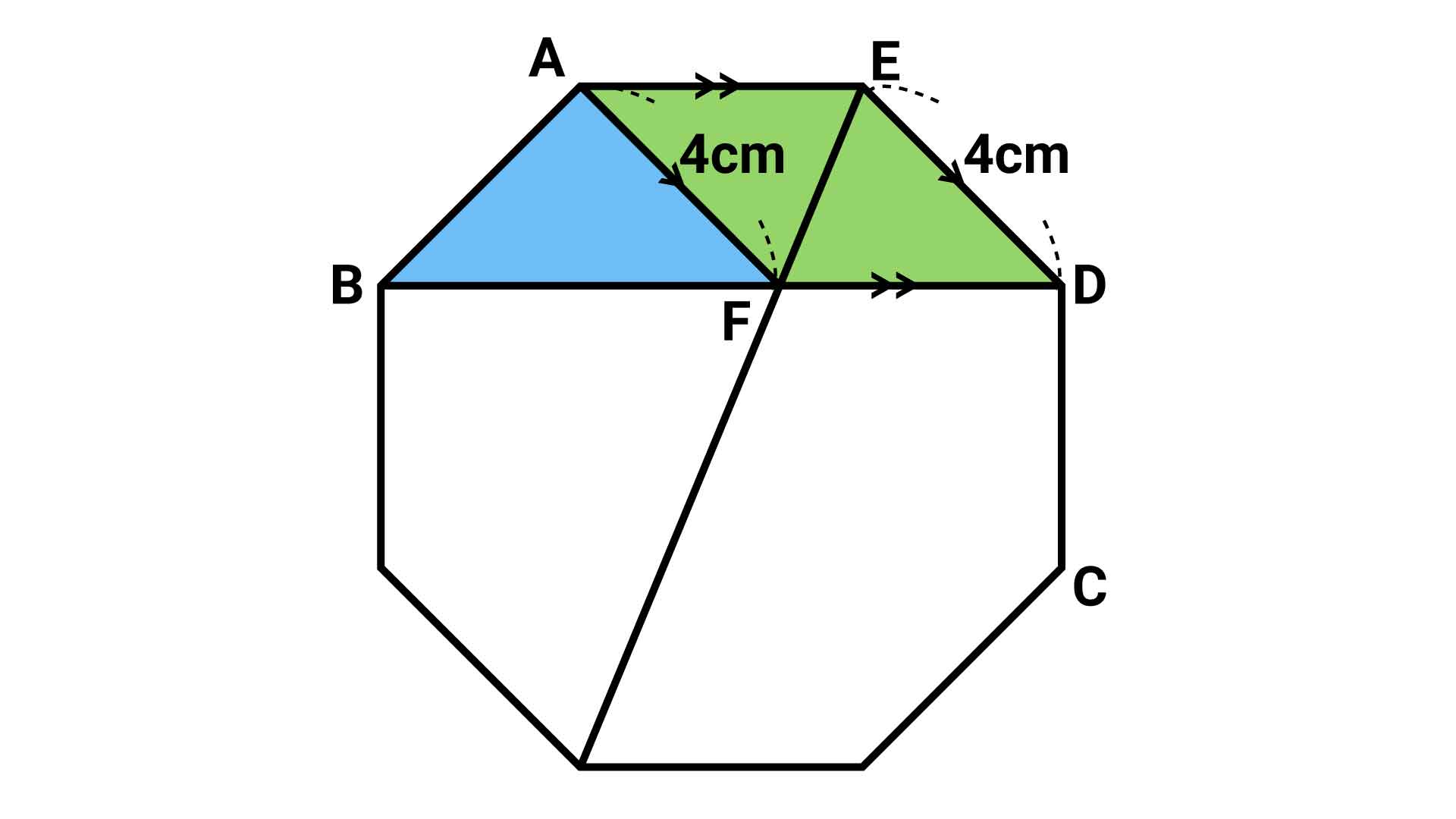
以上より、辺AFの長さが4cmであることがわかります。
また、緑色の平行四辺形AFDEの内角も、それぞれ求めることができます。
多角形の内角の和は、「180×(辺の数-2)」という式で求めることができるので、正八角形の1つの内角の大きさは、180×(8-2)÷8=135度となります。 これにより、緑色の平行四辺形AFDEの2つの角AED、AFDの大きさはそれぞれ135度となり、残る2つの角EAF、EDFの大きさは(360-135×2)÷2=45度となります。
角BAEの大きさは135度であることから、青い三角形ABFの1つの内角BAFは、135−45=90度(直角)となります。
青い三角形の面積を求める
以上を踏まえると、青く塗った三角形ABFは、4cmの辺を2本もつ直角二等辺三角形であることがわかります。
青い三角形ABFの面積が4×4÷2=8cm2であることから、元の赤い三角形EBFの面積も8cm2となります。
答え:8cm2
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】













.jpg)









.jpg)







