解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
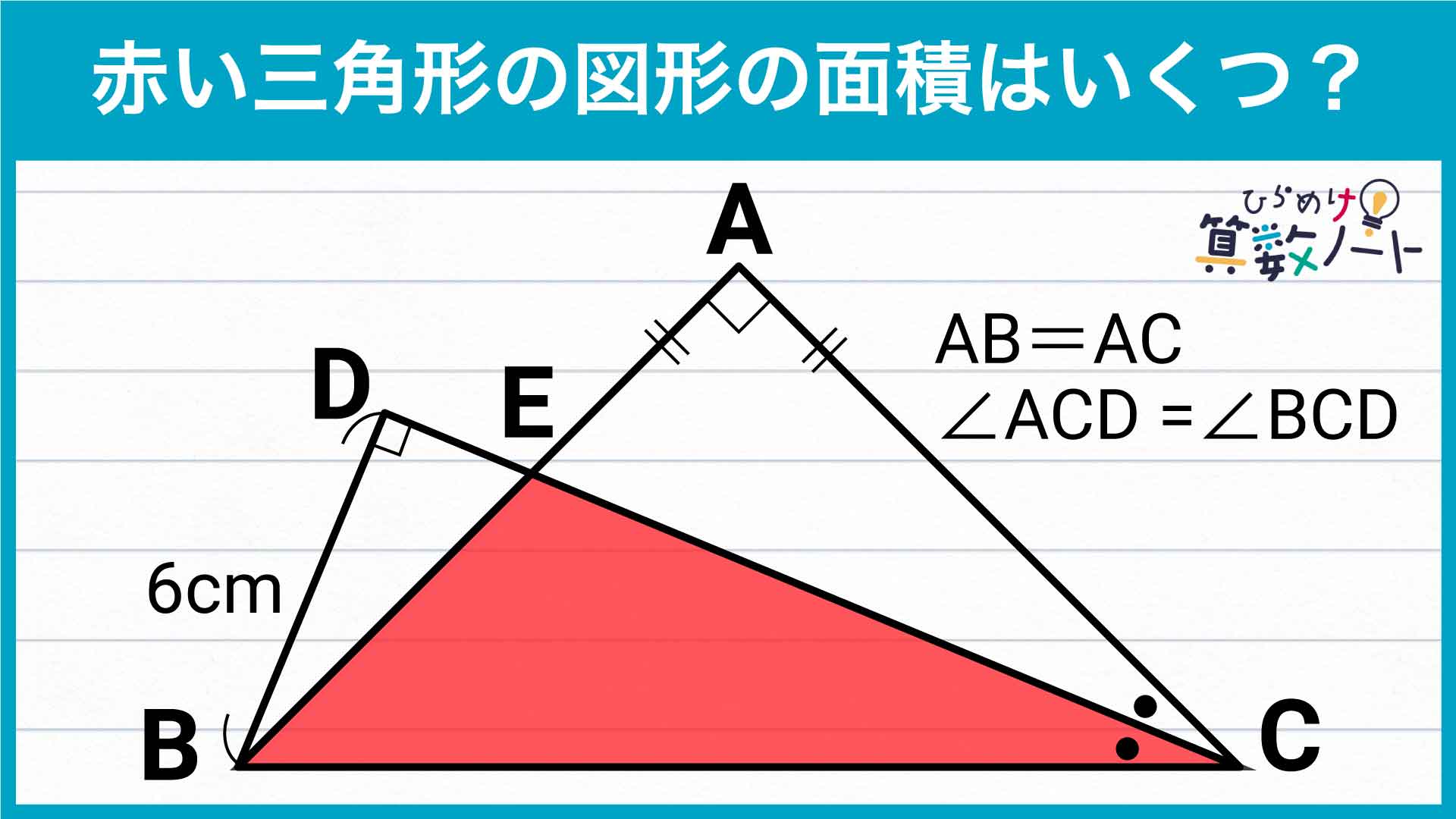
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
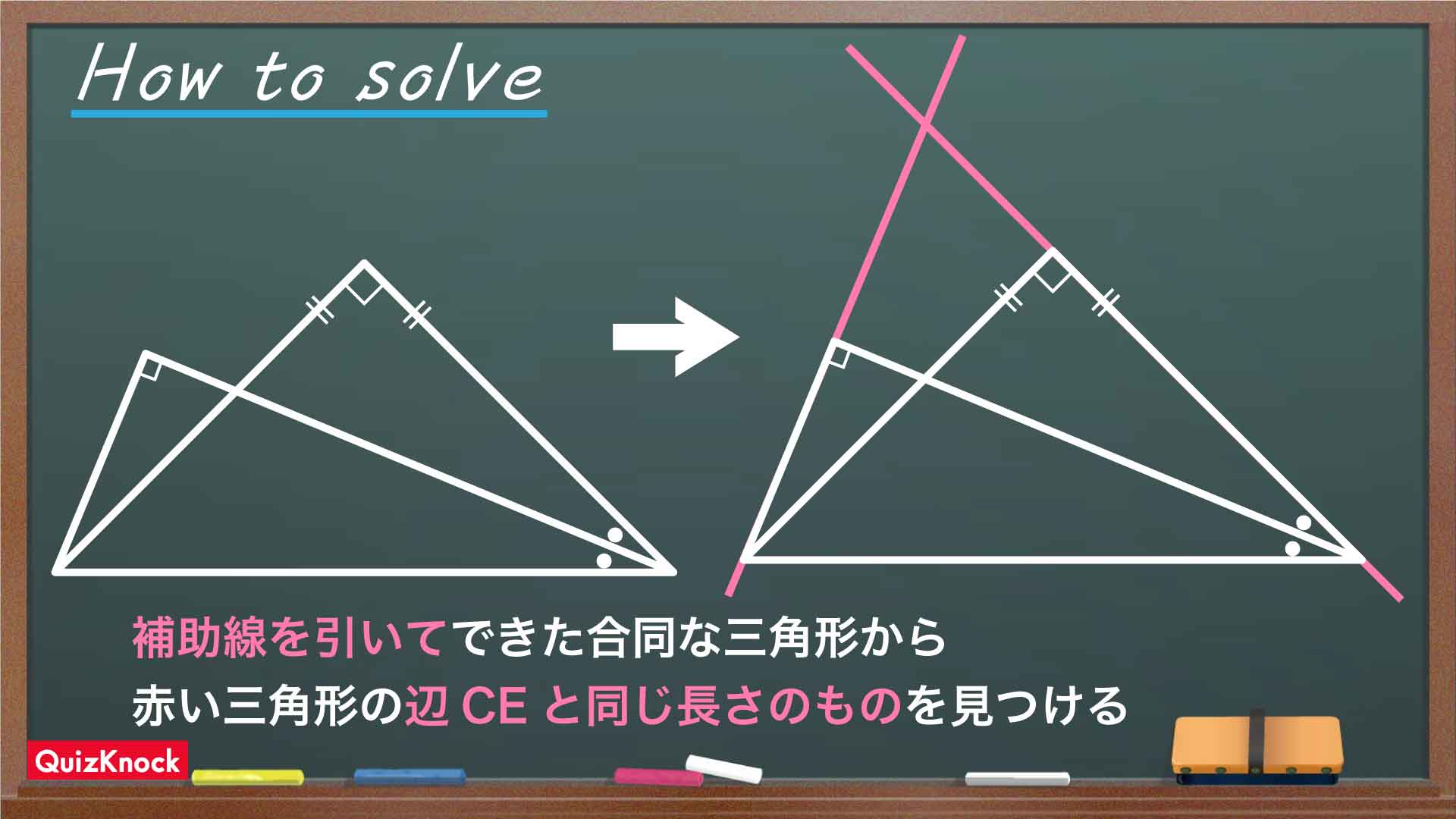
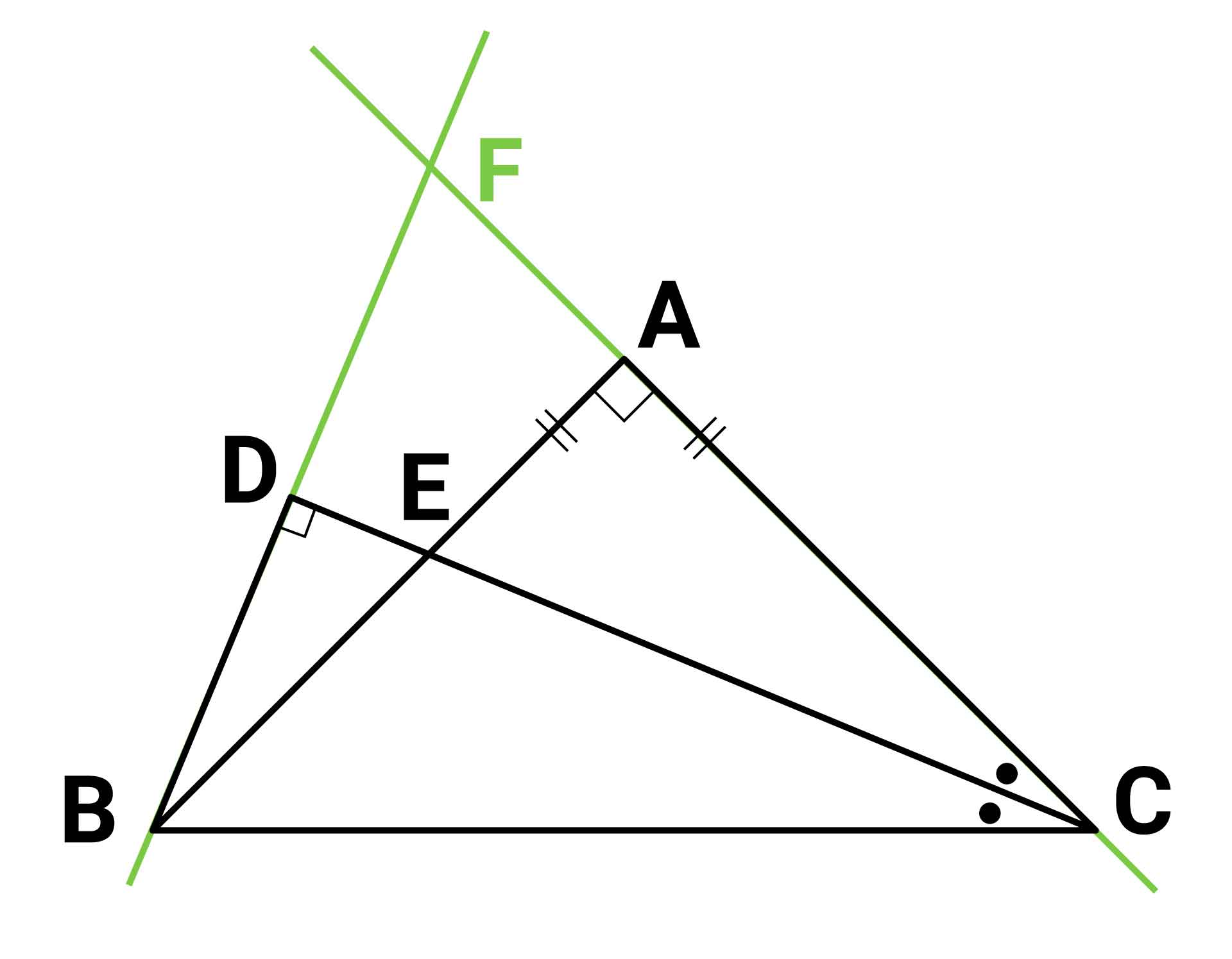
今回の問題の解き方をまとめた図がこちらです。ポイントは補助線を引いて合同な三角形を見つけることです。
この図の流れに沿って、解いていきましょう!
補助線を引く
まず、直線ACと直線DBを引き、2つの直線の交点を点Fとします。
補助線を引いたことで、三角形の数が増えました。ここから辺CEと同じ長さになるものを探していきます。
同じ大きさの角を探そう!
それぞれの三角形の性質を調べるために、同じ大きさの角を探してみましょう。
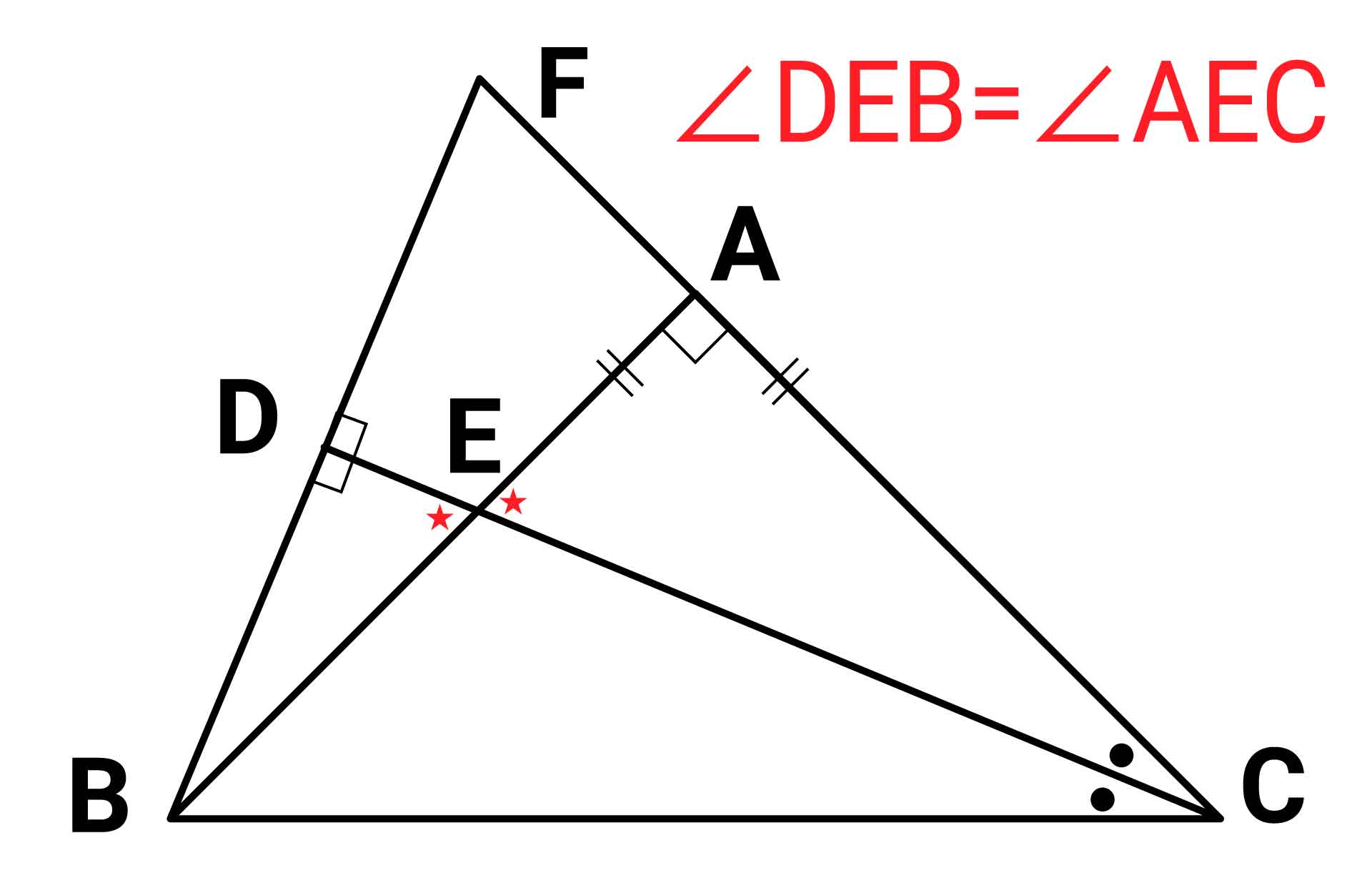
角DEBと角AECは互いに向かい合っているため、角DEB=角AECです。
ここで、三角形DBEに着目します。三角形の内角の和が180度であることから、角DBE=180度-90度-角DEB=90度-角DEBとなります。
また、三角形ACEに着目すると、三角形の内角の和が180度であることから、角ACE=180度-90度-角AEC=90度-角AECとなります。
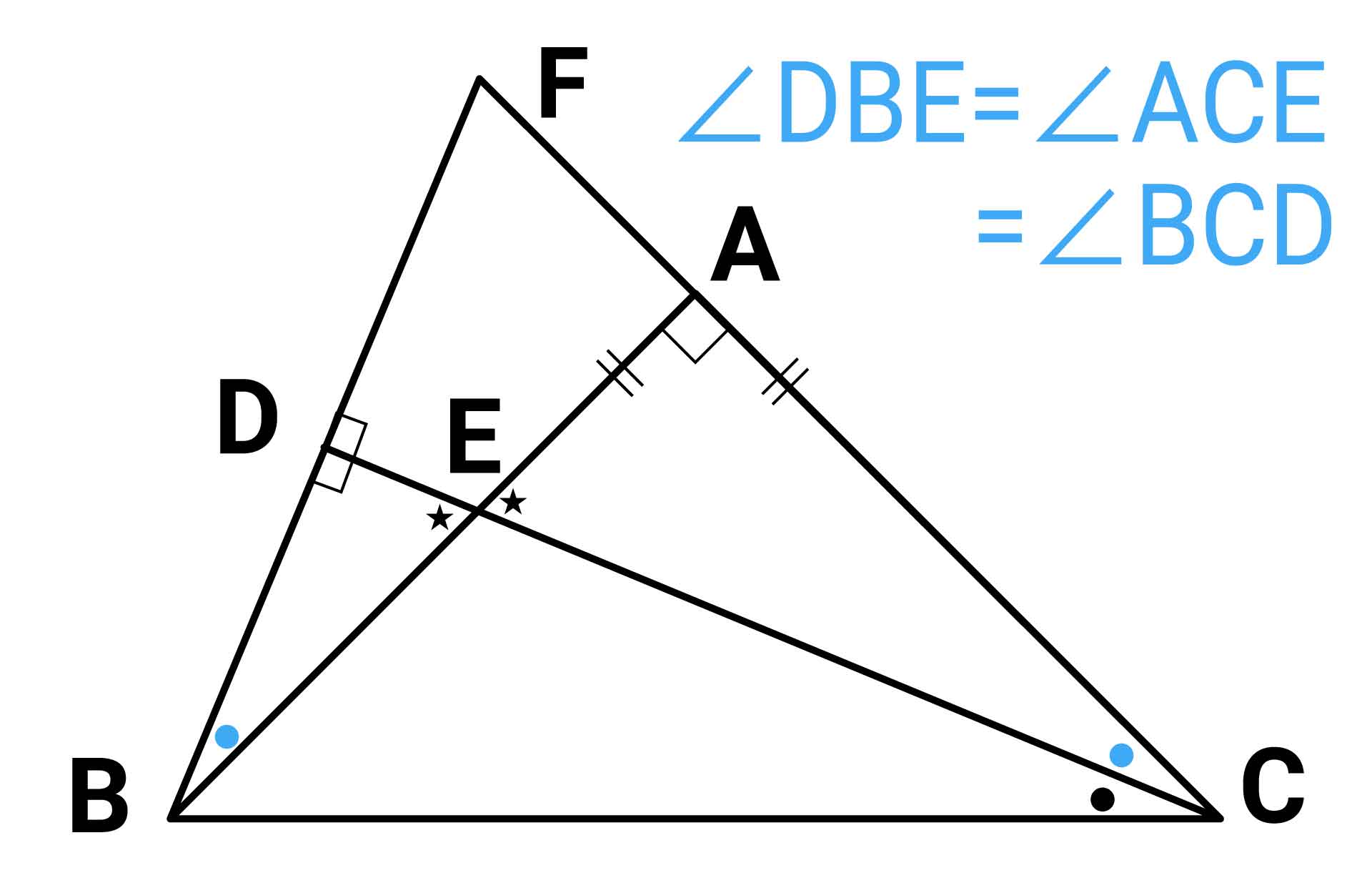
以上より、角DEB=角AECであることから、角DBE=角ACE(=角BCD)であることがわかります。
合同な三角形は?
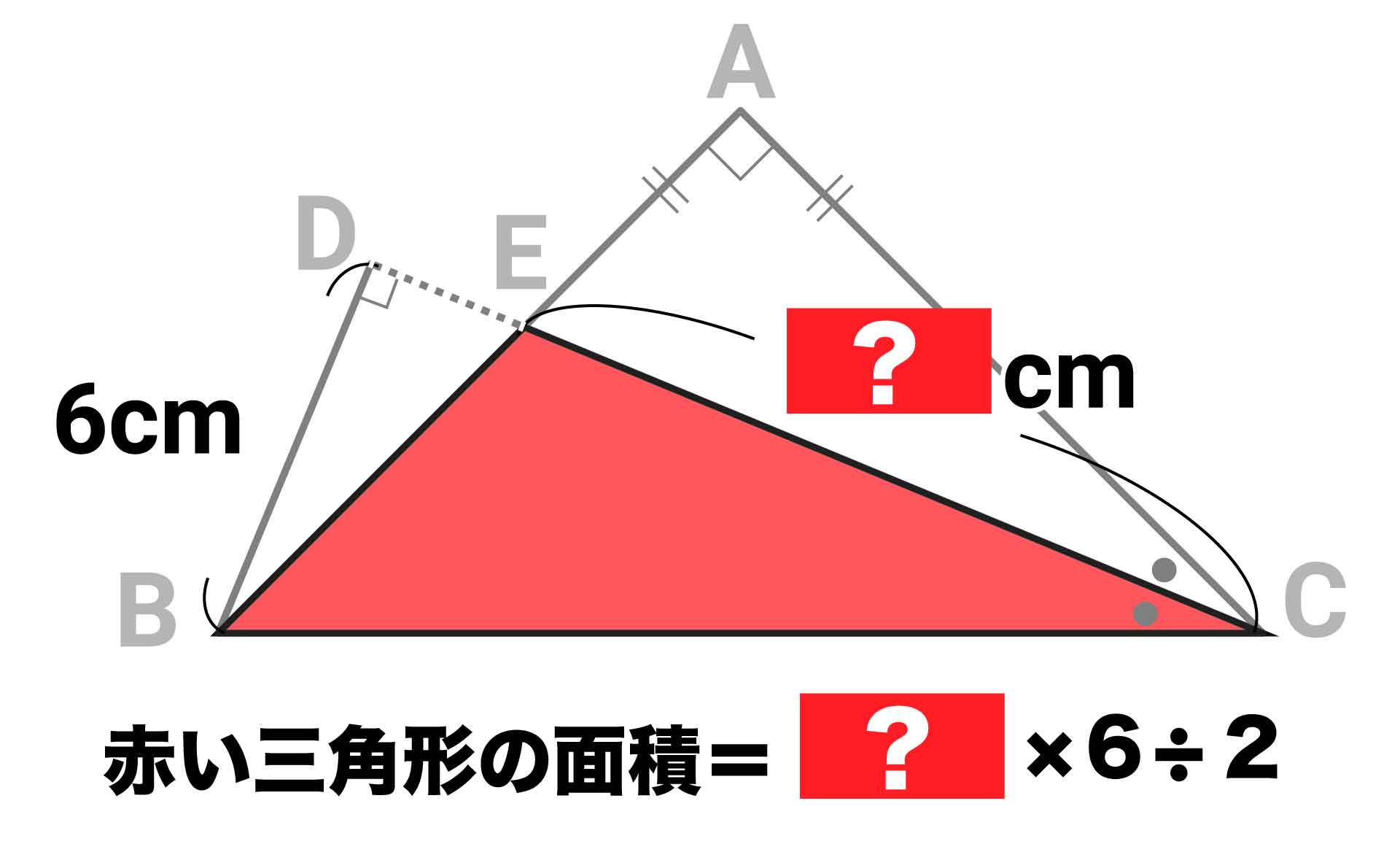
三角形BCEの面積を求めるには、辺CEの長さを知ることが必要になります。辺CEの長さを知るために、合同な三角形を探していきましょう。
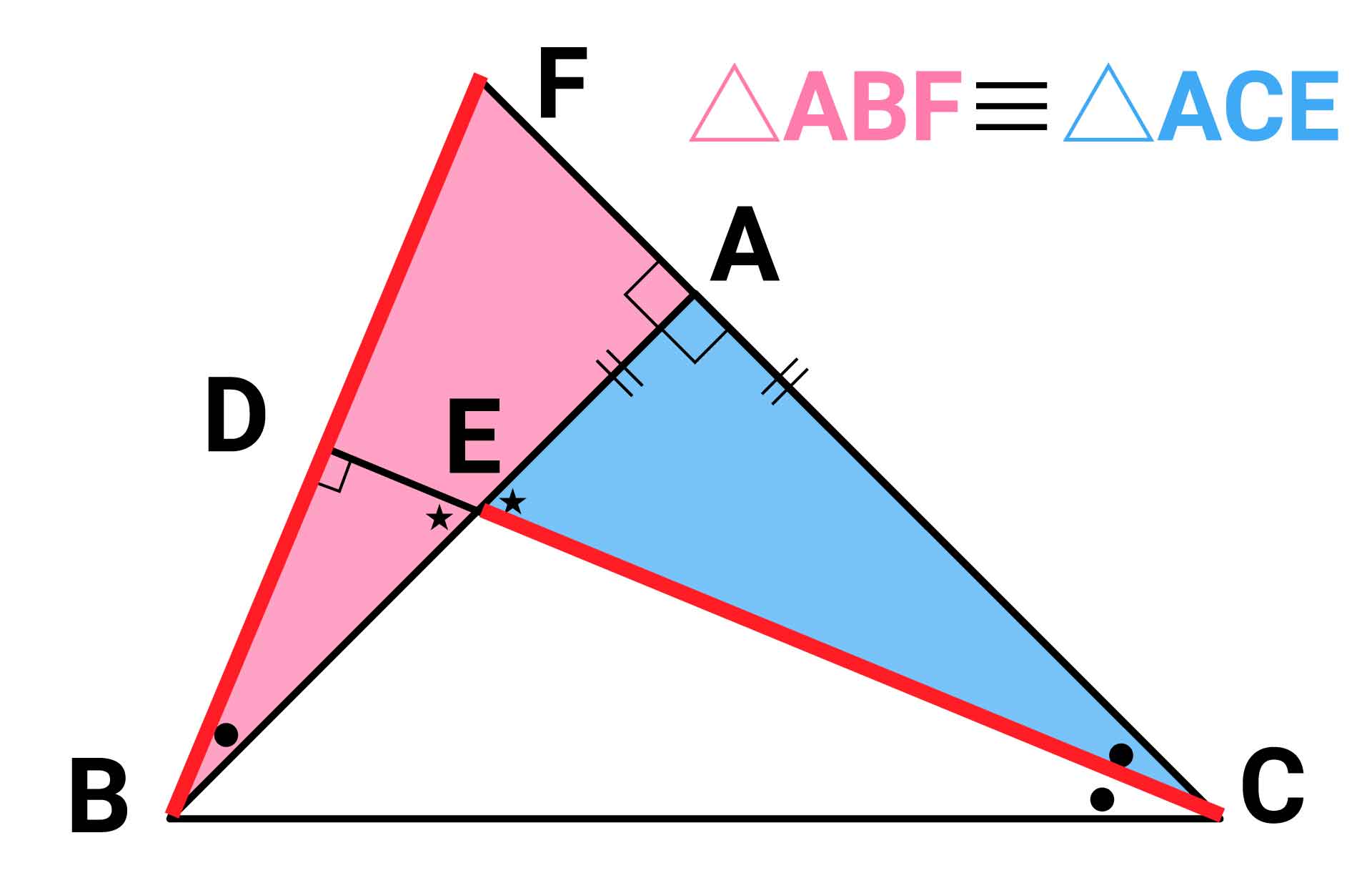
まず、三角形ABFと三角形ACEに着目します。三角形ABFと三角形ACEは、AB=ACであり、角BAF=角CAE=90度、角ABF=角ACEであることから、合同であることがわかります。
合同な図形の対応する辺の長さは等しいため、辺CEの長さは辺BFの長さと同じであることがわかります。辺BFの長さがわかれば、答えはもうすぐそこです。
ここで、三角形BCDと三角形FCDに着目します。三角形BCDと三角形FCDは、辺CDを共有しており、角BDC=角FDC=90度、角BCD=角FCDであることから、合同であることがわかります。
つまり、辺FDの長さは、対応する辺BDの長さ(6cm)と等しいため、BF=12cmです。
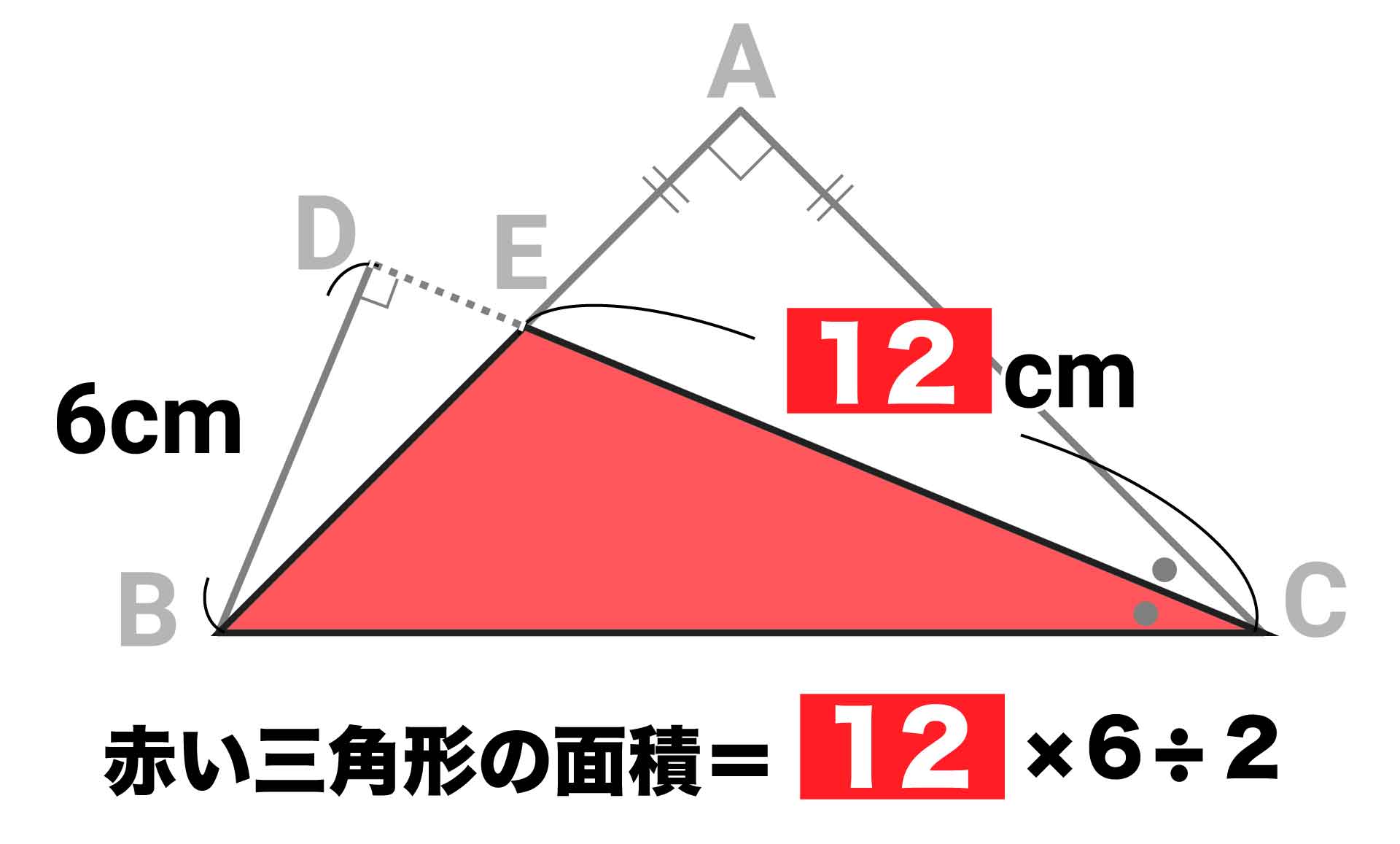
これで、CE=12cmであることがわかりました。
三角形の面積は(底辺)×(高さ)÷2で求められるので、三角形BCEの面積は12×6÷2=36cm2となります。
答え:36cm2
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】











.jpg)










.jpg)






