ヒント
このままの状態で円の面積を求めるのは難しそうです。
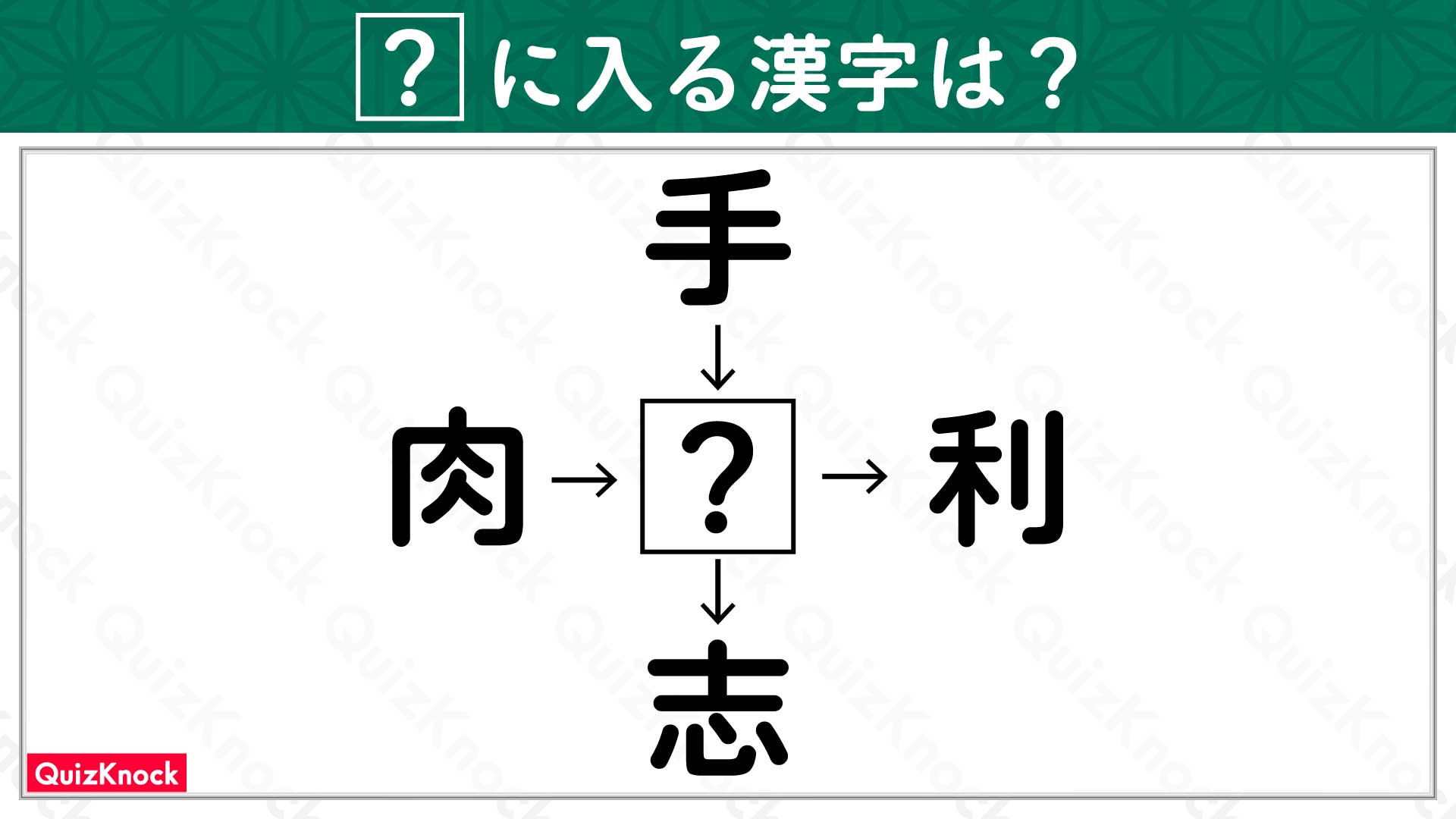
円の面積を求めるには、円の半径が必要ですよね。そこで一度、円の中心をOとして、円の半径の補助線を引いてみましょう。
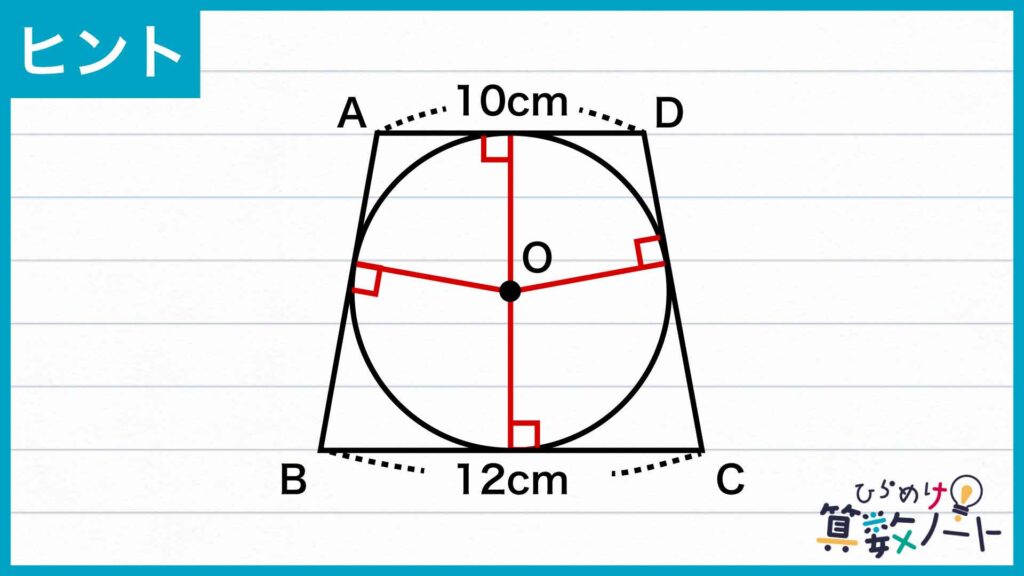
円の接線は、接点を通る半径に垂直になります。このままでも円の半径を求めるのは難しそうなので、さらにこのような補助線を引いてみます。
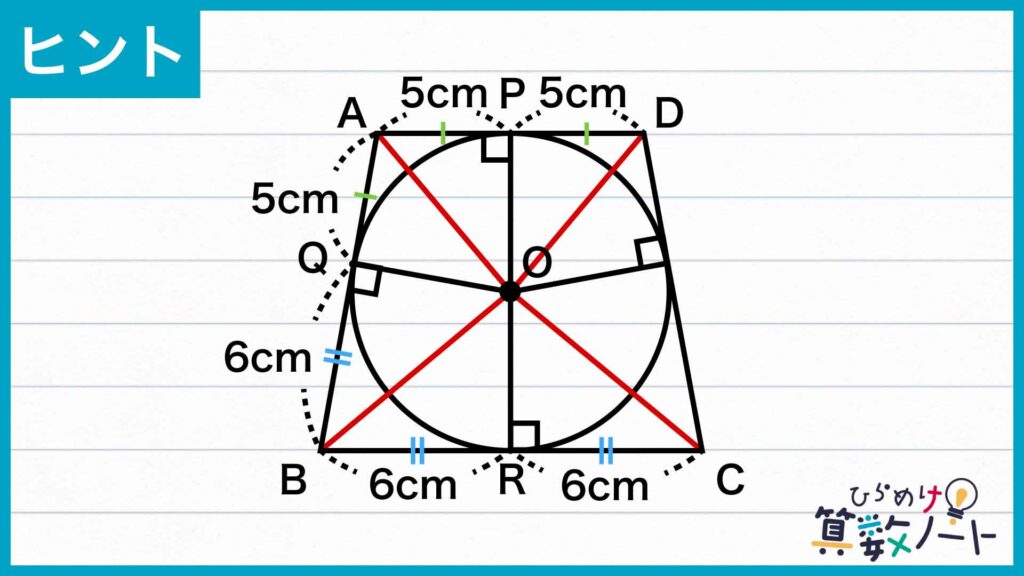
すると、複数の三角形が見えてきました。台形と円の接点を上から反時計回りにP、Q、Rと置きます。
円外の1点(台形の任意の頂点)から引いた2本の接線(台形の辺)について、円外の1点から接点までの長さが等しくなるため、AP=AQ、BQ=BRであることがわかります。
また、等脚台形の性質からAP=PD、BR=RCでもあるため、AP=PD=AQでありそれぞれ5cm、BR=RC=BQでありそれぞれ6cmとなります。
また、OP、OQ、ORはそれぞれ円の半径なので、OP=OQ=ORです。さらに、△APOと△AQO、△BQOと△BROについて、それぞれAOとBOが共通しています。
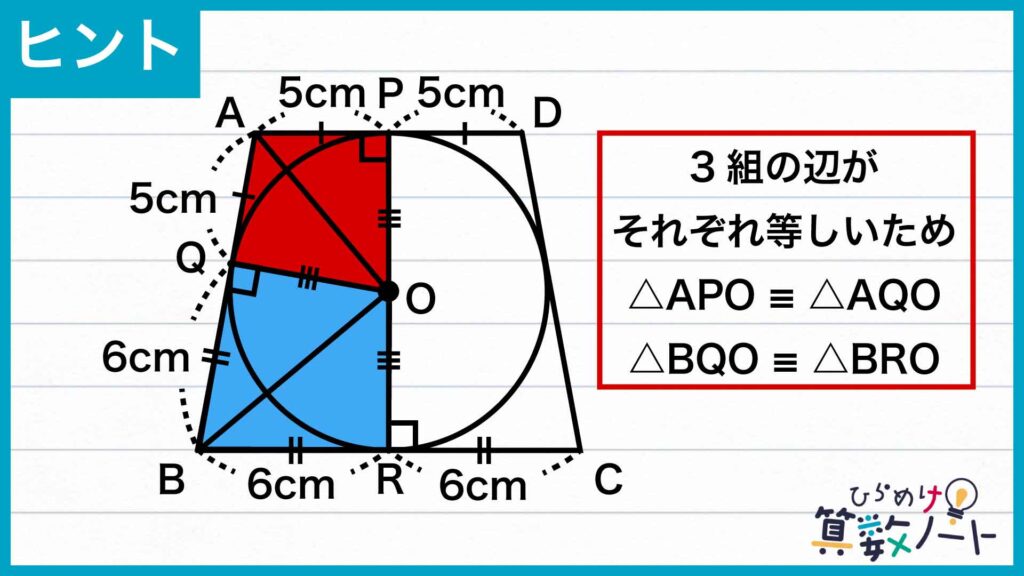
以上のことから、3組の辺の長さがそれぞれ等しいため、△APOと△AQO、△BQOと△BROはそれぞれ合同であることがわかります。



















.jpg)