問題はこちら
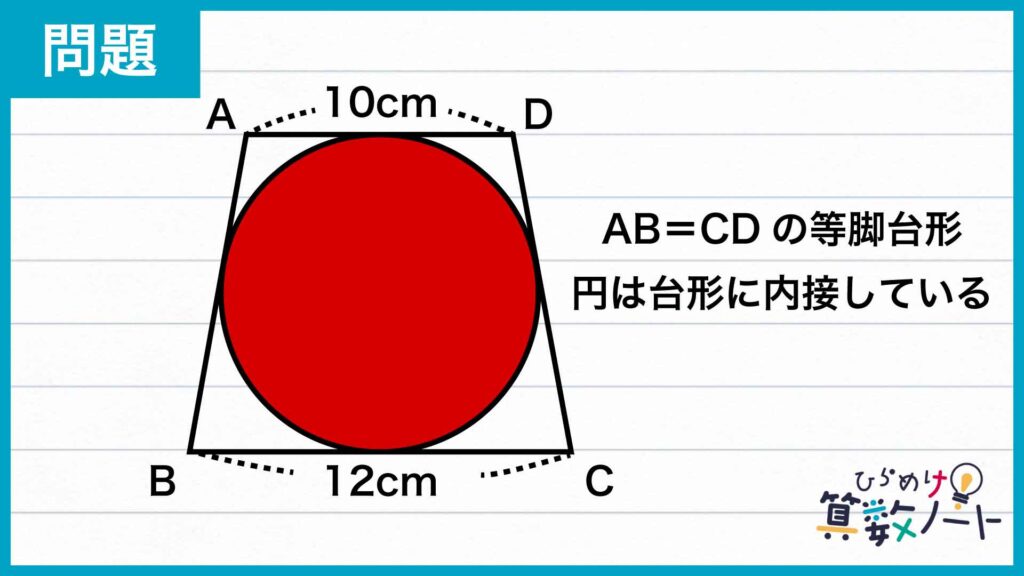
1ページ目:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつをご紹介します。
今回の問題の解き方をまとめた図がこちらになります。
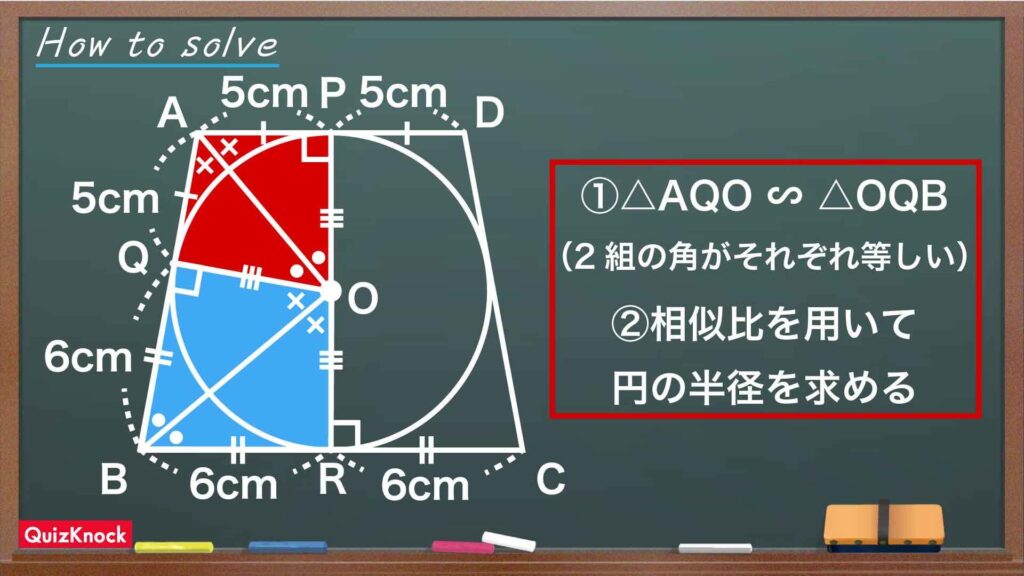
ポイントは、相似な三角形を利用して円の半径を求めることです。これを踏まえて解いていきましょう!
補助線を引く
最終的に求めたい円の面積は、円の半径がわかれば求めることができます。
そこで一度、円の半径の補助線を引いてみましょう。あわせて、台形の各辺が円の接線になっている性質を利用できる補助線も引いてみます。
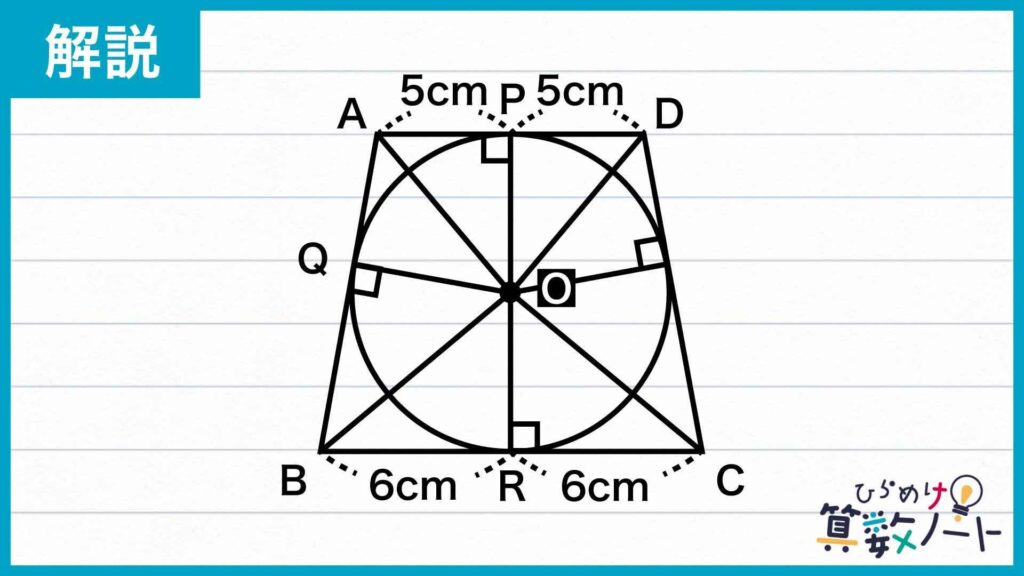
上の図のように円の中心をO、台形の各辺と円との接点をそれぞれP、Q、Rと置きます。
円外の1点(台形の任意の頂点)から引いた2本の接線(台形の辺)について、円外の1点から接点までの長さが等しくなるため、AP=AQ、BQ=BRであることがわかります。
また、等脚台形の性質からAP=PD、BR=RCでもあるため、AP=PD=AQでありそれぞれ5cm、BR=RC=BQでありそれぞれ6cmとなります。
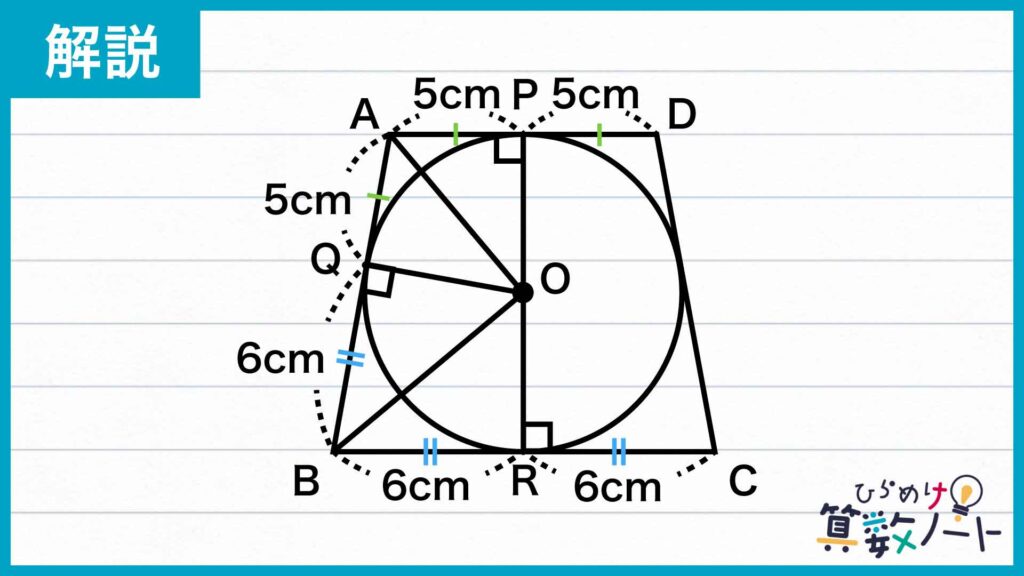
また、OP、OQ、ORはそれぞれ円の半径なので、OP=OQ=ORです。さらに、△APOと△AQO、△BQOと△BROについて、それぞれAOとBOが共通しています。
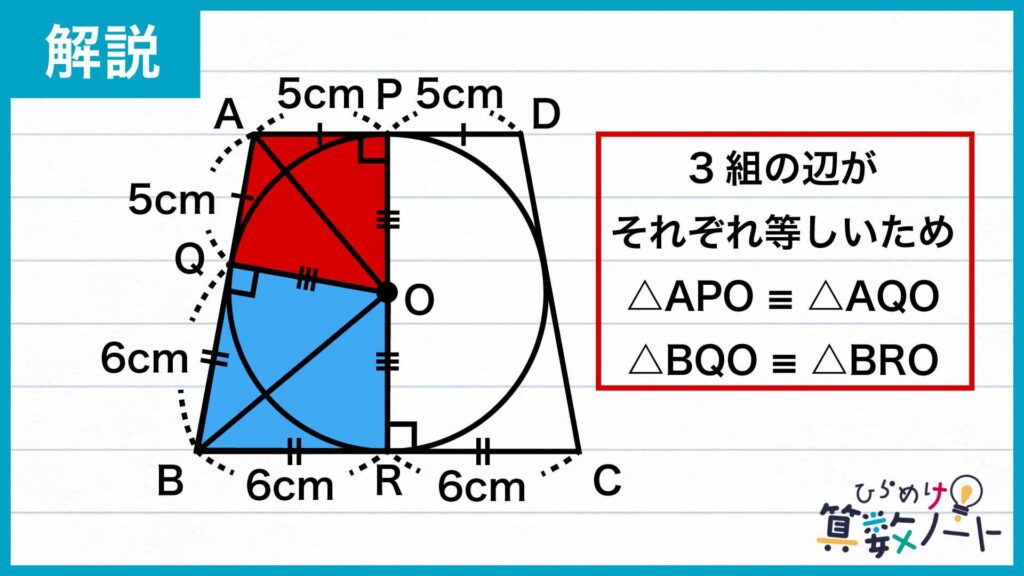
以上のことから、3組の辺の長さがそれぞれ等しいため、△APOと△AQO、△BQOと△BROはそれぞれ合同であることがわかります。
合同な三角形を利用する
△BQOと△BROは合同なので、∠QBO=∠RBO、∠BOQ=∠BORです。また、△APOと△AQOも合同なので、∠PAO=∠QAO、∠AOP=∠AOQになります。
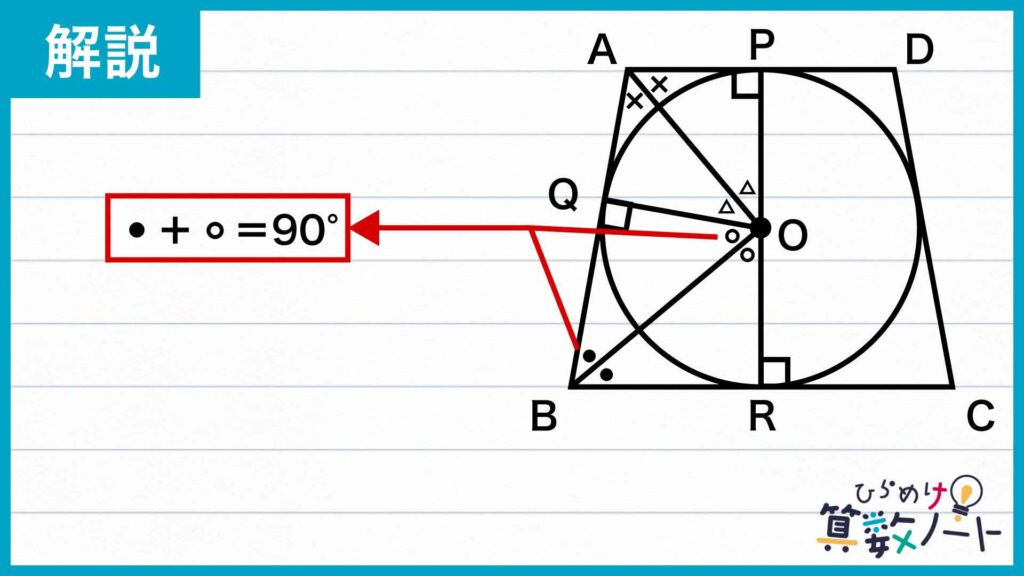
△QBOについて、三角形の内角の和から∠BQOを引くと、180-90=90°で、∠QBO+∠QOB=90°…①であることがわかります。
また、PRは直線なので、∠POR=180°です。
∠POR=∠POA+∠AOQ+∠QOB+∠BOR=180°なので、∠AOQ+∠QOB=90°…②となります。
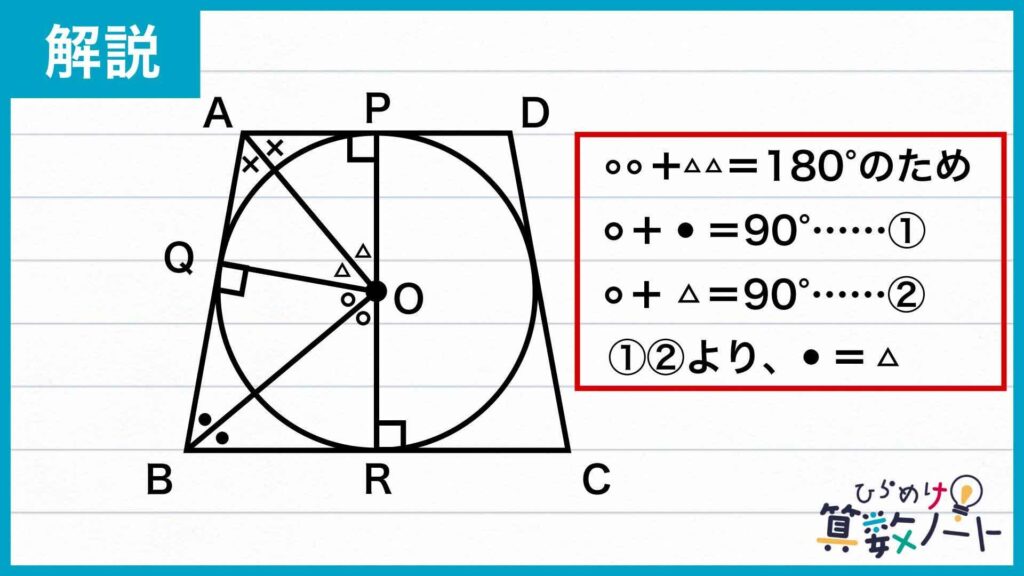
①と②より、∠QBO=∠AOQであることがわかります。このことから、∠QOB=∠QAOであることもわかります。よって、角度はそれぞれ下の図のように表すことができます。
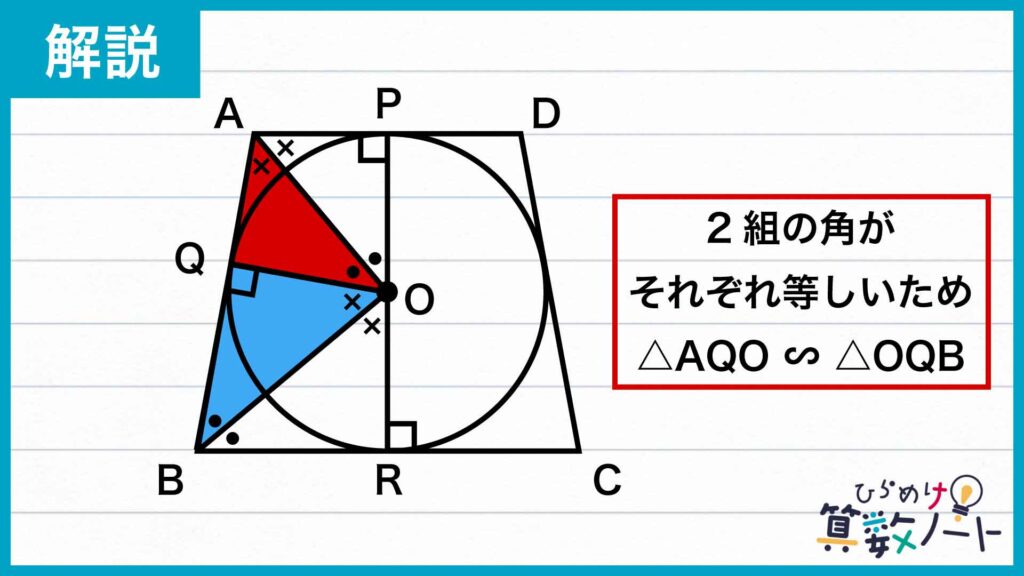
2組の角がそれぞれ等しいため、△AQOと△OQBは相似であることがわかります。
相似な三角形を利用する
ここで、求めたい円の半径をrと置きます。先ほどの過程でAQは5cm、QBは6cmであることがわかっていますね。
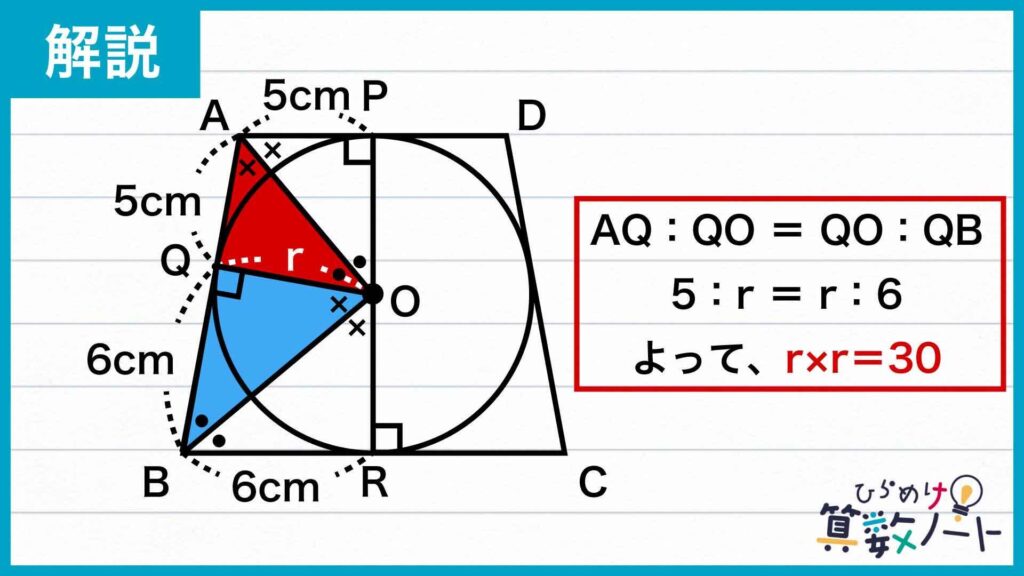
△AQOと△OQBは相似なので、AQ:QO=OQ:QBであることがわかります。これを利用して、5:r=r:6と置くことができます。比は内項の積と外項の積が等しくなるので、この式を解くとr×r=30となります。
円の面積は、半径×半径×πによって求まるので、30×π=30πcm²となります。
答え:30πcm²それではまた次の算数ノートでお会いしましょう。
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】